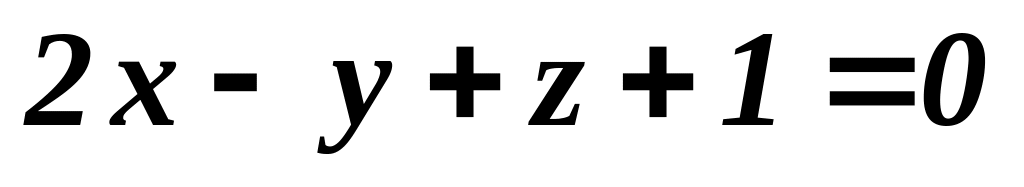Вариант № 1

1. В  АВС, где А(0;–1), В(2;1), С(1;2) найти:

   1. уравнение прямой L₁, проходящей через точки А и В;

   2. уравнение прямой L₂  L₁ и проходящей через точку С;

   3. уравнение прямой L₃ L₁ и проходящей через точку С;

   4. точку пересечения прямых L₁ и L₂.

2. Привести уравнение 4х²+8х–9y²–72у=464 к каноническому виду. Определить тип кривой и сделать чертёж.

3. Даны точки А(–1;2) и В(2;1). На оси абсцисс найти точку М(х;0), чтобы прямые L₁=AM и L₂=ВМ были перпендикулярны. Записать уравнения L₁ и L₂.

4. Для точек A (2; 1; 1) , B (1; 0; 1) , C (0; 1; 2) , D (1; 2; 0) найти:

1. уравнение прямой L₁, проходящей через точки A и D;

2. уравнение плоскости P₁, проходящей через точки A, B, C;

3. угол между прямой L₁ и плоскостью P₁;

4. уравнение прямой L₂ , проходящей через точку D перпендикулярно плоскости P₁;

5. точку пересечения прямой L₂ с плоскостью P₁.

5. Записать уравнение плоскости, проходящей через параллельные прямые L₁ : 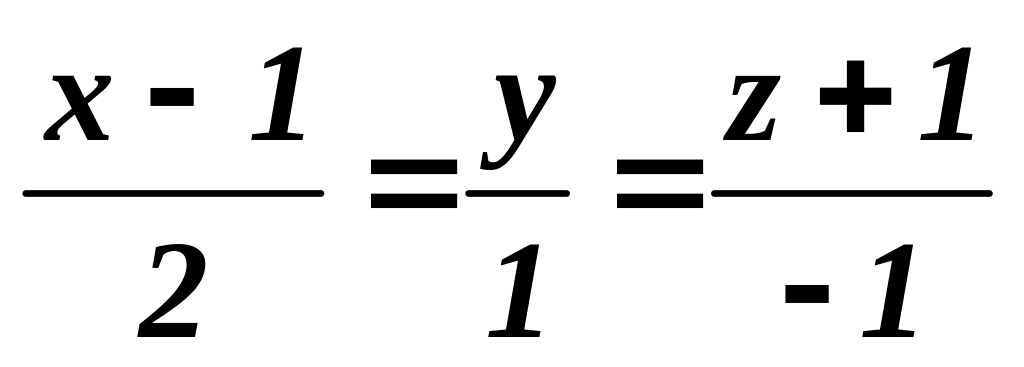и L₂ :

6. Найти точку пересечения прямых L₁ : и L₂ : .

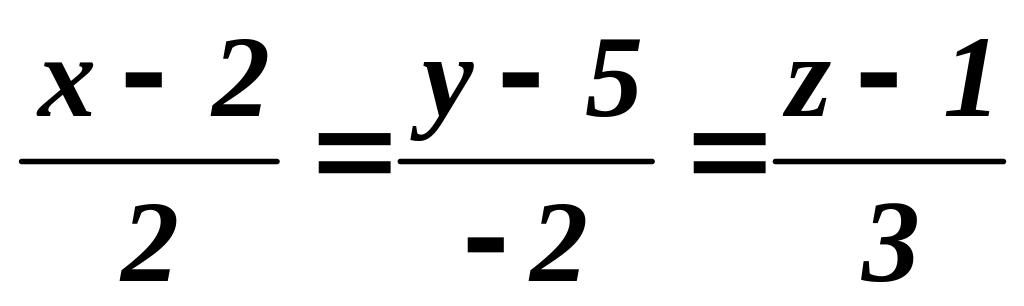Вариант № 2

1. В  АВС, где А(1,2), В(4,2), С(3,–2) найти:

1. уравнение прямой L₁, проходящей через точки А и В;

2. уравнение прямой L₂  L₁ и проходящей через точку С;

3. уравнение прямой L₃ L₁ и проходящей через точку С;

4. точку пересечения прямых L₁ и L₂.

2. Привести уравнение 9х²+25y²+18х–100у–116=0 к каноническому виду. Определить тип кривой и сделать чертёж.

3. Даны 2 вершины  АВС: А(–4,4), В(4,–12) и точка D(4,2) пересечения его высот. Найти вершину С.

4. Для точек A (3; –1; 0) , B (1; 0; 1) , C (1; 2; 1) , D (0; 1; 2) найти:

1. уравнение прямой L₁, проходящей через точки A и D;

2. уравнение плоскости P₁, проходящей через точки A, B, C;

3. угол между прямой L₁ и плоскостью P₁;

4. уравнение прямой L₂ , проходящей через точку D перпендикулярно плоскости P₁;

5. точку пересечения прямой L₂ с плоскостью P₁.

5. Найти уравнение плоскости, проходящей через точку M₁ (1; 3; 1) перпендикулярно прямой L : 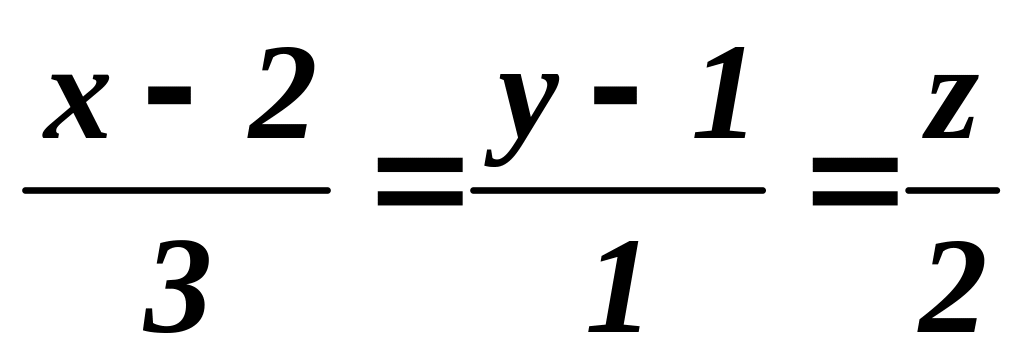. Найти точку пересечения P и L.

6. Найти уравнение плоскости, проходящей через точку M₀ (–2; 1; 1) параллельно оси 0Z и пересекающей ось 0Y при y = 2.

Вариант № 3

1. В  АВС, где А(1;1), В(–1;2), С(–1;–1) найти:

   1. уравнение прямой L₁, проходящей через точки А и В;

   2. уравнение прямой L₂  L₁ и проходящей через точку С;

   3. уравнение прямой L₃ L₁ и проходящей через точку С;

   4. точку пересечения прямых L₁ и L₂.

2. Привести уравнение 4х²+у²+16х–2у=11 к каноническому виду. Определить тип кривой и сделать чертёж.

3. Даны уравнения высот  АВС: х+у–1=0, 2х–у+1=0 и координаты его вершины В(1;1). Записать уравнения сторон АВ и ВС треугольника.

4. Для точек A (3; 2; 1) , B (1; 2; 3) , C (0; 1; 0) , D (0; 1; 1) найти:

1. уравнение прямой L₁, проходящей через точки A и D;

2. уравнение плоскости P₁, проходящей через точки A, B, C;

3. угол между прямой L₁ и плоскостью P₁;

4. уравнение прямой L₂ , проходящей через точку D перпендикулярно плоскости P₁;

5. точку пересечения прямой L₂ с плоскостью P₁.

   5. Найти точку пересечения и косинус угла между плоскостью P : 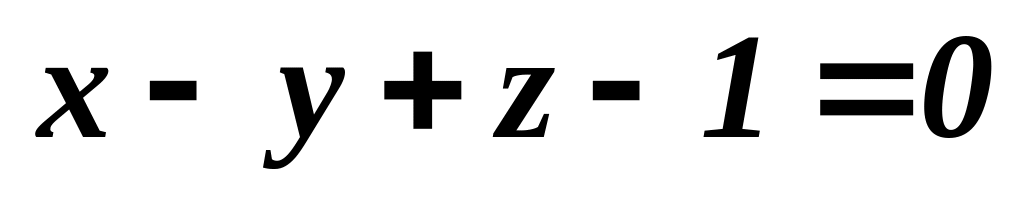и прямой

L :

5. Найти уравнение плоскости P, проходящей через точки O (0; 0; 0) , M₁ (1; 2; 3) и перпендикулярно плоскости P₁ :

­­­­­­­­­­