Решение.

1)

а) так как представлены показатели за периоды времени (за год), данный ряд динамики является интервальным,.

б) средний уровень интервального ряда определяется по формуле средней арифметической простой:

в) Рассчитаем базисные и цепные показатели ряда динамики. Базисные показатели рассчитываются в сравнении с первым годом, цепные – в сравнении с предыдущим годом по формулам:

Показатель	Базисный	Цепной
Абсолютный прирост (iбаз и iцеп)	Уi–У1	Уi–Уi-1
Темп роста (Т р)	Уi: У1 *100	Уi:Уi-1 *100
Темп прироста (Тпр)	Тр-100	Тр-100
Абсолютное значение одного процента прироста	У0(1):100	Уi-1:100

Аналитические показатели ряда динамики представим в таблице.

Таблица 2.1 Анализ динамики среднедушевого дохода на душу населения

Год	Среднедушевые доходы руб./чел.	Абсолютный прирост, руб./чел.		Темп роста, %			Темп прироста, %			Абсолютное значение 1% прироста, руб./чел.
		цепной	базисный		цепной	базисный		цепной	базисный
А	1	2	3		4	5		6	7		9
2006	8628	-	-		100	100		-	-		-
2007	10734	2394	2394		123,4	123,4		23,4	23,4		102,14
2008	13886	2372	4766		118,8	146,7		18,8	46,7		126,08
2009	15435	2058	6824		113,7	166,8		13,7	66,8		149,8
2010	17128	1755	8579		110,3	184,0		10,3	84,0		170,38

2. Средний абсолютный прирост можно рассчитать:

где - последний уровень ряда;

- первый уровень ряда;

- число уровней ряда.

Среднегодовой темп роста определяется

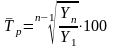
где п- число уровней ряда.

или 116,5%

Средний темп прироста

Можно сделать следующие выводы о динамике среднедушевых доходов на душу населении.Среднедушевые доходы увеличивались год от года. За 5 лет они увеличились на 8579 руб./чел. или на 84%.. Среднегодовой показатель среднедушевого дохода за 5 лет составил 14726,60 руб./чел., а среднегодовой прирост 2144,75 руб./чел., или 16,5%.

3)

Определим линейную форму тренда среднедушевых доходов населения

В виде модели примем уравнение прямой

Y_t=a₀+a₁t.

где Y_t - значения выравненного ряда;

t - показатель времени (месяцы, годы, и т.д.);

а₀, и a₁ - параметры прямой, определенные из системы нормальных уравнени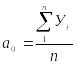й:

; и

Расчеты проведем с помощью таблицы

Год	Среднедушевые доходы руб./чел., у	t	t2	yt	Теоретический уровень
1	2	3	4	5	6
2006	8628	-4	16	-40856	10409
2007	10734	-2	4	-25216	12567,8
2008	13886	0	0	0	14726,6
2009	15435	+2	4	34076	16885,4
2010	17128	+4	16	75172	19044,2
Итого	73633	0	40	43176	73633

а₀ = 73633/5 = 14726,60 руб./чел.

а₁ = 43176/40 = 1079,40 руб./чел.

Y= 14726,60+1079,40*t

Теоретические ряды проставим в таблице.

Построим график динамики среднедушевых доходов населения за изучаемый период по фактическим и теоретическим данным.

Видим, что фактические и теоретические данные практически одинаковые.

Спрогнозируем среднедушевые доходы населения на 2013 год, используя методы:

1. среднего абсолютного прироста:

У₂₀₁₃ = 18552,6 + 2089,15*3 = 24820,05 руб./чел.

2. среднего тема роста:

У₂₀₁₃ = 18552,6*1,161³ = 29033,64 руб./чел.

3. аналитического выравнивания:

Y = 14626,04+1047,44*10 = 25100,44 руб./чел.

Видим, что прогнозные значения на 2013 год, рассчитанное способом среднего абсолютного прироста и способом аналитического выравнивания, приближены друг к другу, а значение, рассчитанное способом среднего темпа роста, отличается.

Рис. 2.1 Динамика среднедушевых доходов населения за 2006-2010 г.г.

Задача 3. В 2009 г. среднегодовая численность населения города составляла 1018,3 тыс. чел, в 2010 г. – 1025, 8 тыс. чел, в 2011 г. – 1030, 6 тыс. чел.

1. Определить в % базисные относительные величины динамики (с точностью до 0,1 %):

а) 102,8 и 101,2; в) 100,7 и 101,2 с) 101,8 и 102,3.

2) Определить в % цепные относительные величины динамики (с точностью до 0,1 %):

а) 105,3 и 101, 8; в) 100,7 и 100,5; с) 100,7 и 102,4.

Решение.

Базисные относительные величины динамики – темпы роста определяются по формуле: . Тогда , .

Цепные относительные величины динамики – темпы роста определяются по формуле: 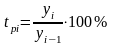. Тогда , .

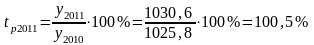Задача 4. Дисперсия признака равна (с точностью до 0,1) при условии: средняя величина признака – 22 тыс. руб., коэффициент вариации – 26%:

а) 44,5 с) 12,8

в) 32,7 d) 37,2

Решение.

Задача 5. Цены на бензин в 4м квартале текущего года по сравнению с 4-м кварталом предыдущего года возросли на 1 литр с 23 до 27 руб. Каков ежеквартальный темп прироста цен на бензин (в %):

а) 8,3 с) 2,9

в) 4,1 d) 10,4

Решение.

Коэффициент роста за весь период , средний темп роста за квартал: , тогда ежеквартальный темп прироста цен на бензин составил 104,1-100 = 4,1%.

Вариант 6