Задача 1. Имеются выборочные данные (выборка 5%-ная механическая) по 26 предприятиям за отчетный год:

Номер предприятия	Среднегодовая стоимость ОПФ, млн. руб.
3	870
4	1210
5	1150
6	925
7	1630
8	1390
9	730
10	975
11	890
12	905
13	430
14	830
15	920
16	1100
17	970
18	700
19	810
20	780
21	1250
22	930

По исходным данным Вашего варианта:

1. Постройте статистический ряд распределения, образовав 5 групп с равными интервалами. Построить графики ряда распределения: гистограмму, полигон, кумуляту.

2. По каждой группе и совокупности предприятий определить число предприятий и их удельный вес в общем количестве предприятий (структуру). Результаты расчетов представьте в таблицы.

3. По данным группировки рассчитайте характеристики ряда распределения предприятий: средний уровень ряда (по формулам средней арифметической обычным методом и методом моментов); размах вариации; среднее линейное отклонение; дисперсию (по формулам обычным методом и методом моментов); среднее квадратическое отклонение; коэффициент вариации; моду и медиану для дискретного и интервального ряда распределения. Проанализировать полученные результаты.

4. С вероятностью 0,964 определить ошибку выборки средней величины на одно предприятие и границы, в которых будет находиться генеральная средняя.

С вероятностью 0,997 определите ошибку выборки для доли предприятий, находящихся в последней 5-ой группе интервального ряда распределения и границы, в которых будет находиться генеральная доля. Сделайте выводы.

Решение.

1. Определим величину интервала группировки 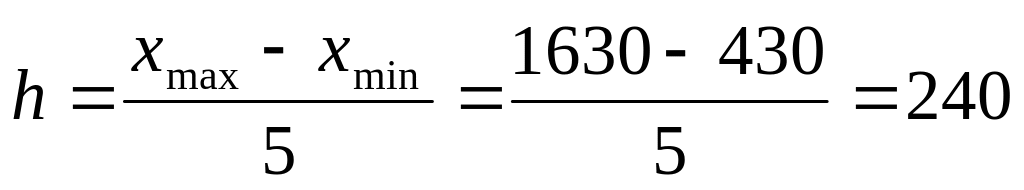млн.руб.

Тогда статистический ряд примет вид:

Среднегодовая стоимость ОПФ, млн. руб.	Число предприятий	Накопленные частоты
430-670	1	1
670-910	8	9
910-1150	6	15
1150-1390	3	18
1390-1630	2	20
Итого	20

Изобразим полученный ряд графически.

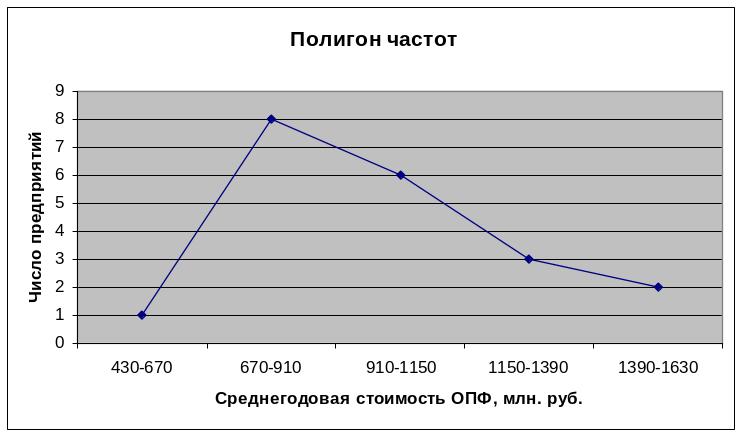
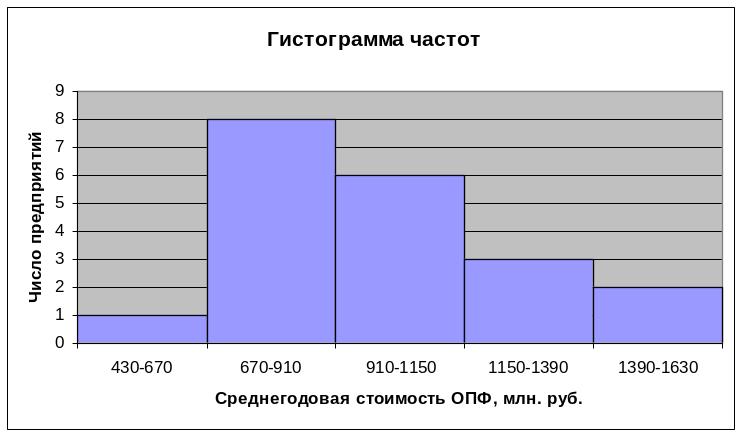
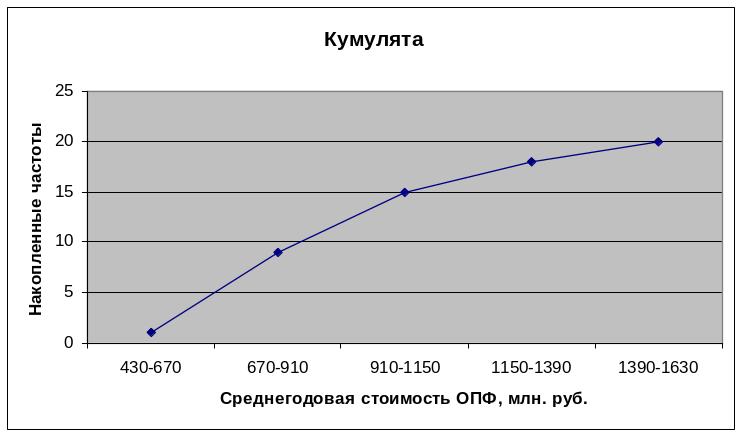
2. Рассчитаем относительные показатели структуры = Часть совокупности * 100% / Итог совокупности.

Среднегодовая стоимость ОПФ, млн. руб.	Число предприятий	Структура, %
430-670	1	5,0
670-910	8	40,0
910-1150	6	30,0
1150-1390	3	15,0
1390-1630	2	10,0
Итого	20	100

3) Средний уровень ряда ищем по формуле средней арифметической взвешенной , где в качестве вариант используем середины интервалов.

Среднегодовая стоимость ОПФ, млн. руб.	Число предприятий,	Середины интервалов,
430-670	1	550	550
670-910	8	790	6320
910-1150	6	1030	6180
1150-1390	3	1270	3810
1390-1630	2	1510	3020
Итого	20		19880

млн.руб.

Найдем средний уровень ряда по методу моментов.

Среднегодовая стоимость ОПФ, млн. руб.		х	х-А
430-670	1	550	-240	-1	-1
670-910	8	790	0	0	0
910-1150	6	1030	240	1	6
1150-1390	3	1270	480	2	6
1390-1630	2	1510	720	3	6
Итого	20				17

млн.руб.

Размах вариации млн.руб.

Среднее линейное отклонение .

Среднегодовая стоимость ОПФ, млн. руб.	Число предприятий,	Середины интервалов,
430-670	1	550	444	444
670-910	8	790	204	1632
910-1150	6	1030	36	216
1150-1390	3	1270	276	828
1390-1630	2	1510	516	1032
Итого	20			4152

млн.руб.

Определим дисперсию обычным способом по формуле .

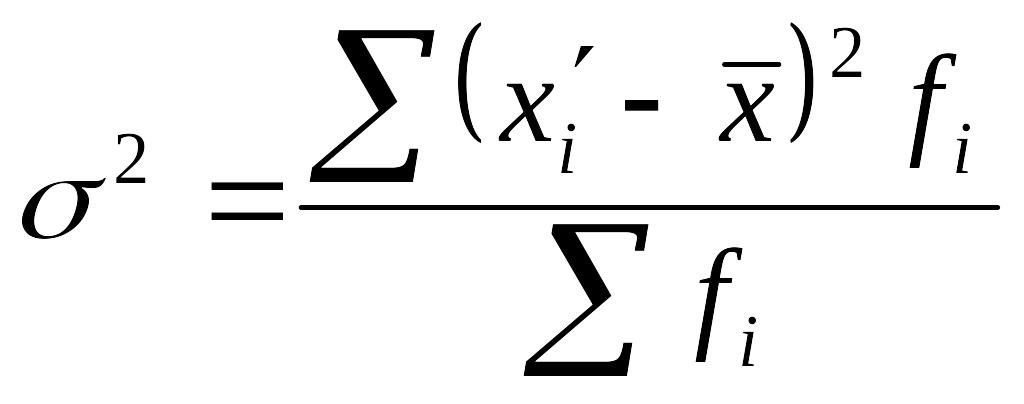Среднегодовая стоимость ОПФ, млн. руб.
430-670	1	550	197136	197136
670-910	8	790	41616	332928
910-1150	6	1030	1296	7776
1150-1390	3	1270	76176	228528
1390-1630	2	1510	266256	532512
Итого	20			1298880

Определим дисперсию упрощенным методом, т.е. используя способ моментов.

Себестоимость единицы продукции, руб.		х	х-А
430-670	1	550	-240	-1	1	1
670-910	8	790	0	0	0	0
910-1150	6	1030	240	1	1	6
1150-1390	3	1270	480	2	4	12
1390-1630	2	1510	720	3	9	18
Итого	20					37

Среднее квадратическое отклонение млн.руб.

Коэффициент вариации . Т.к. коэффициент вариации меньше 33%, то исследуемую совокупность можно считать однородной.

Мода в дискретном ряду – наиболее частое значение, в нашем случае все значения встречаются по одному разу.

Медиана в дискретном ряду – значение, стоящее в центре ряда распределения, в нашем случае – (920+925)/2 = 922,5 млн.руб.

Найдем моду, для этого сначала найдем модальный интервал, т.е. интервал с наибольшей частотой (выделен желтым цветом в таблице). Чтобы найти конкретное значение моды, необходимо использовать формулу

где x_Мо - нижняя граница модального интервала; i_Мо - величина модального интервала; f_Мо - частота модального интервала; f_Мо-1 - частота интервала, предшествующего модальному; f_Мо+1 - частота интервала, следующего за модальным.

млн.руб.

Найдем медиану, для этого сначала найдем медианный интервал, т.е. первый интервал, где сумма накопленных частот превышает половину наблюдений от общего числа всех наблюдений. В нашем случае он не совпадает с модальным интервалом. Численное значение медианы обычно определяют по формуле

где: - нижняя граница медианного интервала;

- величина медианного интервала;

- накопленная частота интервала, предшествующего медианному;

- частота медианного интервала;

млн.руб.