2. Автокорреляционная функция сигнала

С преобразованием Фурье сигнала связана автокорреляционная функция сигнала (АКФ). Когда мы интересуемся корреляцией двух явлений, спрашиваем, насколько близко они соотносятся по поведению или виду и насколько они совпадают. В математике автокорреляционная функция сигнала во временной области описывает соответствие сигнала самому себе, смещенному на некоторый промежуток времени.

Для периодического сигнала для (2.23)

Функция автокорреляции – это функция разности времен между сигналом и его смещаемой по оси времени копией.

Свойства функции автокорреляции:

1. Симметрия по относительно нуля

2. Максимальное значение в нуле

3. АКФ и энергетическая спектральная плотность сигнала являются Фурье-образами друг друга

4. Для энергетического сигнала значение АКФ в нуле равно энергии сигнала

5. Для периодического сигнала значение АКФ в нуле равно средней мощности сигнала

Мы последовательно перемещаем копию в положительном направлении временной оси и задаем в каждый момент времени вопрос, насколько исходная версия и копия сигнала соответствуют друг другу. Время рассматривается как параметр сканирования. Автокорреляционная функция может дать представление о ширине спектра сигнала. Предположим, что копия сигнала перемещается вдоль оси времени очень медленно. Это значит, что сигнал имеет малую ширину полосы, тогда автокорреляционная функция будет иметь широкую форму. Если копия сигнала перемещается вдоль оси времени быстро (большая скорость передачи сигнала и, соответственно, ширина полосы), то автокорреляционная функция будет иметь узкую форму. Коэффициент корреляции – значение функции корреляции в данный момент времени.

Рассмотрим случай =1, соответствующий наилучшей корреляции сигналов и в течение времени передачи символа. Если сигналы рассматривать как векторы, угол между ними будет равен нулю. В реальной системе цифровой связи сигналы (элементы алфавита) должны быть максимально несопоставимы, чтобы их можно было легко различать (обнаруживать). Частный случай =-1 соответствует «антикорреляции» и в течение времени передачи символа. Угол между векторами сигналов в этом случае составляет 180⁰, а сигналы называются антиподными. Случай =0, соответствующий нулевой корреляции между сигналами и , можно интерпретировать как угол 90⁰ между векторами сигналов. В этом случае сигналы называются ортогональными. Чтобы сигналы были ортогональными, они не должны коррелировать в течение времени передачи символа, т.е. должно выполняться условие:

(2.24)

Задача

Покажите, что три функции, приведенные на рисунке 2.10, попарно ортогональны на интервале (-2;2).

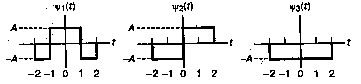
Рисунок 2.10

Решение

Проверим попарную ортогональность сигналов с учетом (2.24).

2. Импульсная характеристика

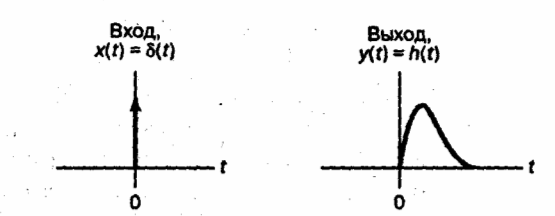
Линейная, инвариантная относительно времени система или сеть, показанная на рисунке 2.11, описывается во временной области импульсной характеристикой h(t), представляющей собой реакцию системы при подаче на ее вход единичного импульса ( см. рисунок 2.12)

.

h(t)

Рисунок 2.11 Линейная система и ее ключевые параметры

а) б)

Рисунок 2.12 Иллюстрация понятия «Импульсный отклик»

Задача

На рисунке 2.13 приведен пример цепи запоминания, широко используемой в импульсных системах. Определите импульсную характеристику этого канала.

Рисунок 2.13

V(t)

Рисунок 2.14

Решение

На рисунке 2.14 показан входной сигнал х(t) , задержанный относительно него второй сигнал x(t+t₀) и сигнал рассогласования v(t).Интегратор представим линейной, инвариантной (неизменной) относительно времени системой, которая характеризуется импульсной характеристикой h(t) ( реакция системы при подаче на ее вход единичного импульса), которая изображена на рисунке 2.15,а. Отклик системы на произвольный сигнал v(t), поданный на ее вход, является сверткой v(t) c h(t), что записывается следующим образом:

(2.25)

Независимой переменной в интеграле свертки является . На рисунке 2.15,б показаны bceu функции v( ) и h(- ). Функция h(- ) получается отображением h( ) относительно оси =0. Член h(t- ) представляет функцию h(- ), смещенную на t секунд вдоль положительного направления оси . На рисунке 2.15,в показана функция h(t₁- ). Значение интеграла свертки в момент времени t=t₁ вычисляем как площадь под кривой произведения v( ) на h(t₁- ) ( см. рисунок 2.15,г). Интеграл свертки в момент t=t₂ равен заштрихованной области на рисунке 2.15,д. На рисунке 2.15,е приведен график отклика i(t) на выходе схемы при квадратном импульсе на входе. Каждое вычисление интеграла свертки для некоторого момента времени t_i дает одну точку i(t_i) графика на рисунке 2.15,е.

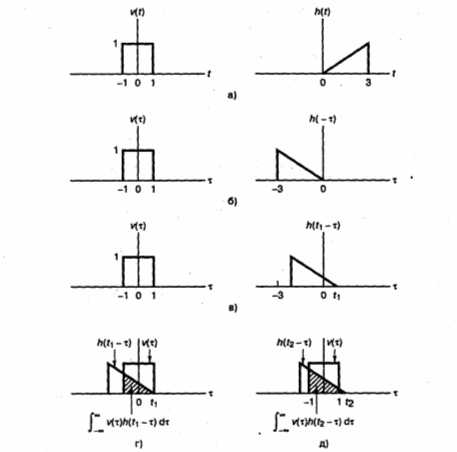
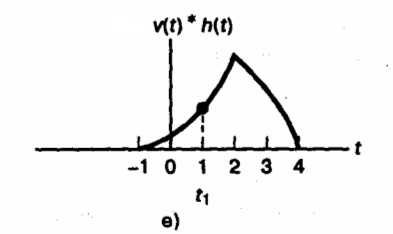
Рисунок 2.15

Лекция 3