2. Связь между скоростью передачи данных и шириной полосы

Хотя данный сигнал может содержать значительный диапазон частот, любая система связи на практике сможет вместить только ограниченную область частот. Рассмотрим прямоугольный сигнал (см. рисунок 2.7). Пусть положительный импульс представляет двоичную единицу, а отрицательный – двоичный нуль. Длительность каждого импульса равна 1/2f, следовательно, скорость передачи данных равна 2f бит/с. Из каких же гармоник составлен данный сигнал? Обратимся к рисунку 2.2, в. При сложении синусоид с частотами f и 3f получается сигнал, форма которого начинает походить на форму прямоугольного сигнала. Если продолжить этот процесс и добавить синусоидальный сигнал с частотой 5f ( рисунок 2.8), а затем – синусоидальный сигнал с частотой 7f ( рисунок 2.9), то результирующий сигнал начнет все больше и больше приближаться к прямоугольной форме.

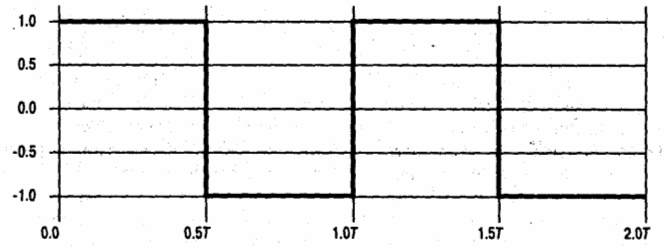
Рисунок 2.7 Прямоугольный сигнал

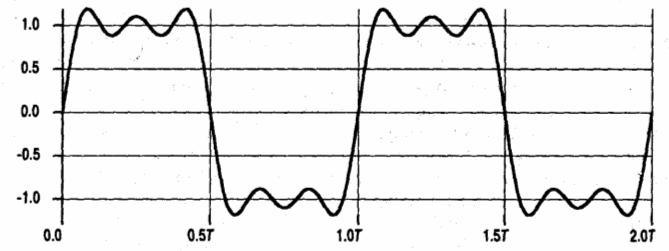
Рисунок 2.8

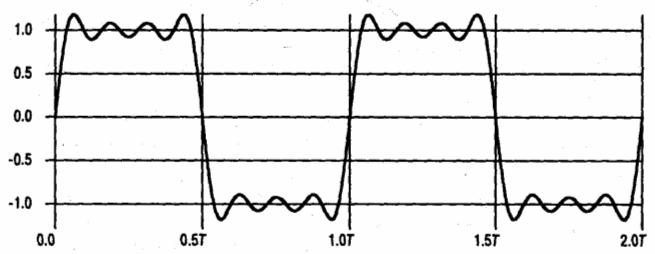
Рисунок 2.9

Гармоники прямоугольного сигнала с амплитудами А и –А можно выразить как:

(2.22)

Таким образом, сигнал содержит бесконечное число гармоник и, следовательно, имеет бесконечную ширину полосы. Однако максимальная амплитуда k-той гармоники, kf, равна всего лишь 1/k, поэтому большая часть энергии приходится на несколько первых гармоник.

Пример

Какой скорости передачи данных можно добиться в цифровой системе?

Случай 1

Аппроксимируем прямоугольный сигнал формой

(см. рисунок 2.8) . Если частоту fположить равной f=1МГц, то период собственной частоты Е=1/10⁶=1мкс, а ширина полосы сигнала равна 5-1=4 МГц. Один бит будет поступать каждые 0,5 мкс, а скорость передачи данных при этом будет 2*10⁶=2МГц.

Случай 2

Если частоту f положить равной f=2МГц, то период собственной частоты в этом случае будет равен Т=1/2*10⁶=0,5мкс, а ширина полосы сигнала равна 5*2*10⁶-1*2*10⁶=8 МГц. Один бит будет поступать каждые 0,25 мкс, а скорость передачи данных при этом будет 2*2*10⁶=4МГц. Следовательно, при равных других параметрах, удвоение ширины полосы приводит к удвоению возможной скорости передачи данных.

Случай 3

Аппроксимируем прямоугольный сигнал формой

(см. рисунок 2.2,в) . Если частоту fположить равной f=2МГц, то период собственной частоты Т=1/2*10⁶=0,5мкс, а ширина полосы сигнала равна 3*2*10⁶-1*2*10⁶=4 МГц. Один бит будет поступать каждые 0,25 мкс, а скорость передачи данных при этом будет 2*2*10⁶=4МГц. Следовательно, при данной ширине полосы могут поддерживаться различные скорости передачи данных, а зависит эта скорость от способности приемника различать 0 и 1 при наличии помех и искажений сигнала.

Таким образом, если передавать сигнал через среду, передающая система наложит ограничения на ширину полосы, которую можно передать. Кроме того, чем больше передаваемая полоса, тем выше стоимость передачи. Поэтому, с одной стороны, экономические и практические соображения подсказывают аппроксимировать цифровую информацию сигналом с ограниченной шириной полосы. С другой стороны, ограничение ширины полосы создает искажения, затрудняющие интерпретацию принимаемого сигнала (см. рисунок 2.9).

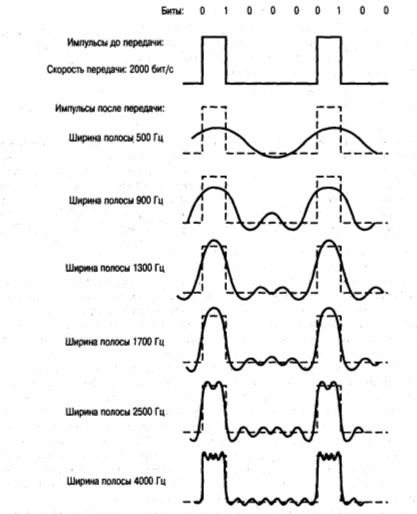
Рисунок 2.9 Влияние ширины полосы на цифровой сигнал

Чем больше ограничена полоса, тем больше потенциальная возможность возникновения ошибок при приеме. Если скорость передачи данных составляет для цифрового сигнала R бит/с, то достаточно хорошее представление сигнала можно получить при ширине полосы 2R Гц. Если полоса сигнала сосредоточена около некоторой частоты, называемой центральной частотой, то чем выше центральная частота, тем шире возможная полоса и выше потенциальная скорость передачи данных.