Цифровые фильтры
Цифровыми называются фильтры, реализованные на основе методов цифровой обработки сигналов.
Сначала
рассмотрим фильтр с конечной импульсной
характеристикой (фильтр
КИХ –
finite
impulse
response
– FIR),
схема работы которого представлена на
рисунке 4.1. Первый отсчет (назовем его
)
входной числовой последовательности
умножается на коэффициент
и появляется на выходе фильтра в виде
отсчета
.
Рисунок 4.1 Фильтр КИХ
Плечи
-
называются ветвями (tap).
В фильтре присутствует несколько линий
задержки, каждая из которых задерживает
сигнал на время Т, что соответствует
периоду цикла выборки сигнала в приемнике.
Входной импульс
достигает ветви
после задержки на один период, в это
время на входе фильтра появляется
следующий импульс
.
Следовательно, в момент времени t=0
выходной сигнал
равен произведению
.
В момент времени t=T
на выходе фильтра появляется новый
сигнал
,
который равен произведению
плюс новый входной импульс
.
Функцию
можно найти с помощью свертки функций
и
,
она называется сверточной суммой.
Для определения частотной характеристики фильтра, нужно подать на его вход сигнал с постоянной амплитудой и бесконечным частотным диапазоном, т.е. дельта-функцию. Если предположить, что коэффициенты передачи и отрицательны ( см. рисунок 4.1), тогда при поступлении на фильтр дельта-функции на его выходе появится сигнал, показанный на рисунке 4.2. По истечении интервала времени 3Т с момента подачи на вход исходного импульса сигнал на выходе фильтра вернется в нулевое положение.
Фильтр КИХ получил свое название благодаря тому, что его входной сигнал исчезает в течение N отсчетов после поступления исходного импульса на вход фильтра. Здесь N – количество элементов задержки, или ветвей фильтра. Для построения фильтрующего устройства необходима система, которая может умножать (с разными весовыми коэффициентами для каждой ветви), складывать и последовательно сохранять входные импульсы. Это можно реализовать с помощью цифрового компьютера и микропроцессора.
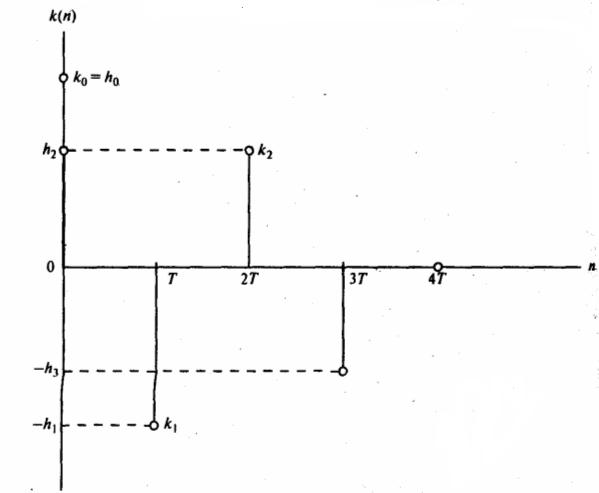
Рисунок 4.2 Импульсная характеристика фильтра КИХ
Задача
Нарисуйте импульсную характеристику фильтра КИХ, показанного на рисунке 4.3.
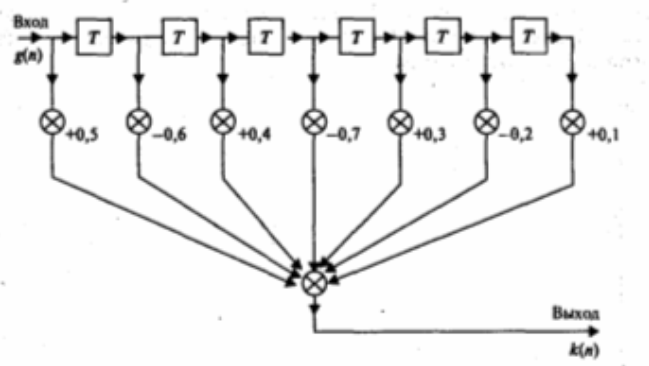
Рисунок 4.3 Структура фильтра КИХ
Решение
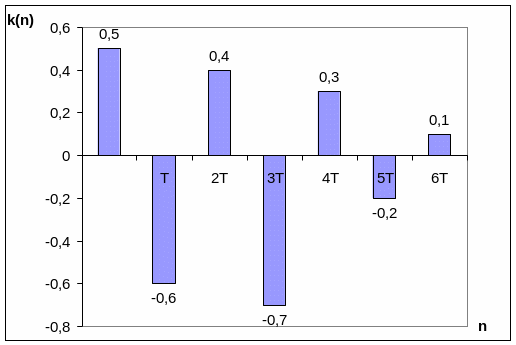
Рисунок 4.4 Импульсная характеристика фильтра КИХ
На рисунке 4.5 изображена схема работы второго типа цифрового фильтра – фильтра с бесконечной импульсной характеристикой или фильтра БИХ (finite impulse response – IIR), содержащая три ветви. Ветви в фильтре БИХ являются ветвями обратной связи (feed back) с выхода.
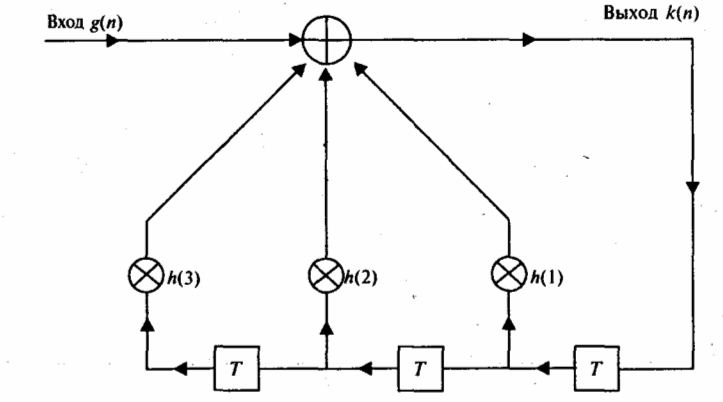
Рисунок 4.5 Фильтр с бесконечной импульсной характеристикой
Для фильтра, изображенного на рисунке 4.5, можно записать следующее выражение для выходного сигнала k(n):
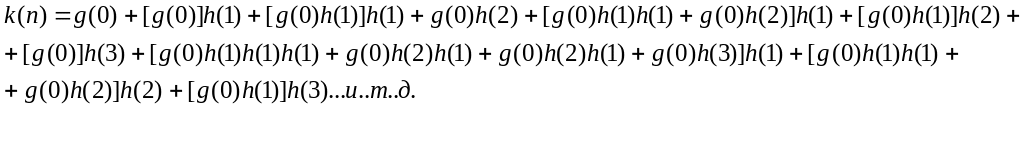(4.1)
Этот сигнал приведен на рисунке 4.6, где
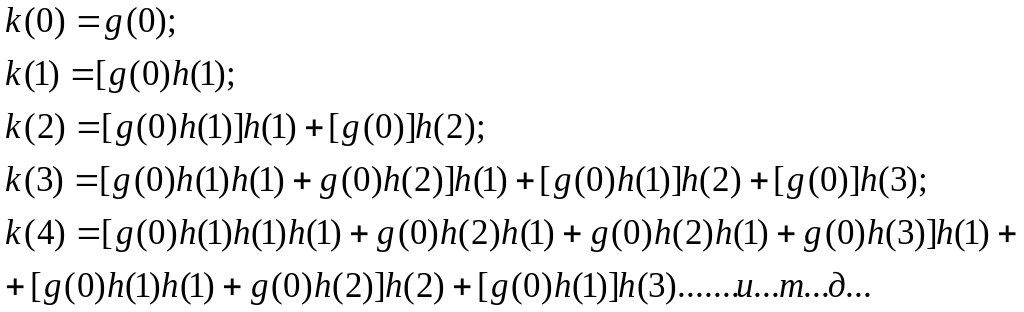
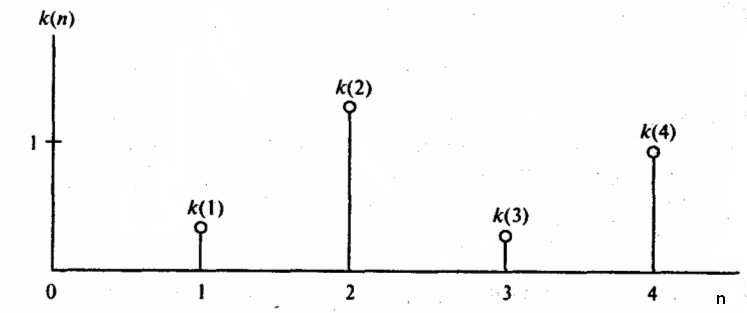
Рисунок 4.6 Сигнал на выходе фильтра БИХ
Для того, чтобы создать цифровой фильтр по заданным параметрам ( частоте среза и крутизне АЧХ) можно взять аналоговую функцию с известными характеристиками, например, полином Чебышева n-порядка. Зная его функцию передачи, можно математически (используя, скажем, z-преобразование) определить функцию передачи эквивалентного цифрового фильтра, которая будет иметь вид числовой последовательности. Теперь несложно нарисовать схему фильтра, которую можно реализовать как на логических элементах, так и программно. Однако такой подход к моделированию электронных систем связан с утомительными математическими расчетами и подвержен ошибкам. Поэтому на практике обычно применяют один из многочисленных пакетов по компьютерному моделированию систем цифровой обработки сигналов, которые сами определяют количество ветвей и их весовые характеристики по заданным техническим требованиям. При более детальном рассмотрении фильтров с БИХ можно сделать вывод, что при заданной частоте среза они имеют меньшее количество ветвей, чем фильтры с КИХ. Зато фильтры с КИХ превосходят фильтры с БИХ по качеству фазовой характеристики.
Задача
Изобразите графически импульсную характеристику фильтра с БИХ, показанную на рисунке 4.7.
Решение
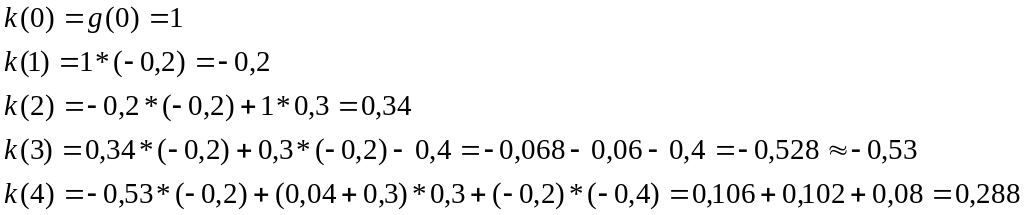
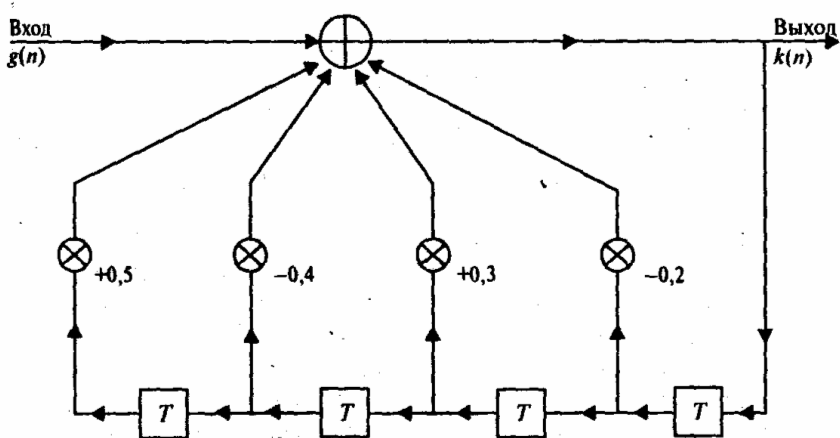
Рисунок 4.7 Схема фильтра с БИХ
По результатам расчета импульсной характеристики имеем импульсную характеристику, показанную графически на рисунке 4.8.
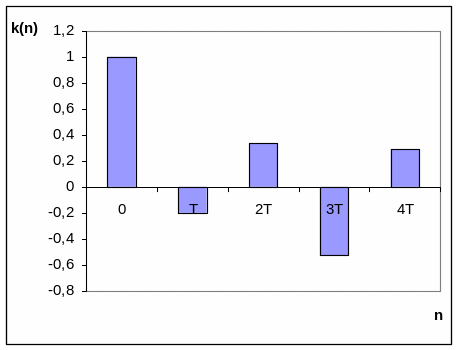
Рисунок 4.8 Импульсная Характеристика фильтра БИХ