2.1.5. Транспортная задача.

Внесем ясность в сущность транспортной задачи, несколько переформулировав стандартную постановку. Пусть некое предприятие решило оптимизировать свои систематические транспортные расходы по поставке груза в собственные каналы распределения. В структуру предприятия входят m поставщиков и n потребителей. Обозначим через: Mi ­­­- мощность поставщиков, Nj - спросы потребителей, cij - коэффициенты затрат на перевозку единицы груза для каждой пары "поставщик - потре­битель".

Найти объемы перевозок для каждой пары так, чтобы: мощности всех поставщиков были реализованы; спросы всех потребителей удовлетворены; суммарные затраты на перевозку были минимальны

Поставщики	Мощ- ность постав- щиков	Потребители и их спрос
		1	2	…	n
		N1	N2	…	Nn
1	M1	c11 x11	c12 x12		c1n x1n
2	M2	c21 x21	c22 x22		c2n x2n
…
m	Mm	cm1 xm1	cm2 xm2		cmn xmn

Решение. Искомый объем перевозки от i-го поставщика к j-му потребителю обозначим через хij и назовем поставкой клетки (i,j) Например, х12 — искомый объем перевозки от 1-го поставщика ко 2-му потребителю или поставка клетки (1,2) и т. д.

Заданные мощности поставщиков и спросы потребите­лей накладывают ограничения на значения неизвестных хij. Так, например, объем груза, забираемого от 1-го поставщика, должен быть равен мощности этого поставщика — M1 едини­цам, т.е. х11 + х12 + … + х1n = M1 (уравнение баланса по пер­вой строке). Таким образом, чтобы мощность каждого из по­ставщиков была реализована, необходимо составить уравнения баланса для каждой строки таблицы поставок, т. е.

Система ограничений выглядит

- уравнение баланса по строкам;

- уравнение баланса по столбцам.

для любых xij>=0. Линейная функция:

Математическая формулировка задачи в общей постановке будет следующей: на множестве неотрицательных (допустимых) решений системы ограничений найти такое решение Х= (х11, x12, …, xij, ..., хmn), при котором значение линейной функции минимально.

Особенности экономико-математической модели транс­портной задачи:

система ограничений есть система уравнений (т.е. транспорт­ная задача задана в канонической формe);

коэффициенты при переменных системы ограничений равны единице или нулю;

каждая переменная входит в систему ограничений два раза.

Если , то такая задача называется закрытой. Иначе – открытой.

Транспортной задаче в линейном программировании уделяется достаточно большой раздел и уже предполагается, что читатель ознакомлен методами решения подобных задач, поэтому, не прибегая к подробностям, напомним наименования методов решения:

Метод потенциалов;

Метод северо-западного угла;

Симплекс метод для решения транспортных задач и др.

Для всех методов первым этапом является определение начального распределения (начальных поставок). Для этого начального этапа в свою очередь имеется тоже ряд методов: метод северо-западного угла, наименьших стоимостей, аппроксимации Фогеля, двойного предпочтения и т.д.

Задачи сетевого планирования и управления рассматривают соот­ношения между сроками окончания крупного комплекса опера­ций (работ) и моментами начала всех операций комплекса. Эти задачи состоят в нахождении минимальных продолжительностей комплекса операций, оптимального соотношения величин стои­мости и сроков их выполнения.

Задачи массового обслуживания посвящены изучению и анализу систем обслуживания с очередями заявок или требований и со­стоят в определении показателей эффективности работы систем, их оптимальных характеристик, например, в определении числа каналов обслуживания, времени обслуживания и т.п.

Задачи управления запасами состоят в отыскании оптимальных значений уровня запасов (точки заказа) и размера заказа. Особен­ность таких задач заключается в том, что с увеличением уровня запасов, с одной стороны, увеличиваются затраты на их хранение, но с другой стороны, уменьшаются потери вследствие возможного дефицита запасаемого продукта.

Задачи распределения ресурсов возникают при определенном на­боре операций (работ), которые необходимо выполнять при огра­ниченных наличных ресурсах, и требуется найти оптимальное распределение ресурсов между операциями или состав операций

Задачи ремонта и замены оборудования актуальны в связи с из­носом и старением оборудования и необходимостью его замены с течением времени. Задачи сводятся к определению оптимальных сроков, числа профилактических ремонтов и проверок, а также моментов замены оборудования модернизированным.

Задачи составления расписания (календарного планирования) со­стоят в определении оптимальной очередности выполнения опе­раций (например, обработки деталей) на различных видах обо­рудования.

Задачи планировки и размещения состоят в определении оп­тимального числа и места размещения новых объектов с уче­том их взаимодействия с существующими объектами и между собой.

Задачи выбора маршрута, или сетевые задачи, чаще всего встречаются при исследовании разнообразных задач на транспор­те и в системе связи и состоят в определении наиболее эконо­мичных маршрутов.

2.2 Общая задача линейного программирования.

Дана система m линейных уравнений и неравенств с n переменными

и линейная функция

Необходимо найти такое решение системы X=(x1, x2,…, xk,…, xn), где xk 0 (k n), при котором линейная функция принимает оптимальное значение (max/min)

Система называется системой ограничений, а функция – линейной функцией, линейной формой, целевой функцией или функцией цели.

Краткая форма записи (Ф1)	Матричная форма записи (Ф2)	Векторная форма записи Ф(3)
при ограничениях:	F=CX →max(min) при ограничениях .	F=CX →max(min) при ограничениях где CX – скалярное произведение векторов ,

Оптимальным решением (оптимальным планом) задачи линейного программирования называется решение X=(x1, x2,…, xk,…, xn) системы ограничений и удовлетворяющее условию допустимости переменных, при котором линейная функция принимает оптимальное значение.

2.3 Методы решения задач линейного программирования

Если в ЗЛП ограничения заданы в виде неравенств с дву­мя переменными, она может быть решена графически.

Геометрический(графический) метод:

Множество допустимых решений (многогранник решений) задачи линейного программирования представляет собой выпуклый многогранник (или выпуклую многогранную область), а оптимальное решение задачи находит­ся, по крайней мере, в одной из угловых точек многогранника решений.

Симплексный метод:

Практическое осуществление пе­ребора всех угловых точек многогранника решений связано с огромными трудностями, так как для реальных задач число допус­тимых базисных решений хотя и конечно, но может быть чрезвы­чайно велико. Число перебираемых допустимых базисных решений можно сократить, если производить перебор с учетом изменений линейной функции, т.е. добиваясь того, чтобы каждое следующее решение было "лучше" (или, по крайней мере, "не хуже"), чем предыдущее, по значениям линейной функции. Такой перебор позволяет сократить число шагов при отыска­нии оптимума. Этот метод последовательного улучшения решения называется симплексным. Методологической основой симплексного (простого) метода являются рассмотренные выше теоремы, из которых следует: если ЗЛП имеет оптимальное решение, то оно соответствует хотя бы одной угловой точке многогранника решений и совпадает с одним из допустимых базисных решений систе­мы ограничений.

2.5 Двойственная задача ЛП.

Задаче ЛП соответствует другая задача, называемая двойственной или сопряженной по от­ношению к исходной. Теория двойственности полезна для проведения качественных исследований задач линейного программирования.

Пусть имеются две задачи линейного программирования обладающие следующими особенностями:

В одной задаче ищут максимум линейной функции, в другой — минимум;

Коэффициенты при переменных в целевой функции одной за­дачи являются свободными членами системы ограничений в другой;

Каждая из задач задана в стандартной форме, причем в задаче максимизации все неравенства вида "<=", а в задаче минимизации — все неравенства вида ">=";

Матрицы коэффициентов при переменных в системах ограни­чений обеих задач являются транспонированными друг к другу:

Для задачи I: Для задачи II:

Число неравенств в системе ограничений одной задачи совпа­дает с числом переменных в другой задаче;

Условия неотрицательности переменных имеются в обеих за­дачах,

то эти задачи линейного программирования, обладающие ука­занными свойствами, называются симметричными взаимно двойст­венными задачами. Будем называть их просто двойственными задачами.

Экономическое значение двойственности

Вспомним задачу об использовании ресурсов.

bi - запас ресурса Si;

aij — число единиц ресурса Si, потребляемого при производстве едини­цы продукции Pj;

сj - цена продукции Pj.

Допустим, что некоторая сторонняя организация решила закупить ресурсы S1, S2,...,Sm. Необходимо установить оп­тимальные цены на эти ресурсы y1, y2, ..., ут.

Очевидно, что покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z в количествах b1, b2, ..., bт по ценам соответственно y1, y2, ..., ут были минимальны, т.е

С другой стороны, предприятие, продающее ресурсы, заинте­ресовано в том, чтобы полученная выручка была не менее той суммы, которую предприятие может получить при переработке ресурсов в готовую продукцию. На изготовление единицы про­дукции Р1 расходуется

a11 единиц ресурса S1,

a21 единиц ресурса S2,

...

am1 единиц ресурса Sm,

по цене соответственно у1, y2, ..., yi, ..., ут. Поэтому для удовлетворения требований продавца предлагаемая цена за ресурсы, потребляемые при изго­товлении единицы продукции Р1, должны быть не менее цены продукта с1, т.е.

Аналогично можно составить ограничения в виде неравенств по каждому виду продукции.

Задача I (исходная)	Задача I (двойственная)
F= с1х1 + с2х2 +...+ сnхn →max при ограничениях: и условии … , Составить такой план выпуска продукции X = (х1 х2, ..., хm), при котором прибыль (выручка) от реализации продукции будет мак­симальной при условии, что по­требление ресурсов по каждому виду продукции не превзойдет имеющихся запасов.	Z= b1y1 + b2y2 +...+ bmym →min при ограничениях: и условии … , Найти такой набор цен (оценок) ресурсов Y =( y1, y2, ..., ут), при котором общие затраты на ресурсы будут минимальными при условии, что затраты на ресурсы при произ­водстве каждого вида продукции будут не менее прибыли (выручки) от реализации этой продукции

Цены ресурсов у1, у2, ..., ут называются учетными, неявными, теневыми. Смысл этих названий состоит в том, что это условные, "ненастоящие" цены. В отличие от внешних цен с1, с2, ..., сn на продукцию, известных, как правило, до начала производства, цены ресурсов у1, y2, ..., ут являются внутренними, ибо они задаются не извне, а определяют­ся непосредственно в результате решения задачи, поэтому их ча­ще называют оценками ресурсов.

Правило построения двойственной задачи:

Если в исходной задаче ищут мак­симум линейной функции, то все неравенства системы ог­раничений привести к виду " ", а если минимум — к виду " ". Для этого неравенства, в которых данное требование не выполняется, умножить на -1.

Составить расширенную матрицу системы А1, в которую включить матрицу коэффициентов при переменных А, стол­бец свободных членов системы ограничений и строку ко­эффициентов при переменных в линейной функции.

Найти матрицу , транспонированную к матрице А1.

Сформулировать двойственную задачу на основании полученной матрицы и условия неотрицательности переменных.

Мощным средством анализа данных Excel является надстройка Solver (Поиск решения). С ее помощью можно определить, при каких значениях указанных влияющих ячеек формула в целевой ячейке принимает нужное значение (минимальное, максимальное или равное какой-либо величине). Для процедуры поиска решения можно задать ограничения, причем не обязательно, чтобы при этом использовались те же влияющие ячейки. Для расчета заданного значения применяются различные математические методы поиска. Вы можете установить режим, в котором полученные значения переменных автоматически заносятся в таблицу. Кроме того, результаты работы программы могут быть оформлены в виде отчета. Программа Поиск решений (в оригинале Excel Solver) – дополнительная надстройка табличного процессора MS Excel, которая предназначена для решения определенных систем уравнений, линейных та нелинейных задач оптимизации, используется с 1991 года. Размер задачи, которую можно решить с помощью базовой версии этой программы, ограничивается такими предельными показателями:

• количество неизвестных (decision variable) – 200;

• количество формульных ограничений (explicit constraint) на неизвестные – 100;

• количество предельных условий (simple constraint) на неизвестные – 400.

Р азработчик программы Solver компания Frontline System уже давно специализируется на разработке мощных и удобных способов оптимизации, встроенных в среду популярных табличных процессоров разнообразных фирм-производителей (MS Excel Solver, Adobe Quattro Pro, Lotus 1-2-3). Высокая эффективность их применения объясняется интеграциею программы оптимизации и табличного бизнес-документа. Благодаря мировой популярности табличного процессора  MS Excel встроенная в его среду программа  Solver есть  наиболее распространенным инструментом для поиска оптимальных решений в сфере современного бизнеса. По умолчанию в Excel надстройка Поиск решения отключена. Чтобы активизировать ее в Excel 2007, щелкните значок Кнопка Microsoft Office , щелкните Параметры Excel, а затем выберите категорию Надстройки. В поле Управление выберите значение Надстройки Excel и нажмите кнопку Перейти. В поле Доступные надстройки установите флажок рядом с пунктом Поиск решения и нажмите кнопку ОК.

В Excel 2003 и ниже выберите команду Сервис/Надстройки, в появившемся диалоговом окне Надстройки установите флажок Поиск решения и щелкните на кнопке ОК. Если вслед за этим на экране появится диалоговое окно с предложением подтвердить ваши намерения, щелкните на кнопке Да. (Возможно, вам понадобится установочный компакт-диск Office).

По умолчанию, она отсутствует. Для активации следует в 2010 офисе сделать следующее: Файл – Параметры – Надстройки

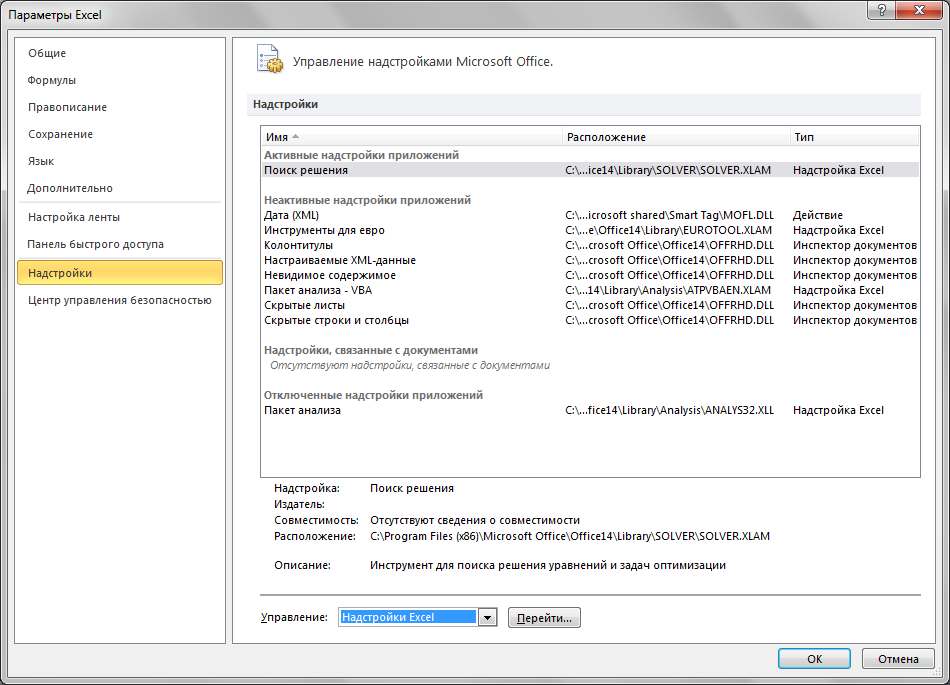
Нажать кнопку Перейти и поставить галочку у нужного пункта.

После этого во вкладке Данные появится блок Анализ.

Для 2003-го офиса следует выбрать Сервис – Надстройки.

Процедура поиска решения 1. Создайте таблицу с формулами, которые устанавливают связи между ячейками.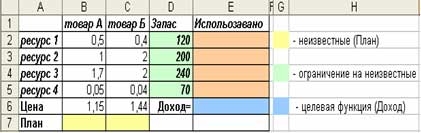

2. Выделите целевую ячейку, которая должна принять необходимое значение, и выберите команду: - В Excel 2007 Данные/Анализ/Поиск решения; - В Excel 2003 и ниже Tools > Solver (Сервис > Поиск решения). Поле Set Target Cell (Установить целевую ячейку) открывшегося диалогового окна надстройки Solver (Поиск решения) будет содержать адрес целевой ячейки. 3. Установите переключатели Equal To (Равной), задающие значение целевой ячейки, — Мах (максимальному значению), Min (минимальному значению) или Value of (значению). В последнем случае введите значение в поле справа. 4. Укажите в поле By Changing Cells (Изменяя ячейки), в каких ячейках программа должна изменять значения в поисках оптимального результата. 5. Создайте ограничения в списке Subject to the Constraints (Ограничения). Для этого щелкните на кнопке Add (Добавить) и в диалоговом окне Add Constraint (Добавление ограничения) определите ограничение.

6. Щелкните на кнопке на кнопке Options (Параметры), и в появившемся окне установите переключатель Неотрицательные значения (если переменные должны быть позитивными числами), Линейная модель (если задача, которую вы решаете, относится к линейным моделям)

7. Щелкнув на кнопке Solver (Выполнить), запустите процесс поиска решения.

8 . Когда появится диалоговое окно Solver Results (Результаты поиска решения), выберите переключатель Keep Solve Solution (Сохранить найденное решение) или Restore Original Values (Восстановить исходные значения). 9. Щелкните на кнопке ОК.

 

Параметры средства Поиск решения Максимальное время -  служит для ограничения времени, отпущенного на поиск решения задачи. В этом поле можно ввести время в секундах, не превышающее 32 767 (примерно девять часов); значение 100, используемое по умолчанию, вполне приемлемо для решения большинства простых задач.

Предельное число итераций - управляет временем решения задачи путем ограничения числа вычислительных циклов (итераций). Относительная погрешность - определяет точность вычислений. Чем меньше значение этого параметра, тем выше точность вычислений. Допустимое отклонение - предназначен для задания допуска на отклонение от оптимального решения, если множество значений влияющей ячейки ограничено множеством целых чисел. Чем больше значение допуска, тем меньше времени требуется на поиск решения. Сходимость - применяется только к нелинейным задачам. Когда относительное изменение значения в целевой ячейке за последние пять итераций становится меньше числа, указанного в поле Сходимость, поиск прекращается. Линейная модель - служит для ускорения поиска решения путем применения к задаче оптимизации линейной модели. Нелинейные модели предполагают использование нелинейных функций, фактора роста и экспоненциального сглаживания, что замедляет вычисления. Неотрицательные значения - позволяет установить нулевую нижнюю границу для тех влияющих ячеек, для которых не было задано соответствующее ограничение в диалоговом окне Добавить ограничение. Автоматическое масштабирование - используется, когда числа в изменяемых ячейках и в целевой ячейке существенно различаются. Показывать результаты итераций - приостанавливает поиск решения для просмотра результатов отдельных итераций. Загрузить модель - после щелчка на этой кнопке отрывается одноименное диалоговое окно, в котором можно ввести ссылку на диапазон ячеек, содержащих модель оптимизации. Сохранить модель - служит для отображения на экране одноименного диалогового окна, в котором можно ввести ссылку на диапазон ячеек, предназначенный для хранения модели оптимизации. Оценка линейная - выберите этот переключатель для работы с линейной моделью. Оценка квадратичная - выберите этот переключатель для работы с нелинейной моделью. Разности прямые - используется в большинстве задач, где скорость изменения ограничений относительно невысока. Увеличивает скорость работы средства Поиск решения. Разности центральные - используется для функций, имеющих разрывную производную. Данный способ требует больше вычислений, однако его применение может быть оправданным, если выдано сообщение о том, что получить более точное решение не удается. Метод поиска Ньютона - требует больше памяти, но выполняет меньше итераций, чем в методе сопряженных градиентов. Метод поиска сопряженных градиентов - реализует метод сопряженных градиентов, для которого требуется меньше памяти, но выполняется больше итераций, чем в методе Ньютона. Данный метод следует использовать, если задача достаточно большая и необходимо экономить память или если итерации дают слишком малое отличие в последовательных приближениях.