Определение

С древних времен люди в своих творениях предпочитают правильные геометрические формы – квадрат, круг, пирамиду и т.д. Симметричные фигуры предпочтительнее, чем несимметричные.

При создании произведений искусства пользовались различными пропорциями. Но из многих пропорций, которыми издавна пользовался человек, существует одна, единственная и неповторимая, обладающая уникальными свойствами. Она отвечает такому делению целого на две части, при котором отношение большей части к меньшей равно отношению целого к большей части. Эту пропорцию называли по разному: «золотой», «божественной», «золотым сечением», «золотым числом».

Если симметричность в архитектуре придает зданиям величественность, совершенность, но она «холодная», «неподвижная», то золотая пропорция придает зданиям грацию, неповторимую индивидуальность, особую гармонию – «подвижную» и «одухотворенную».

Если определении золотой пропорции перевести на язык формул, то получим:

, т.к. x > 0, то

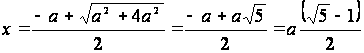
Принято обозначать: 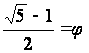 . Число   носит название коэффициента золотого сечения;  =0,61803389… или  =0,618. Заметим, что:

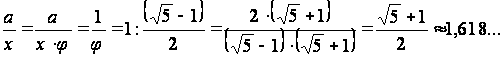
Принято обозначать:

.

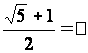Золотое сечение - это такое деление целого на две неравные части, при котором большая часть так относится к целому, как меньшая часть - к большей. В геометрии Золотое сечение называется также делением отрезка в крайнем и среднем отношении. 

Части «Золотого сечения» составляют приблизительно 62 % и 38 % всего отрезка.

Золотое сечение – понятие математическое, но оно является критерием гармонии и красоты в  архитектуре и искусстве.

Числа Фибоначчи

  Был такой математик Леонардо Пизанский, известный как Фибоначчи. Выдающейся заслугой Леонардо Фибоначчи является ряд чисел Фибоначчи. Этот ряд чисел, образующих последовательность 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ...   каждое следующее число получается в результате сложения двух предыдущих. У этого ряда есть замечательные особенности! Спустя четыре столетия после открытия Фибоначчи ряда чисел И.Кеплер установил, что отношение рядом стоящих чисел

в пределе стремится к золотой пропорции. Отношение каждого числа к последующему более и более стремится к 0.618 при увеличении порядкового номера. Отношение же каждого числа к предыдущему стремится к 1.618 (обратному к 0.618). Число 0.618 называют  φ.    Число  φ -  иррациональное, оно равно  φ  =  0,618033989 …. На практике  пользуются числом φ, взятым с точностью до тысячных 0,618, или до сотых 0,62, или до десятых 0,6.  

Если делить всё большие и большие числа Фибоначчи, то наиболее близко можно подойти к золотому сечению.

Золотое сечение в архитектуре.

Сотворение поистине гармоничного пространства невозможно без ясного осознания принципов создания и обустройства своего жилища. Наши предки на протяжении тысяч лет накапливали опыт в строительстве как отдельных домов, так и целых поселений

Великолепные памятники архитектуры оставили нам зодчие Древней Греции.

И среди них первое место по праву принадлежит Парфенону. Высота

Парфенона 61,8 футов, высота трех ступеней основания и колонны – 38,2 футов,

высота перекрытия и фронтона – 23,6 футов. Указанные размеры образуют ряд

золотой пропорции: 100 : 61,8 = 61,8 : 38,2 = 38,2 :23,6 »1,6 = Ф. указанные

отношения приблизительно равны числу 1,6, т.е. образуют «золотую пропорцию».

Многие исследователи, стремившиеся раскрыть секрет гармонии Парфенона,

искали и находили в соотношениях его частей золотую пропорцию. На плане пола

Парфенона также можно заметить «золотые прямоугольники».

О египетских пирамидах с восхищением писал греческий историк Геродот.

Согласно многим описаниям, эти гигантские монолиты имели совсем иной вид,

чем в наше время. Они сияли на солнце белой глазурью отполированных известняковых плит на фоне многоколонных прилегающих храмов.

Среди грандиозных пирамид Египта особое место занимает великая пирамида фараона Хеопса. Она самая крупная и наиболее хорошо изученная. Чего только не

находили в ее пропорциях! Число «пи» и золотое сечение, число дней в году, расстояние до Солнца, диаметр Земли.

Архитектура русских православных храмов и соборов свидетельствуют о том, что с древнейших времен архитекторы хорошо знали математическую пропорцию

и вписывали свои сооружения в правило Золотого прямоугольника: Собор на Нерли, Собор святой Елизаветы в Санкт-Петербурге, Храм Христа Спасителя в Москве.

В древнерусской архитектуре количество глав, связанных с конструкцией храмов,  следуют численному ряду Фибоначчи: 1, 3, 5, 8, 13, 21.  Храм Василия Блаженного имеет 1+8 = 9 глав, храм Святой Софии в Киеве - 13 глав.

• Знаменитый русский архитектор М.Ф.Казаков широко использовал в своем творчестве золотое сечение. Его талант был многогранным, но в большей степени он проявился в многочисленных проектах жилых домов и усадеб. Например, золотое сечение можно встретить в архитектуре здания бывшего сената в Кремле, Дворца в Петровском Алабине и Голицынской больницы в Москве, которая в настоящее время называется Первой Клинической больницей имени Н.И.Пирогова. Еще один архитектурный шедевр Москвы - дом Пашкова - является одним из наиболее совершенных произведений архитектора В.Баженова. Наружный вид дома сохранился почти без изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 году. Многие высказывания зодчего заслуживают внимания. О своем любимом искусстве Баженов говорил: "Архитектура - главнейшие имеет три предмета: красоту, спокойствие и прочность здания. К достижению сего служит руководством знание пропорции, перспективы, механики или вообще физики, а всем им общим вождем является рассудок". Шедеврами архитектуры являются многие русские храмы, которые строились на протяжении нескольких столетий. В плане стены храмов или опорные колонны обычно вписываются в квадрат или прямоугольник со сторонами 1:2

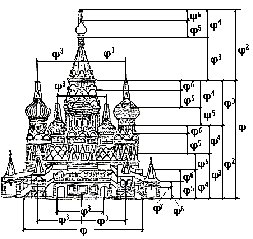
Трудно найти человека, который бы не знал и не видел собора Василия Блаженного на Красной площади. Храм этот особенный; он отличается удивительным разнообразием форм и деталей, красочных покрытий; ему нет равных в нашей стране. Архитектурное убранство всего собора продиктовано определенной логикой и последовательностью развития форм. Исследуя его, пришли к выводу о преобладании в нем ряда золотого сечения. Если принять высоту собора за единицу, то основные пропорции, определяющие членение целого на части, образуют ряд золотого сечения: 1 : j : j 2 : j 3 : j 4 : j 5 : j 6 : j 7, где j =0,618 

 Главное здание МГУ на Воробьёвых горах  - это центральное здание университетского комплекса МГУ на Воробьёвых горах. Выстроено с 1949 – 1953 г.  

 1) – основные размеры здания (высота 182 метра длина 292 метра),:

                                     18200

                                         29200  ≈ 0,623;

2) –    общие    размеры     крайних    боковых     башен   с     часами   основного    здания:    

                                         10000

                                         26200  ≈ 0,381.

Гостиница  «Украина»  Вторая по высоте «Сталинская высотка» построена в 1953—1957 годах.

1) – основные размеры здания (высота 133 метра длина 214 метра),:  

                 13300

                 21400  ≈ 0,621;   

2) – общие размеры крайних боковых   башен с вазами стоящие на беседках:   

                  7600

                19800  ≈ 0,383.

    Полученные  отношения  приблизительно равны, Золотой пропорции, т.е. приблизительно составляет 62% и 38% что, являются частями Золотого сечения

Исследование 1.Нахождение коэффициента золотой пропорции по фотографиям.

2.Нахождения коэффициента золотой

пропорции в здании нашей школы.

Проанализировать план нашей школы ,

произвести измерения основных размеров зданий, клумб, спортплощадок.