4 Синтез цифровых фильтров и фильтрация сигналов в пакете simulink

4.1 Мета роботи: изучить методы синтеза и анализа цифровых фильтров, а также основы применения цифровой фильтрации сигналов.

4.2 Методичні вказівки з організації самостійної роботи студентів:

1. Освоить средство синтеза и анализа цифровых фильтров FDAtool библиотеки DSP blockset пакета Simulink.

2. Изучить характеристики различных типов цифровых фильтров и научится их синтезировать с помощью средства FDAtool.

3. Освоить аналитические подходы к исследованию характеристик цифровых фильтров (расчет импульсной характеристики, оценка устойчивости).

4. Исследовать временные и спектральные характеристики заданных сигналов до, и после фильтрации.

Пример выполнения задания.

Набрав в командном окне пакета MATLAB команду «fdatool», загружаем приложение FDAtool – Filter Design & Analysis Tool – средство проектирования и анализа фильтров.

В окне настроек Filter Design & Analysis Tool задаём необходимые по условию параметры:

• тип фильтра выбираем в группе Design Method в раскрывающихся списках FIR (КИХ-фильтр – фильтр с конечной импульсной характеристикой) или IIR (БИХ-фильтр - фильтр с бесконечной импульсной характеристикой). Выбираем IIR и фильтр Chebyshev Type II (фильтр Чебышева 2);

• тип характеристики фильтра задаём в группе Response Type с помощью переключателей: Lowpass (ФНЧ), Highpass (ФВЧ), Bandpass (ПФ) или Bandstop (РФ). Выбираем Bandpass – полоснопропускающий фильтр;

• устанавливаем частоту дискретизации, задаваемую в группе Frequency Specifications. Предварительно в раскрывающемся списке Units (единицы измерения) указываем единицы Hz (Гц), после чего задаём частоту в поле ввода Fs = 1000 и частоты среза в полях Fstop1 = 250, Fstop2 = 350;

• порядок фильтра выбираем в группе Filter Order – выбираем Specify Order (конкретный произвольный порядок) и устанавливаем значение 4;

При нажатии кнопки Design Filter производится синтез цифрового фильтра по заданным параметрам.

На рисунке 3.1 представлено окно настроек приложения Filter Design & Analysis Tool после настройки всех необходимых параметров и синтеза ЦФ.

В группе Filter Information (текущая информация о фильтре) получаем данные о созданном фильтре – его структура, порядок, устойчивость и др.

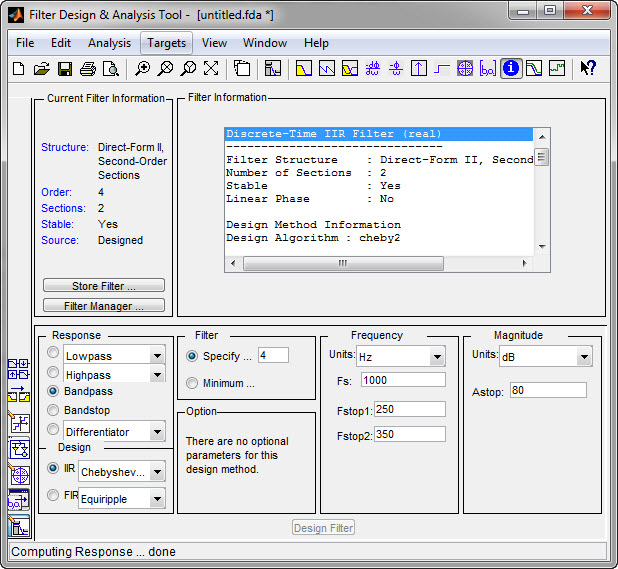
Рисунок 4.1 - Окно настроек Filter Design & Analysis Tool после синтеза ЦФ

При нажатии Magnitude Response мы получаем график АЧХ фильтра, Phase Response показывает ФЧХ фильтра.

На Рисунках 4.2 и 4.3 представлены графики АЧХ и ФЧХ фильтра Чебышева второго типа для различных порядков фильтра – 4, 6 и 10 соответственно.

Как видно из графиков АЧХ, фильтр Чебышева второго типа с увеличением порядка стремится к идеальному фильтру, при этом уменьшается ширина переходной полосы, постепенно (при приближении к частоте среза) увеличивается частота пульсаций в полосе задерживания при их неизменной амплитуде.

На ФЧХ фильтра Чебышева второго типа до частоты среза можно выделить линейный участок, на частотах выше частоты среза на ФЧХ появляются пилообразные пульсации, обозначающие смену фазы на π. При увеличении порядка фильтра увеличивается частота этих пульсаций, участок линейности ФЧХ с увеличением порядка уменьшается.

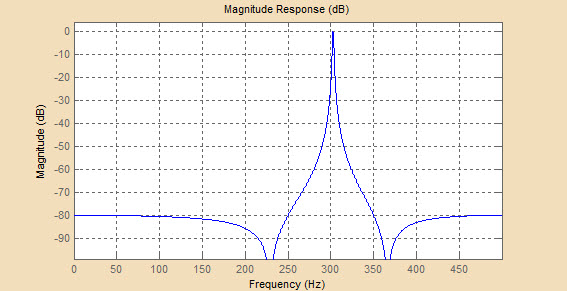
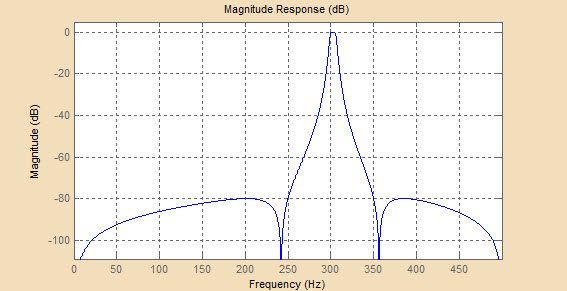
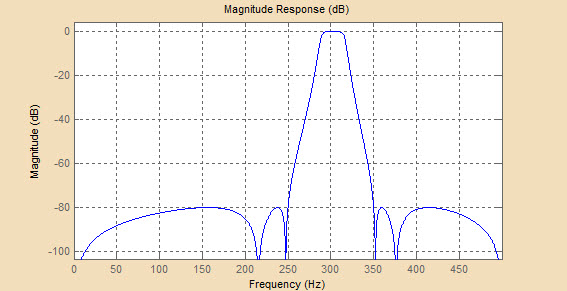
Рисунок 4.2 - Графики АЧХ для порядков фильтра 4, 6 и 10 соответственно

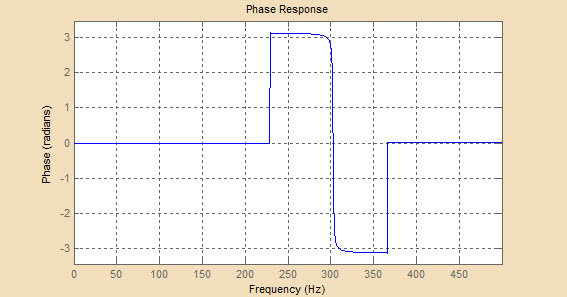
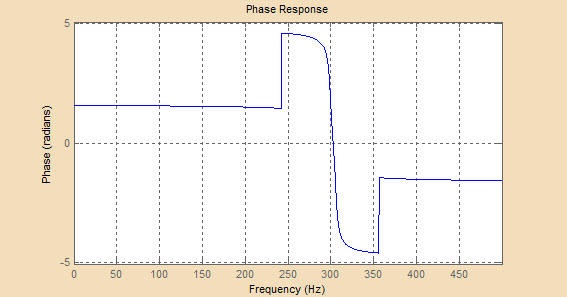
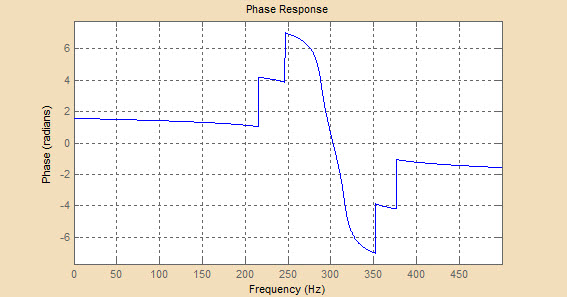
Рисунок 4.3 - Графики ФЧХ для порядков фильтра 4, 6 и 10 соответственно

Выбрав в группе настроек Analysis параметр Filter Coefficients, получаем информацию о коэффициентах фильтра, с помощью которой можно реализовать спроектированный фильтр. Далее File → Export…→ выбираем, куда и в каком формате экспортировать данные о коэффициентах фильтра. Экспортируя в Coefficient File (ASCII) как Decimal, получаем:

% Generated by MATLAB(R) 7.13 and the Signal Processing Toolbox 6.16.

% Coefficient Format: Decimal

% Discrete-Time IIR Filter (real)

% -------------------------------

% Filter Structure : Direct-Form II, Second-Order Sections

% Number of Sections : 2

% Stable : Yes

% Linear Phase : No

SOS matrix:

1 1.334394011671562 1 1 0.65385663890514478 0.99353025042178411

1 -0.26129531435914283 1 1 0.64159953067393216 0.99351583612192418

Scale Values:

0.010969508090157403

0.010969508090157403

Преобразование Edit → Convert to Single Section даёт значения коэффициентов:

Numerator:

0.00012033010774002873

0.00012912608186328782

0.00019870460818529272

0.0001291260818632879

0.00012033010774002875

Denominator:

1

1.2954561695790785

2.4065601991932866

1.2870654676866899

0.98708803746022578

Numerator – это значения коэффициентов числителя (b₀, b₁, …, b₅), а Denominator – значения коэффициентов знаменателя (a₀, a₁, …, a₅) из передаточной функции фильтра, общий вид формулы которой

H(z) = ,

где n – количество коэффициентов b, m – количество коэффициентов a. Для нашего случая m=n=5 и по найденным коэффициентам можно привести формулу алгоритма реализации конкретно данного фильтра.

Импульсную и переходную характеристики фильтра будем строить с помощью опций Impulse Response и Step Response.

Импульсная характеристика фильтра – реакция на 1 скачок - представлена на Рисунке 4.4. На Рисунке 4.5 представлен график переходной характеристики фильтра – реакции на единичное воздействие.

Как видно из графиков, импульсная и переходная характеристика фильтра БИХ имеет бесконечную длину во временной области. Обе характеристики стремятся к нулю, благодаря чему спроектированный фильтр является устойчивым.

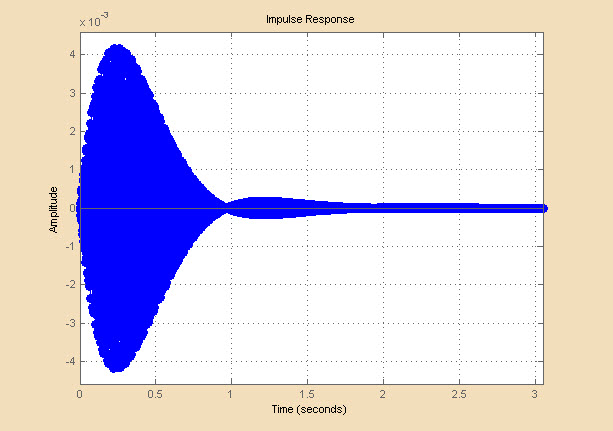
Рисунок 3.4. График импульсной характеристики фильтра

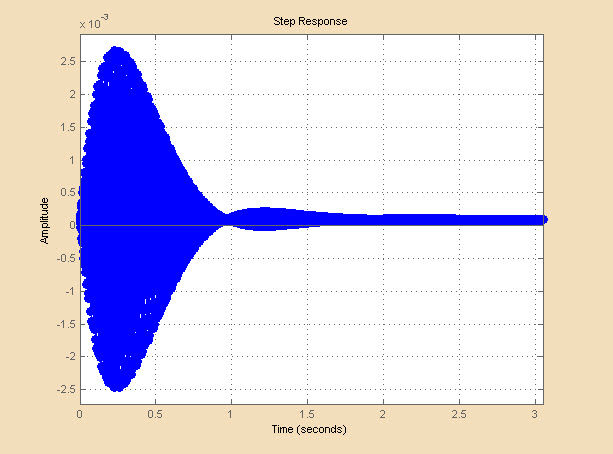
Рисунок 4.4 - График переходной характеристики фильтра

Включаем исследованный фильтр в модель второго задания и проводим моделирование (Рисунок 3.5)

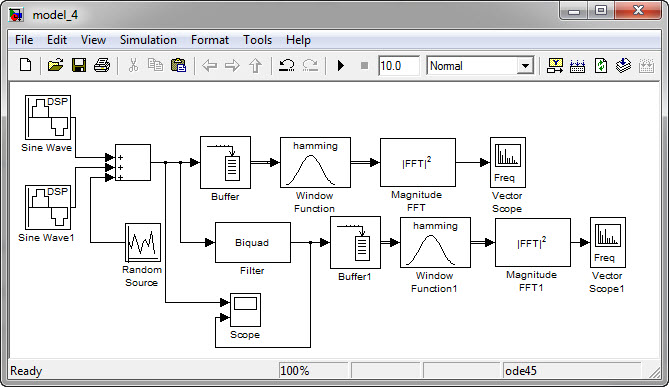
Рисунок 4.5 - Модель с заданным фильтром

Графики временных реализаций входного и выходного сигналов фильтра представлены на Рисунке 4.6.

Как видно из графиков, за границей полосы пропускания фильтр значительно ослабляет нежелательные колебания, присутствующие на соседних частотах. Но в то же время такая резкая крутизна подавления шумов может влиять на полезный сигнал и искажать его.

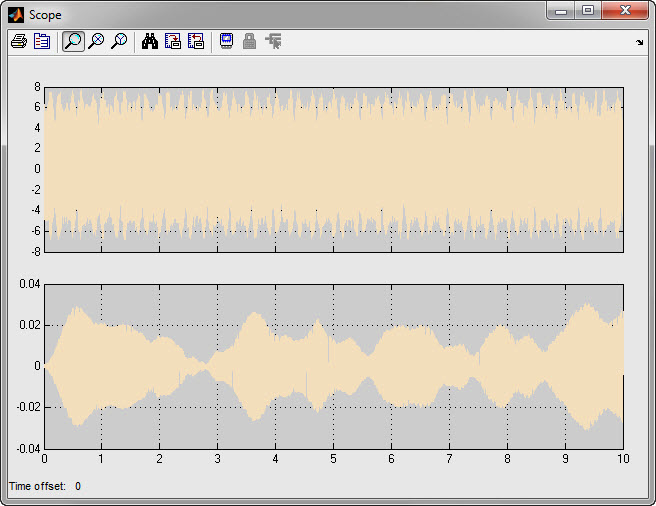
Рисунок 4.6 - Графики временных реализаций входного и выходного сигналов фильтра

Графики спектров входного и выходного сигналов фильтра получаем с помощью блоков Vector Scope и Vector Scope 1, они представлены на Рисунке 4.7.

Как видно на спектрах мощности сигнала до фильтрации и после, фильтр значительно подавляет шумы.

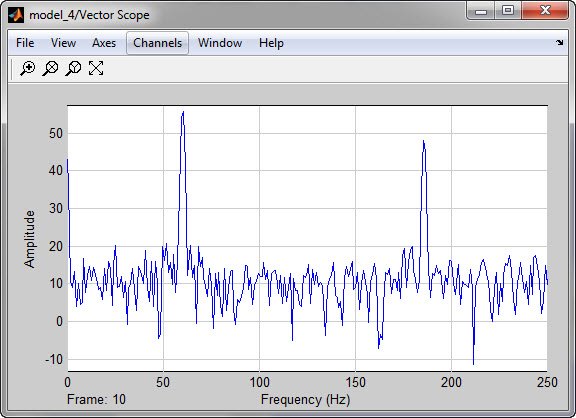
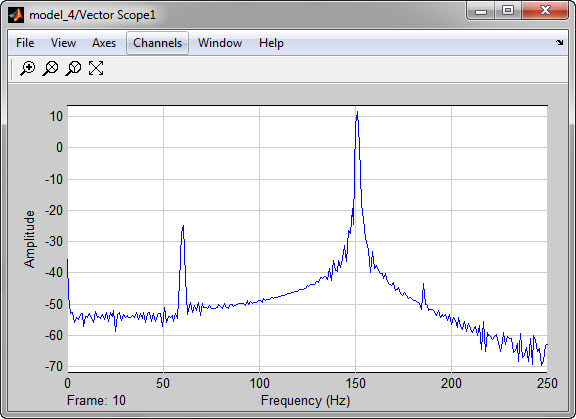
Рисунок 4.7- Спектры мощности сигнала до фильтрации и после

4.3 Опис лабораторної установки

Лабораторна робота буде виконуватися в програмі "Simulink MATLAB".

4.4 Порядок виконання роботи

4.4.1 Загрузить приложение FDAtool пакета MATLAB и ознакомиться с его возможностями и настройками.

4.4.2 Исследовать зависимости формы АЧХ и ФЧХ фильтра от порядка (использовать порядки - 4, 6, 10). Тип фильтра взять в соответствии с таблицей вариантов. Частота дискретизации равна 1000 Гц.

4.4.3 Привести формулу алгоритма реализации данного фильтра. Для этого использовать информацию о коэффициентах фильтра (реализуется с помощью FDAtool).

4.4.4 Построить импульсную и переходную характеристики, а также график групповой задержки заданного фильтра (реализуется с помощью FDAtool). Проанализировать данные характеристики.

4.4.5 Включить исследованный фильтр в модель второго задания. Провести моделирование.

4.4.6 Сравнить графики временных реализаций входного и выходного сигналов фильтра.

4.4.7 Получить и сравнить графики спектров входного и выходного сигналов фильтра. Для получения спектров использовать модели второго задания.

Таблица 4.1 – Варианты к заданию

№ варианта	Характеристики фильтра
	Характер фильтра	Тип фильтра	Порядок фильтра	Частота среза, Гц
1	ПФ	Чебышева	10	Fs/3, Fs/4
2	ФНЧ	Баттерворта
3	ФНЧ	Баттерворта
4	ФНЧ	Баттерворта
5	ПФ	Чебышева	6
6	ПФ	Чебышева	4
7	ФНЧ	Баттерворта
8	ФНЧ	Баттерворта
9	ФНЧ	Баттерворта
10	ПФ	Чебышева
11	ПФ	Чебышева
12	ПФ	Чебышева

4.5 Зміст звіту:

- модель фильтра согласно варианта задания;

- результаты расчёта параметров фильтра в соответствии с пунктами 4.4.2 -4.4.7.

4.6 Контрольні запитання та завдання

1. Какой вид имеют логарифмические характеристики фильтров низких частот?

2. Какой вид имеют логарифмические характеристики фильтров высоких частот?

3. Укажите на графиках точку, определяющую граничную частоту пропускания, и обоснуйте методику ее определения.

4. Укажите на графиках точку, определяющую граничную частоту задерживания, и обоснуйте методику ее определения.

5. Во сколько раз амплитуда выходного сигнала будет меньше амплитуды входного сигнала, если величина подавления составляет 6 дБ?

6. Во сколько раз амплитуда выходного сигнала будет меньше амплитуды входного сигнала, если величина подавления составляет 2 дБ?

7. Укажите расположение корней характеристического уравнения фильтра Баттерворта для n=1,2,3,4,5 (n – степень характеристического уравнения).

8. В какую сторону и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если интервал между граничной частотой пропускания и задерживания будет уменьшаться?

9. В какую сторону и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если интервал между граничной частотой пропускания и задерживания будет увеличиваться?

10. В какую сторону и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если максимально допустимое подавление в полосе частот пропускания будет уменьшаться?

11. В какую сторону и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если максимально допустимое подавление в полосе частот пропускания будет увеличиваться?

12. В какую сторону и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если максимально допустимое подавление в полосе частот подавления будет уменьшаться?

13. В какую сторону и почему будет изменяться степень характеристического уравнения фильтра Баттерворта, если максимально допустимое подавление в полосе частот подавления будет увеличиваться?

14. Какие исходные данные следует знать, чтобы определить порядок и частоту среза фильтра Баттерворта в абсолютных единицах?

15. Какие исходные данные следует знать, чтобы получить передаточную функцию фильтра Баттерворта с заданной частотой среза?

16. Как определяется, и какой график имеет характеристика затухания для фильтра Баттерворта?