2 Генерация сигналов в пакете simulink и оценка их энергетических характеристик

2.1 Мета роботи: Освоить основы моделирования сигналов систем связи в пакете Simulink и изучить способы математического описания сигналов.

2.2 Методичні вказівки з організації самостійної роботи студентів.

1. Освоить основы работы в пакете Simulink и ознакомиться с составами базовой библиотеки и библиотеки DSP blockset.

2. Научиться создавать, настраивать и исследовать модели сигналов в пакете Simulink.

3. Освоить создание математических моделей сигналов.

Пример выполнения задания.

Запустив программу MATLAB и нажав кнопку на панели инструментов командного окна MATLAB, запустить программу Simulink. Далее, нажав значок на панели инструментов обозревателя разделов библиотек, открыть рабочую область (новое окно модели) для создания новой модели. Используя наборы блок-схем, с помощью мыши перенести нужные компоненты на рабочий стол пакета Simulink и соединить линиями входы и выходы блоков.

Пусть задана математическая модель полигармонического сигнала:

,

тогда схема в терминах пакета Simulink будет иметь вид как показано Рисунке 2.1.

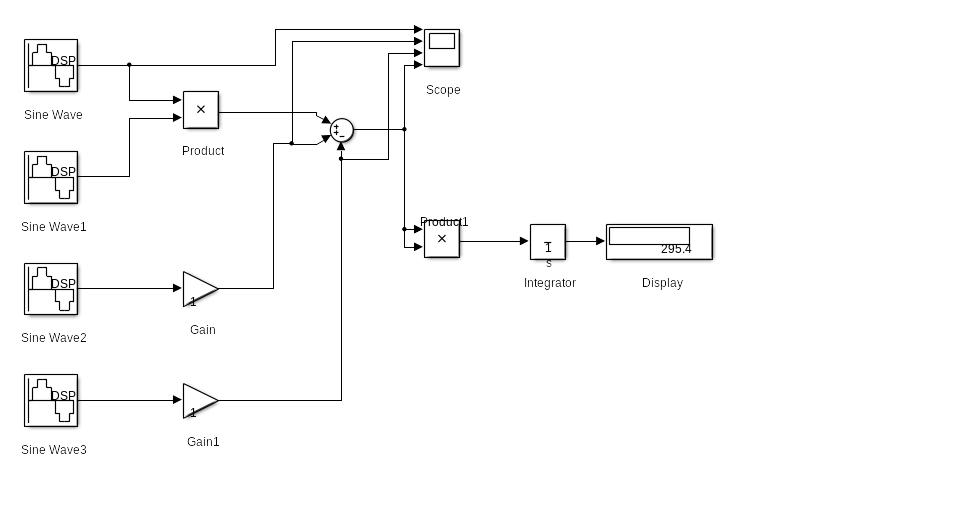
Рисунок 2.1 - Модель для исследования полигармонического сигнала

Модель создана из таких блоков:

1. Блок Sine Wave - Формирует синусоидальный сигнал с заданной частотой, амплитудой, фазой и смещением. В настройках блоков Sine Wave и Sine Wave1, исходя из математического уравнения сигнала, задаём амплитуду равной 1, частоту равной 2*pi*200. В блоках Sine Wave2 и Sine Wave3 амплитуды равны 6 и 4 соответственно, частоты - 2*pi*30 и 2*pi*20 соответственно.

2. Блок Product выполняет вычисление произведения текущих значений сигналов. Таким образом, мы реализуем «cos²».

3. Блок Gain выполняет умножение входного сигнала на постоянный коэффициент.

4. Блок Sum выполняет вычисление суммы текущих значений сигналов. В настройках блока задаём его форму – окружность – и список знаков – «|++-».

5. Результат суммирования выводится на блок Scope, который представляет собой осциллограф. Данный блок строит графики исследуемых сигналов в функции времени и позволяет наблюдать за изменениями сигналов в процессе моделирования.

Для верного симулирования процесса необходимо правильно задать параметр Sample time - шаг модельного времени, который используется для согласования работы источника и других компонентов модели во времени.

По условию задания ∆t = 70 мс = 0,07 с. Согласно теореме Котельникова, если аналоговый сигнал x(t) имеет ограниченный по ширине спектр, то он может быть восстановлен однозначно и без потерь по своим дискретным отсчётам, взятым с частотой строго большей удвоенной верхней частоты f_c:

f > 2f_c .

Таким образом,

1 / 0,07 ≥ 2∙f_max

2∙f_max ≤ 14,29

f_max ≤ 7

Sample time = 1/7

Значение параметра Sample time, равное 1/7, задаём в блоках Sine Wave, Product, Gain, Sum и Scope.

Отображение с помощью блока Scope сигнала, заданного по условию, математическая модель которого построена в пакете инструментов Simulink, представлено на Рисунке 2.2.

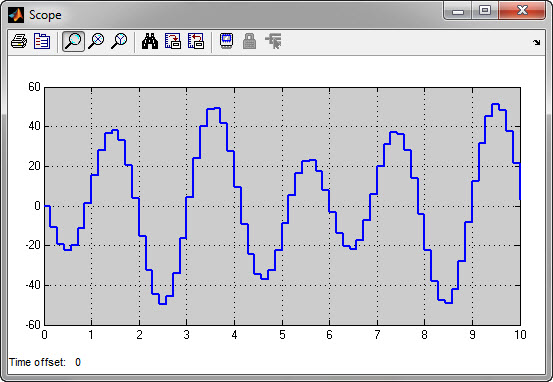
Рисунок 2.2 - График заданного по условию сигнала на осциллографе Scope

Для оценки энергетических параметров полигармонического сигнала строим модель сигнала по данным таблицы 2.2.

В новом окне создания модели помещаем блок Signal Builder, который позволяет задать сигнал произвольной формы, проектируемый самим пользователем.

В соответствии с исходными данными (таблица 2.2), строим два сигнала необходимой формы, задавая координаты точек.

1) Два клика на блок Signal Builder→Axes→Change Time Range→ для большей наглядности будущего графика максимально отображаемое время на графике (Max time) задаём равным 0,1 с, минимальное (Min time) = -0,001с.

2) Создаем график сигнала, аналогичный сигналу «1» таблицы исходных данных: Signal→New→Custom и в скобках «[ ]» через пробел перечисляем координаты точек: Time values [0 0,07 0,07], Y values [0 3 0]. Аналогично проектируем второй сигнал, равный сигналу «4» таблицы 2.2: Time values [0 0 0,07 0,07], Y values [0 3 3 0].

Графики созданных сигналов представлены на Рисунке 2.3.

Значение параметра Sample time, равное 1/7, задаём в блоках Signal builder, Sum, Product и Scope.

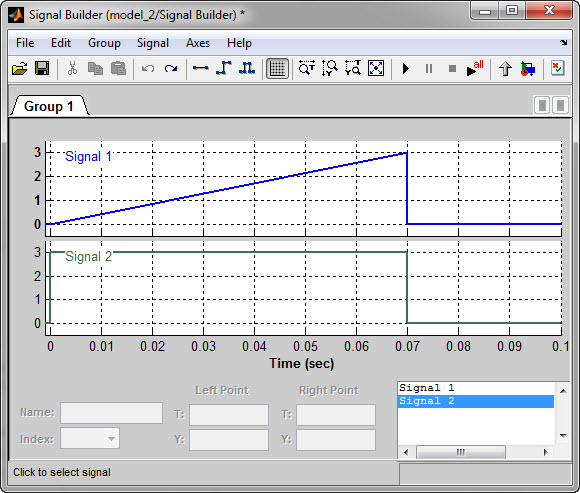
Рисунок 2.3 - Графики заданных сигналов в окне настроек блока Signal Builder

Далее суммируем сигналы с помощью блока Sum и результат отправляем на осциллограф Scope (Рисунок 2.4). В настройках блока Scope параметр «Time range» задаём также равным 0,1 с.

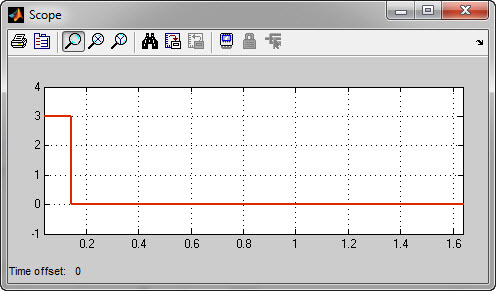
Рисунок 2.4 - График суммы сигналов

Для оценки энергии суммарного сигнала необходимо возвести сумму данных сигналов в квадрат с помощью блока Product и провести интегрирование результата с помощью блока Integrator, выход которого направляем на блок Display (Рисунок 2.5).

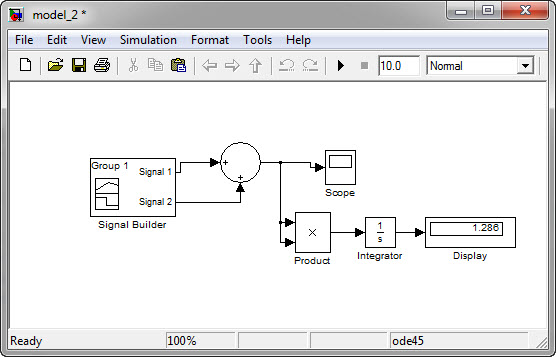
Рисунок 2.5 - Вычисление энергии сигнала

Блок Display показывает энергию сигналов первой группы = 1,268. Так как исследуемый сигнал – это сигнал напряжения, размерность его энергии равна [В²∙с].

Для того, чтобы вычислить энергию сигнала, заданного математическим уравнением (таблица 2.1), аналогично блок сумматора соединяем с блоком умножения, а затем – с блоком интегратора и блоком Display. В результате симуляции процесса получаем значение энергии, равное 8289 (В²∙с) (Рисунок 2.6).

Разделив энергию E на длительность временного интервала ∆t, получим среднюю мощность P_c.

Для сигнала, заданного математическим уравнением:

Р_с = Е / ∆t = 8289 / 0,07=118414,2857 (В²)

Для суммы сигналов, заданных в таблице 1.2:

Р_с = Е / ∆t = 1,268 / 0,07 = 18,11428517 (В²)

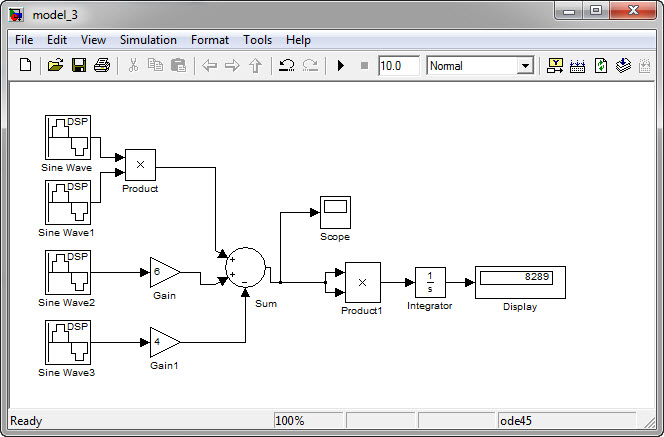
Рисунок 2.6 - Вычисление энергии сигнала, созданного по математической модели

2.3 Опис лабораторної установки

Лабораторна робота буде виконуватися в програмі "Simulink MATLAB".

2.4 Порядок виконання роботи

Загрузить пакет Simulink и ознакомиться с составом, назначением и настройками блоков базовой библиотеки и библиотеки DSP Blockset.

1. Используя блоки базовой библиотеки и библиотеки DSP Blockset, создайте модель сигнала согласно варианта задания (табл. 2.1).

2. Оцените на модели энергетические параметры сигнала (энергию, среднюю мощность).

Таблиця 2.1 – Варианты к заданию

№ варианта
	Типы сигналов		Т, мс	А, В	Математическая модель сигнала
1	1.1	1.3	70	5
2	1.2	1.4	70	4
3	1.3	1.4	70	3
4	1.1	1.2	50	10
5	1.2	1.3	50	8
6	1.5	1.6	50	12

Таблиця 2.2 – Графики моделируемых импульсных сигналов

Сигнал 1.1	Сигнал 1.2
Сигнал 1.3	Сигнал 1.4
Сигнал 1.5	Сигнал 1.6

2.5 Зміст звіту:

- модель сигнала согласно варианта задания;

- результаты расчёта энергетических параметров сигнала (энергия, средняя мощность).

2.6 Контрольні запитання та завдання

1. Определение мощности, энергии, среднее и пиковое значение мощности.

2. Как связаны между собой энергия и норма сигналов.

3. Как определяется энергия суммы двух произвольных сигналов u(t) и v(t).

4. Что называют скалярным произведением сигналов.

5. Поясните смысл неравенства Коши-Буняковского.

6. При рассмотрении каких сигналов используют гильбертово пространство и пространство Евклида.

7. Как выглядит скалярное произведение двух сигналов в пространстве Евклида.

8. Поясните смысл спектральной плотности энергии сигнала и энергетического спектра.