Занятие 4.1 Тригонометрические функции числового аргумента (определение, значения, знаки, чётность, нечётность, периодичность, ограниченность, основные тождества). Формулы приведения.

Любой угол измеряется либо в градусной мере измерения (единица измерения – градус) либо в радианной (единица измерения – радиан). Один дуговой градус – это часть окружности. Один угловой градус – это центральный угол, опирающийся на дуговой градус. Радианная мера угла – это отношение длины дуги к радиусу этой дуги. Радиан – это центральный угол, опирающийся на дугу, равную длине радиуса этой дуги. Окружность содержит радиан.

– радианная мера угла

радиан

1 рад

Для перехода от градусной меры измерения угла к радианной и наоборот можно пользоваться формулами: ;

Например:

1 ) Дано: 2) Дано:

Найти: Найти:

В прямоугольном треугольнике Для произвольного угла

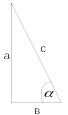
Основные тригонометрические тождества

Из определения:

любые значения

функции ограниченные

всегда растет (+)

всегда убывает (+)

Золотые углы

sin	0				1	0	–1	0
cos	1				0	–1	0	1
tg	0		1		–	0	–	0
ctg	–		1		0	–	0	–

Решить: 1) (совместно устно)

Самостоятельно: 2)

Решение:

1) ;

2)

Знаки функций по четвертям
	I	II	III	IV
	+	+	–	–
	+	–	–	+
	+	–	+	–
	+	–	+	–

Углы и

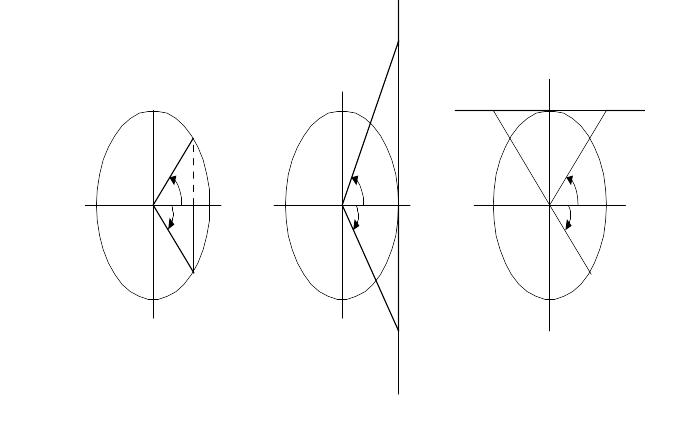
(нечётная)

(нечётная)

(нечётная)

Периодичность:

– период

– период

– период

Ф ормулы приведения:

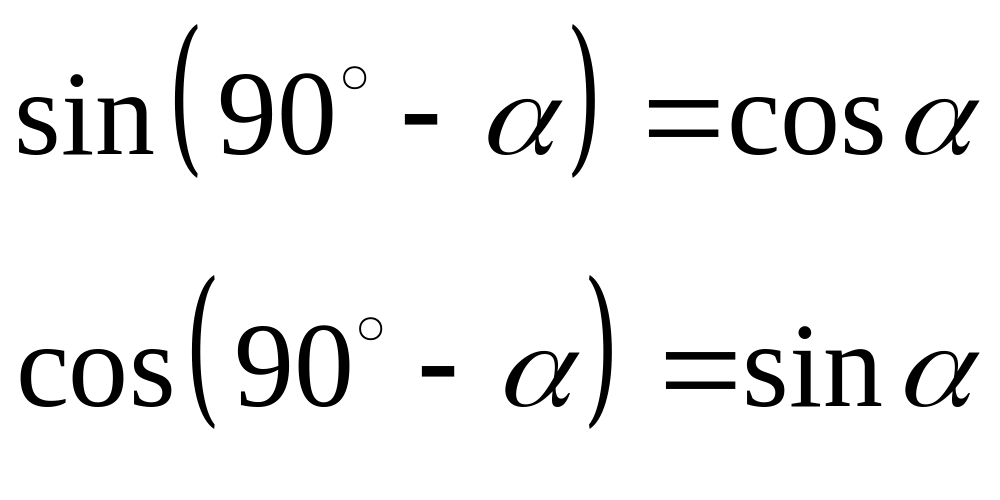
1. Знак результата берется по знаку данной функции в зависимости от четверти.

2. Если острый угол берется при горизонтальном диаметре, т.е. и , то название функции не изменяется; если при вертикальном, т.е. и , то название функции изменяется на сходную.

Например:

Упростить:

1)

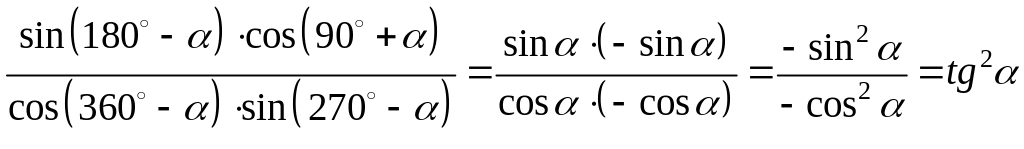
2) Пособие (сборник материалов)

стр. 35 № 8.1; 8.3

стр. 36 № 17.3; 17.4

Самостоятельно:

Упростить:

1)

2)