Пример реализации

Пассивный аналоговый фильтр верхних частот первого порядка, реализованный в виде RC-цепочки

Простейший электронный фильтр верхних частот состоит из последовательно соединённых конденсатора и резистора. Конденсатор пропускает лишь переменный ток, а выходное напряжение снимается с резистора. Произведение сопротивления на ёмкость (R×C) является постоянной времени для такого фильтра, которая обратно пропорциональна частоте среза в герцах:

Применения

Подобный фильтр используется для выделения высоких частот из сигнала и часто используется в обработке аудиосигналов, например в кроссоверах. Ещё одно важное применение фильтра верхних частот — устранение лишь постоянной составляющей сигнала (см. Ёмкостная связь (англ.)русск.), для чего частоту среза выбирают достаточно низкой.

Фильтры верхних частот используются в простых бестрансформаторных конденсаторных преобразователях напряжения для понижения напряжения переменного тока. К недостаткам таких преобразователей относится их высокая чувствительность к импульсным помехам в источнике переменного тока, а также зависимость выходного напряжения от импеданса нагрузки^[1].

Фильтры верхних частот используются в обработке изображений для того, чтобы осуществлять преобразования в частотной области (например, для выделения границ).

Используется также последовательное включение фильтра верхних частот с фильтром нижних частот (ФНЧ). Если при этом частота среза ФВЧ меньше, чем частота среза ФНЧ (то есть, имеется диапазон частот, в котором оба фильтра пропускают сигнал), получится полосовой фильтр (используется для выделения из сигнала определённой полосы частот).

Полосно-пропускающий фильтр — фильтр, который пропускает частоты, находящиеся в некоторой полосе частот.

Полосовой фильтр — линейная система и может быть представлен в виде последовательности, состоящей из фильтра нижних частот и фильтра верхних частот.

Идеальные полосовые фильтры характеризуются двумя характеристиками

• нижняя частота среза ;

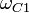• верхняя частота среза .

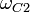В свою очередь, реализация полосового фильтра характеризуется шестью характеристиками

• нижняя граница частоты пропускания ;

• верхняя граница частоты пропускания .

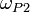• нижняя граница частоты задержания ;

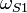• верхняя граница частоты задержания ;

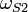а также

• максимальное подавление в полосе пропускания ;

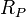• минимальное подавление в полосе подавления .

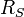Примером реализации такого фильтра может служить колебательный контур (цепь из последовательно соединенных резистора, конденсатора и индуктивности).

Электрическая принципиальная схема полосно-пропускающего фильтра

Полосно-заграждающий фильтр (проф. жаргон — режекторный фильтр) — электронный или любой другой фильтр, не пропускающий колебания некоторой определённой полосы частот, и пропускающий колебания с частотами, выходящими за пределы этой полосы.Эта полоса подавления характеризуется шириной BW и расположена приблизительно вокруг центральной частоты ω0 (рад/с), или fо=ω0/2•3,14 (Гц).Для реальной амплитудно-частотной характеристики частоты ωL и ωU представляют собой нижнюю и верхнюю частоты среза. Заграждающий фильтр, предназначенный для подавления одной определённой частоты, называется узкополосным заграждающим фильтром или фильтром-пробкой (англ. notch filter).

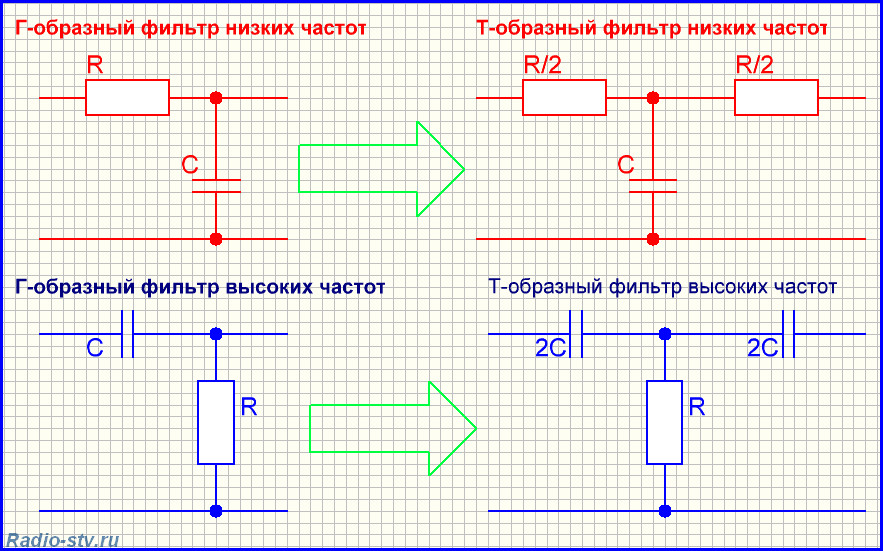
В зависимости от схемы различают фильтры из Г-образных, Т-образных и П-образных звеньев.

Г – образный фильтр

Г-образный фильтр – это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений:

С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня.

Т – образный фильтр

Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:

П – образный фильтр

П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных. Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.

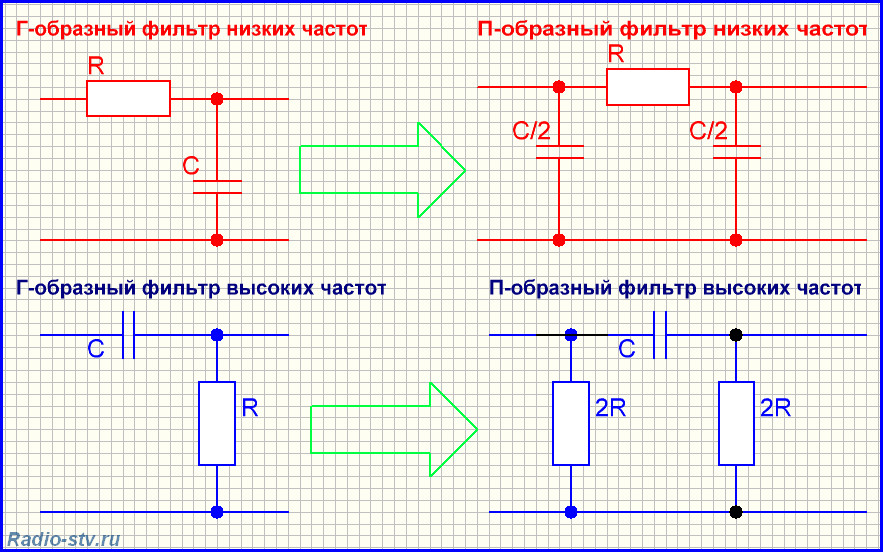
Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов.

По числу звеньев различают фильтры однозвенные (простейшие) и многозвенные. Звенья содержат последовательные и параллельные ветви. Простейшим является Г-образное звено, которое содержит два сопротивления. Особенностью такого звена является невозможность сделать равными (симметричными) сопротивления фильтров со стороны входных (1-1) и выходных (2-2) клемм. Чаще применяют симметричные Т- и П-образные звенья. Они создаются последовательным соединением двух Г-образных звеньев.

В зависимости от вида используемых элементов различают фильтры, содержащие индуктивности и емкости - реактивные фильтры, емкости и активные сопротивления - безиндуктивные или RC-фильтры, фильтры, состоящие из кварцевых пластин (резонаторов) - пьезоэлектрические фильтры.

Фильтр Чебышева — один из типов линейных аналоговых или цифровых фильтров, отличительной особенностью которого является более крутой спад амплитудно-частотной характеристики (АЧХ) и существенные пульсации амплитудно-частотной характеристики на частотах полос пропускания (фильтр Чебышева I рода) и подавления (фильтр Чебышева II рода), чем у фильтров других типов. Фильтр получил название в честь известного русского математика XIX века Пафнутия Львовича Чебышева, так как характеристики этого фильтра основываются на многочленах Чебышева.

Фильтры Чебышева обычно используются там, где требуется с помощью фильтра небольшого порядка обеспечить требуемые характеристики АЧХ, в частности, хорошее подавление частот из полосы подавления, и при этом гладкость АЧХ на частотах полос пропускания и подавления не столь важна.

Различают фильтры Чебышева I и II родов.