Динамические характеристики

Разностное уравнение, описывающее связь между входным и выходным сигналами фильтра: где — порядок фильтра, — входной сигнал, — выходной сигнал, а — коэффициенты фильтра. Иными словами, значение любого отсчета выходного сигнала определяется суммой масштабированных значений предыдущих отсчетов. Можно сказать иначе: значение выхода фильтра в любой момент времени есть значение отклика на мгновенное значение входа и сумма всех постепенно затухающих откликов предыдущих отсчетов сигнала, которые всё ещё оказывают влияние на выход (после -отсчетов импульсная переходная функция становится равной нулю, как уже было сказано, поэтому все члены после -го тоже станут равными нулю). Запишем предыдущее уравнение в более ёмком виде:

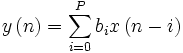
Для того, чтобы найти ядро фильтра положим

где — дельта-функция. Тогда импульсная характеристика КИХ-фильтра может быть записана как:

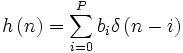
Z-преобразование импульсной характеристики даёт нам передаточную функцию КИХ-фильтра:

Свойства

КИХ-фильтр обладает рядом полезных свойств, из-за которых он иногда более предпочтителен в использовании, чем БИХ-фильтр. Вот некоторые из них:

• КИХ-фильтры устойчивы.

• КИХ-фильтры при реализации не требуют наличия обратной связи.

• Фаза КИХ-фильтров может быть сделана линейной

Прямая форма ких фильтра

КИХ фильтры могут быть реализованы с использованием трех элементов: умножитель, сумматор и блок задержки. Вариант, показанный на рисунке, есть прямая реализация КИХ-фильтров типа 1.

Реализация прямой формы КИХ фильтра

Электрические фильтры могут быть классифицированы по различным признакам: пропускаемым частотам, схемам соединения элементов, типам элементов, характеристикам.

В зависимости от полосы пропускаемых частот различают фильтры нижних частот (ФНЧ), фильтры верхних частот (ФВЧ), полосовые фильтры (ПФ), режекторные (заградительные) фильтры (РФ).

Фильтр ни́жних часто́т (ФНЧ) — один из видов аналоговых или электронных фильтров, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.

В отличие от фильтра нижних частот (НЧ), фильтр верхних частот пропускает частоты сигнала выше частоты среза, подавляя низкие частоты.

Реализация фильтров нижних частот может быть разнообразной, включая электронные схемы, программные алгоритмы, акустические барьеры, механические системы и т. д.

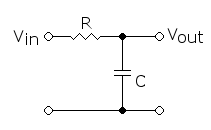
электронный фильтр нижних частот, построенный в виде RC-цепочки

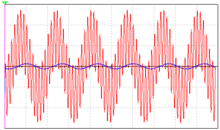
Осциллограмма простейшего RC фильтра нижних частот

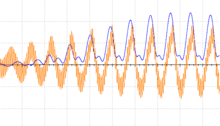
Осциллограмма низкочастотного фильтра Бесселя

В схемах пассивных аналоговых фильтров используют реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя такие элементы, можно добиться усиления или ослабления гармоник с нужными частотами.

Идеальный фильтр нижних частот

Идеальный фильтр нижних частот (sinc-фильтр) полностью подавляет все частоты входного сигнала выше частоты среза и пропускает без изменений все частоты ниже частоты среза. Переходной зоны между частотами полосы подавления и полосы пропускания не существует. Идеальный фильтр нижних частот может быть реализован лишь теоретически с помощью умножения входного сигнала на прямоугольную функцию в частотной области, или, что даёт тот же эффект, свёртки сигнала во временно́й области с sinc-функцией.

Однако такой фильтр практически нереализуем для большинства сигналов, так как sinc-функция имеет ненулевые значения для всех моментов времени вплоть до бесконечности. Его можно использовать только для уже записанных цифровых сигналов либо для идеально периодических сигналов.

Реальные фильтры для приложений реального времени могут лишь приближаться к идеальному фильтру.

Фильтр верхних частот (ФВЧ) — электронный или любой другой фильтр, пропускающий высокие частоты входного сигнала, при этом подавляя частоты сигнала ниже частоты среза. Степень подавления зависит от конкретного типа фильтра.

Термины «высокие частоты» и «низкие частоты» в применении к фильтрам относительны и зависят от выбранной структуры и параметров фильтра.