] Пример
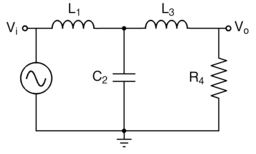
Аналоговый фильтр Баттерворта нижних
частот (топология Кауэра) с частотой
среза
со
следующими номиналами элементов:
фарад,
ом,
и
генри.
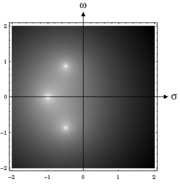
Логарифмический график плотности передаточной функции H(s) на плоскости комплексного аргумента для фильтра Баттерворта третьего порядка с частотой среза . Три полюса лежат на круге единичного радиуса в левой полуплоскости.
Рассмотрим аналоговый низкочастотный
фильтр Баттерворта третьего порядка с
фарад,
ом,
и
генри.
Обозначив полное
сопротивление ёмкостей C
как 1/Cs и полное сопротивление
индуктивностей L как Ls, где
—
комплексная переменная, и используя
уравнения
для расчёта электрических схем,
получим следующую передаточную функцию
для такого фильтра:
АЧХ задаётся уравнением:
а ФЧХ задаётся уравнением:
Групповая
задержка определяется как
минус производная фазы по круговой
частоте и является мерой искажений
сигнала по фазе на различных частотах.
Логарифмическая
АЧХ
такого
фильтра не имеет пульсаций ни в полосе
пропускания, ни в полосе подавления.
График модуля передаточной функции на комплексной плоскости ясно указывает на три полюса в левой полуплоскости. Передаточная функция полностью определяется расположением этих полюсов на единичном круге симметрично относительно действительной оси.
Заменив каждую индуктивность ёмкостью, а ёмкости — индуктивностями, получим высокочастотный фильтр Баттерворта.
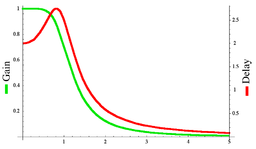
и групповая задержка фильтра Баттерворта третьего порядка с частотой среза