4.Основные теоретические положения

На практике бывает потребность в устройствах, которые при относительно небольшом потенциале окружающих тел накапливали бы на себе («конденсировали») заметные по величине заряды. В основу таких устройств, которые называются конденсаторами, положен тот факт, что электроемкость проводника возрастает при приближении к нему других тел.

Это вызвано тем, что под действием поля, создаваемого заряженным проводником, на поднесенном к нему теле возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды. Заряды, противоположные по знаку заряду проводника q, располагаются ближе к проводнику, чем одноименные с q, и, следовательно, оказывают большое внимание на его потенциал. Поэтому, при поднесении к заряженному проводнику какого-либо тела, потенциал проводника уменьшается по абсолютной величине, что означает увеличение емкости проводника.

Конденсаторы делают в виде двух проводников, помещенных близко друг к другу. Образующие конденсатор проводники называют его обкладками. Чтобы внешние тела не оказывали влияния на емкость конденсатора, обкладкам придают такую форму и так располагают их друг относительно друга, чтобы поле, создаваемое накапливаемыми на них зарядами, было сосредоточено внутри конденсатора. Этому условию удовлетворяют две пластинки, расположенные близко друг к другу, два коаксиальных цилиндра и две концентрические сферы. Соответственно бывают плоские, цилиндрические и сферические конденсаторы. Поскольку поле заключено внутри конденсатора, линии электрического смещения начинаются на одной обкладке и заканчиваются на другой. Следовательно, сторонние заряды, возникающие на обкладках, имеют одинаковую величину и различны по знаку.

Основной характеристикой конденсатора является его емкость, под которой понимают величину, пропорциональную заряду q и обратно пропорциональную разности потенциалов между обкладками:

;

Разность потенциалов называют напряжением между соответствующими точками и обозначают U.

Воспользовавшись этим обозначением, можно придать этой формуле следующий вид:

; где U- напряжение между обкладками.

Рассмотрим заряженную частицу, попадающую в электрическое поле заряженного конденсатора, (рис. 2). Определим смещение частицы, вызываемое перпендикулярным к ней однородным электрическим полем, действующим на пути длиной l₁.

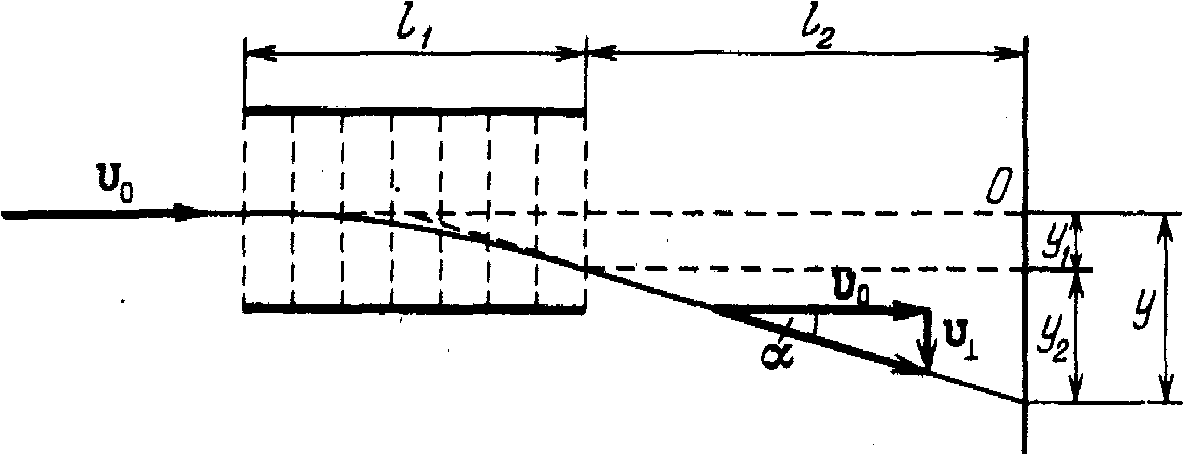
Рис.2

Пусть первоначально скорость частицы равна V0. Войдя в область поля, она будет двигаться с постоянным по величине и направлению, перпендикулярным к V₀ ускорением w_=(е'/т)*Е (е'/т — удельный заряд частицы).

Движение под действием поля продолжается время t= l₁/V₀. За это время частицы сместятся на расстояние.

_

и приобретут перпендикулярную к V₀ составляющую скорости:

V_=w_t=

В дальнейшем частица летит прямолинейно в направлении, которое образует с вектором V₀ угол а, определяемый соотношением:

tg=

Таким образом, смещение частицы относительно точки О равно

Приняв во внимание формулу tg= , выражению для смещения можно придать вид:

При неравномерном движении частицы по кри­волинейной траектории ускорение распадается на два слагаемых. Одно из них коллинеарно скорости и, следовательно, направлено по касатель­ной к траектории. Поэтому его называют тангенциальным (т. е. касательным) ускорением и обозначают а_. Второе слагаемое определяется формулой и является нор­мальным ускорением.

Итак, Первое слагаемое характеризует быстроту изменения модуля скорости, второе слагае­мое — быстроту изменения направления скорости.

Составляющие а_ и а_п перпендикулярны друг к другу. Поэтому квадрат модуля ускорения равен сум­ме квадратов модулей составляющих: Отсюда следует, что

5.Определение параметров частицы

Дано:

q=3*1,6*10^-19Кл

m=10*1,66*10^-27кг

Е₀=20 кэВ=1.6*10^-19*20 Дж=32*10^-19 Дж

V₀=?

Решение:

Начальная кинетическая энергия:

6.Определение параметров конденсатора:

Дано:

l=25см=0,25м

Q=0.3 мкКл

U=12кВ

W-? Дж

С-? Ф

d-? мм

Решение:

, т.к. конденсатор заполнен воздухом =1, а =8,85*10^-12Ф/м (диэлектрическая проницаемость вакуума), S=0,25²м²=0,0625 м²

7.Расчет графической зависимости R(t):

1. Н

P=mg= Н

= Н

м/с

м/c²

м/с

График 1. Зависимость радиуса кривизны траектории частицы от времени полета в конденсаторе

8.График зависимости E(t)

9.Вывод.

В расчетно-графическом задании «Движение заряженной частицы в электрическом поле» рассматривалось движение иона гелия ¹⁰B³⁺ в однородном электрическом поле между обкладками заряженного конденсатора. Для выполнения задания я ознакомился с устройством и основными характеристиками конденсатора, так же изучил движение заряженной частицы в однородном магнитном поле, а также движение материальной точки по криволинейной траектории и рассчитал необходимые по заданию параметры частицы и конденсатора.