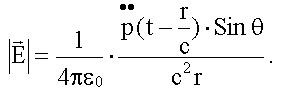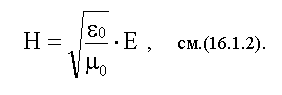- •3. Элементы кинематики
- •3.1. Материальная точка, система материальных точек, абсолютно твердое тело - простейшие физические модели
- •3.1.1. Материальная точка
- •3.1.3. Абсолютно твердое тело
- •3.2. Тело отсчета
- •3.3. Система отсчета
- •3.8.1. Скорость направлена по касательной к траектории
- •3.8.2. Компоненты скорости
- •3.9. Вычисление пройденного пути
- •3.10.1. Нормальное и тангенциальное ускорение
- •6. Кинематика вращательного движения
- •6.1. Поступательное и вращательное движение
- •6.2. Псевдовектор бесконечно малого поворота
- •6.5. Связь линейной скорости материальной точки твердого тела и угловой скорости
- •4. Динамика материальной точки
- •4.6.1. Система си (System international)
- •4.6.1.1. Размерность силы
- •4.7. Третий закон Ньютона
- •5. Законы сохранения
- •5.1. Механическая система - это совокупность тел, выделенных нами для рассмотрения 5.1.1. Внутренние и внешние силы
- •5.2. Закон сохранения импульса
- •5.6.1. Консервативность силы тяжести
- •5.6.2. Неконсервативность силы трения
- •5.7. Потенциальная энергия может быть введена только для поля консервативных сил
- •5.8.Закон сохранения механической энергии
- •7. Динамика вращательного движения
- •8. Элементы специальной теории относительности
- •8.2. Принцип относительности Галилея:
- •8.3. Неудовлетворительность механики Ньютона при больших скоростях
- •Принцип постоянства скорости света:
- •8.5.1. Вывод преобразований Лоренца
- •Электричество
- •9. Постоянное электрическое поле
- •9.3. Электрическое поле
- •9.3.6. Принцип суперпозиции электрических полей
- •9.3.7. Напряженность поля точечного заряда
- •9.3.8. Линии напряженности
- •9.4.2.2. Заряд в произвольном месте внутри сферы
- •9.4.2.4. Поток вектора е поля системы зарядов, находящихся внутри замкнутой поверхности
- •9.4.2.5. Поток вектора е для поля, созданного зарядами, находящимися вне замкнутой поверхности
- •9.4.3. Формулировка теоремы Гаусса
- •9.4.4.1. Поле равномерно заряженной бесконечной плоскости
- •9.9. Проводник в электрическом поле
- •9.10. Электроемкость уединенного проводника
- •9.11. Электроемкость конденсатора
- •9.12. Энергия электрического поля
- •9.12.1. Плотность энергии электрического поля в вакууме
- •9.13. Электрическое поле в диэлектрике
- •9.13.1. Диэлектрик?
- •9.13.1.1. Два типа диэлектриков - полярные и неполярные
- •9.13.2. Поляризованность диэлектрика (вектор поляризации) - это дипольный момент единицы объема:
- •9.13.4.1. Плотность энергии электрического поля в диэлектрике
- •10. Постоянный электрический ток
- •10.1. Сила тока
- •10.2. Плотность тока
- •10.2.1. Связь плотности тока и скорости упорядоченного движения зарядов
- •10.4. Закон Ома для участка цепи
- •10.5. Закон Ома в дифференциальной форме
- •10.6. Закон Джоуля-Ленца в дифференциальной форме
- •Магнетизм. Уравнения Максвелла
- •11. Магнитное поле в вакууме
- •11.2. Проводник с током создает только магнитное поле, другой проводник с током реагирует только на магнитное поле
- •11.3. Рамка с током как регистратор магнитного поля. Вектор магнитной индукции
- •11.5.6. Магнитное поле тороида
- •11.6. Закон Ампера
- •11.7. Сила Лоренца - это сила, действующая со стороны магнитного поля на движущийся в нем заряд
- •11.7.1. Движение заряженной частицы в однородном магнитном поле
- •11.11.1. Потокосцепление
- •11.11.2. Индуктивность соленоида
- •11.11.3. Энергия магнитного поля
- •12. Магнитное поле в веществе
- •12.2. Классификация магнетиков
- •13. Уравнения Максвелла
- •13.1. Первая пара уравнений Максвелла в интегральной форме
- •13.1.1. Первое уравнение первой пары - это закон Фарадея-Ленца
- •13.1.2. Второе уравнение первой пары - нет магнитных зарядов
- •13.2. Вторая пара уравнений Максвелла в интегральной форме
- •13.3. Система уравнений Максвелла в интегральной форме
- •13.4. Система уравнений Максвелла в дифференциальной форме
- •Литература,
- •А.Н. Тюшев
- •В конспективном изложении
- •Колебания. Волны. Волновая оптика
- •Электронная версия учебного издания
- •14.1.1.4. График гармонического колебания
- •14.2 Дифференциальное уравнение гармонических колебаний
- •14.2.1 Колеблющиеся системы
- •14.3.2. Сложение колебаний одинаковой частоты и одинакового направления
- •14.3.3. Сложение колебаний близких частот
- •14.3.4. Сложение взаимно-перпендикулярных колебаний
- •14.4. Затухающие колебания
- •14.4.1. Колеблющиеся системы
- •14.4.5. Дифференциальное уравнение, описывающее затухающие колебания наших двух систем в этих обозначениях будет иметь один и тот же вид
- •14.4.6. Решение
- •14.4.7. Проверка
- •14.5.5. Дифференциальное уравнение, описывающее вынужденные колебания
- •14.5.6. Решение дифференциального уравнения
- •14.5.6.1. Частное решение неоднородного уравнения
- •14.5.6.1.1. Векторная диаграмма
- •14.5.6.1.2. Резонанс
- •16. Электромагнитные волны
- •16.1. Система уравнений Максвелла для плоской электромагнитной волны
- •16.1.1. Поперечность электромагнитных волн
- •16.1.2. Волновое уравнение
- •16.5.1.1. Вероятностное истолкование электромагнитной волны
- •17. Геометрическая оптика
- •17.1. Законы геометрической оптики
- •17.1.1. Закон прямолинейного распространения света
- •17.1.2. Закон независимости световых лучей
- •17.1.3. Законы отражения и преломления
- •17.2. Полное внутреннее отражение
- •17.3. Тонкие линзы
- •17.3.1. Собирающие и рассеивающие линзы
- •17.3.2. Фокусы линзы, фокальная плоскость
- •17.3.3. Фокусное расстояние тонкой линзы
- •17.3.4. Построение изображения в линзах
- •18.2. Способы получения когерентных источников
- •18.2.1. Опыт Юнга
- •18.2.2. Зеркала Френеля
- •18.2.3. Бипризма Френеля
- •18.2.4. Интерференция при отражении от прозрачных пластинок
- •18.2.4.1. Кольца Ньютона
- •18.3. Многолучевая интерференция
- •19. Дифракция света
- •19.1 Дифракция Френеля и Фраунгофера
- •19.2. Принцип Гюйгенса-Френеля
- •19.2.1. Математическая формулировка принципа Гюйгенса-Френеля
- •19.3. Зоны Френеля
- •19.3.1. Дифракция Френеля на круглом отверстии
- •19.3.2. Дифракция Фраунгофера на щели
- •19.3.2.1. Таутохронность линзы и ее следствия
- •19.3.2.2. Определение положений максимумов и минимумов методом зон Френеля
- •19.3.2.3. Зависимость интенсивности дифракционной картины от угла дифракции φ
- •19.4 Дифракционная решетка
- •19.4.1. Условие главного максимума для дифракционной решетки
- •19.4.2. Зависимость интенсивности дифракционной картины решетки от угла дифракции φ
- •19.4.2.1. Минимумы интенсивности дифракционной картины решетки
- •19.4.2.2. Добавочные минимумы, ближайшие к главным максимумам
- •19.4.3. График интенсивности Ip(Sinφ )
- •19.4.4. Дифракционная решетка как спектральный прибор
- •19.4.4.1. Угловая дисперсия дифракционной решетки
- •19.4.4.2. Линейная дисперсия
- •19.4.4.3. Разрешающая сила дифракционной решетки
- •19.4.4.3.1. Критерий Релея
- •19.4.4.4. Разрешающая сила решетки для цуга волн. Соотношение между длиной цуга δx и точностью определения волнового числа δk.
- •20. Поляризация света
- •20.1. Плоско поляризованная электромагнитная волна
- •20.2. Принцип действия поляризатора электромагнитной волны
- •20.2.1. Поляроид
- •20.3. Закон Малюса
- •20.3.1. Частично поляризованный свет. Степень поляризации
- •20.4. Эллиптическая и круговая поляризация
- •20.5. Поляризация при отражении и преломлении
- •20.5.1. Формулы Френеля
- •20.5.2. Закон Брюстера
- •20.6. Двойное лучепреломление
- •20.6.1. Модель двояко преломляющего кристалла
- •20.6.1.1. Необыкновенный и обыкновенный луч
- •21. Взаимодействие света с веществом
- •21.1. Дисперсия света
- •21.1.1. Классическая электронная теория дисперсии
- •21.1.1.1. Связь показателя преломления с дипольным моментом молекулы
- •21.1.1.2. Связь дипольного момента молекулы с напряженностью поля световой волны
- •21.1.1.2.1. Простейшая модель атома в поле световой волны
- •21.1.1.2.2. Уравнение движения электрона и его решение
- •21.1.1.2.3. Проекции дипольного момента и напряженности поля волны на ось X
- •21.1.1.3. Выражение для n2
- •21.1.1.4. Анализ зависимости n(ω)
- •21.2.1. Связь групповой скорости u с фазовой скоростью V
- •Список литературы, использованный при написании II части конспекта лекций по физике
16. Электромагнитные волны
Выпишем здесь еще раз систему уравнений Максвелла в дифференциальной форме вместе с материальными уравнениями (15.3):
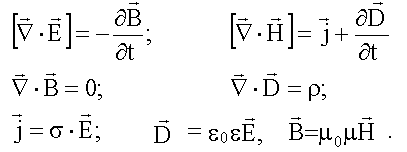
Применим систему уравнений Максвелла (13.4) к однородной ( ε = const, μ = const), нейтральной ( ρ = 0), непроводящей ( σ = 0) среде. Уравнения Максвелла примут следующий вид.
Первая пара:
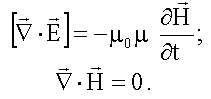
Вторая пара:
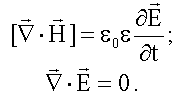
Наша задача -
получить волновые уравнения для векторов
![]() и
и
![]() ,
решениями которых будут уравнения
электромагнитной волны
,
решениями которых будут уравнения
электромагнитной волны
![]() (сравните
с 15.3).
(сравните
с 15.3).
16.1. Система уравнений Максвелла для плоской электромагнитной волны
Зададим направление оси x перпендикулярно волновым поверхностям. Тогда:
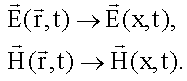
От координат x и z в плоской волне и не зависят. Как известно из математики:
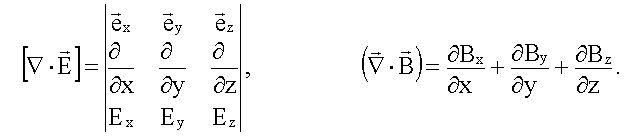
Учитывая, что не зависит от y и z из первого уравнения первой пары:
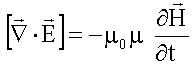 ,
,
получим три скалярных уравнения:
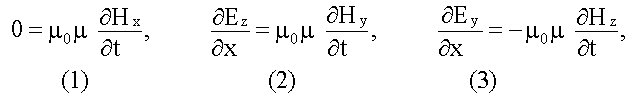
Второе уравнение первой пары дает:
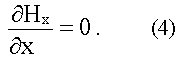
Аналогично, из второй пары уравнений Максвелла получим:
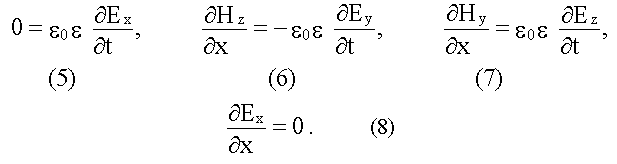
16.1.1. Поперечность электромагнитных волн
Уравнения (1) и (4), (5) и (8) утверждают, что Hx и Ex не зависят от времени и координаты x, т.е. являются однородными постоянными полями. Таким образом, переменное поле электромагнитной волны не имеет составляющей вдоль оси x, в направлении которой распространяется волна. Это значит, что электромагнитная волна поперечна, т.е. векторы и перпендикулярны направлению ее распространения.
16.1.2. Волновое уравнение
В уравнения (2) и (7) входят Ez и Hy, в уравнения (3) и (6) входят Ey и Hz. Таким образом, если первоначально было создано поле Ey, то оно породит Hz (3), которое создает Ey (6). Аналогично с Ez и Hy.
Для описания электромагнитной волны можно выбрать уравнения (2) и (7), либо уравнения (3) и (6), либо те и другие.
Получим волновое уравнение для уравнений (3) и (6):
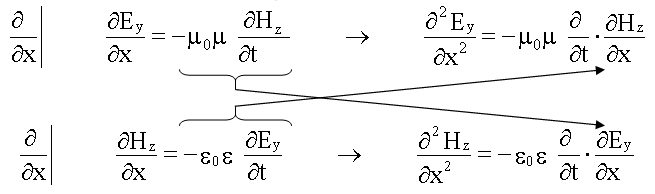
После указанных стрелками замен имеем два волновых уравнения:
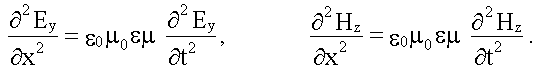
16.1.2.1. Фазовая скорость электромагнитной волны
Коэффициент при второй производной по времени, есть величина, обратная квадрату фазовой скорости волны (см. 15.3.2). Для электромагнитной волны фазовая скорость из волновых уравнений 16.1.2:
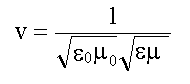
В вакууме ε = &mu = 1 и
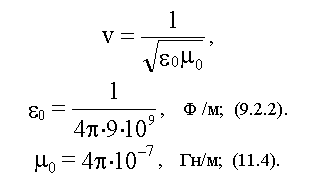 .
.
Тогда:
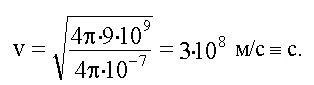
Полученное значение фазовой скорости электромагнитной волны в вакууме равно скорости света в вакууме - с. С учетом этого:
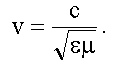
16.1.2.2. Гармонические волны - простейшие решения волновых уравнений
Легко проверить, что
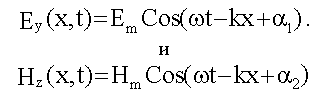
являются решениями
волновых уравнений (16.1.2).
Эти решения описывают электромагнитную
волну, у которой вектор
направлен
вдоль оси y,
вектор
-
вдоль оси z,
волна распространяется вдоль оси x,
таким образом, векторы
,
,
![]() образуют
правую тройку.
образуют
правую тройку.
16.1.2.3. Связь между модулями векторов и электромагнитной волны и их фазами
Подставив решения (16.1.2.2.) в уравнения (3) и (6), получим из (3):
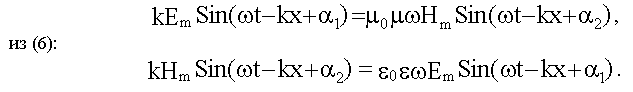
Из этих равенств следует:
1) Векторы и колеблются в одинаковой фазе.
![]() ;
;
2)

16.2. Пространственная структура электромагнитной волны
Для фиксированного момента времени t1 векторы и плоской гармонической электромагнитной волны могут быть изображены следующей диаграммой:
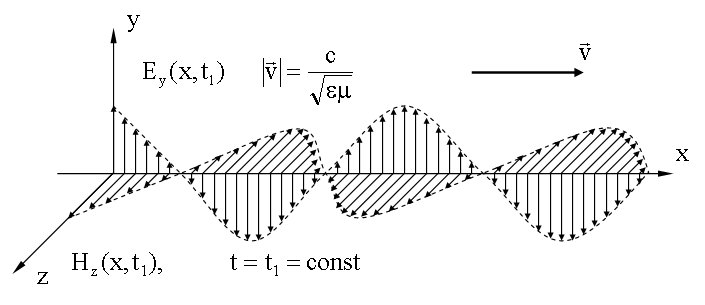
16.3. Плотность энергии электромагнитной волны
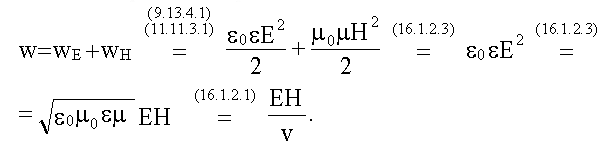
16.3.1. Вектор Пойнтинга - вектор плотности потока энергии электромагнитной волны
Из (15.4.4):
![]() .
.
Для электромагнитной
волны вектор плотности потока энергии
обозначают буквой
![]() .
.
Из (16.3):
![]() .
.
Используя диаграмму (16.2) величине S можно придать векторный характер:
![]()
16.3.2. Интенсивность электромагнитной волны - это среднее по времени от модуля вектора Пойнтинга
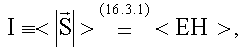
сравните с (15.4.5).
16.4. Изучение диполя
16.4.1. Диполь
- это два разноименных точечных заряда, находящихся на некотором расстоянии друг от друга (см. 9.13.1.1).
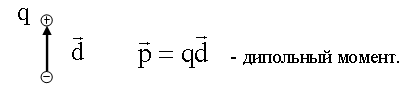
16.4.2. Электрическое и магнитное поле колеблющегося диполя
Пусть расстояние
между зарядами диполя периодически
изменяется с течением времени, т.е.
![]() ,
диполь колеблется. Тогда
,
диполь колеблется. Тогда ![]() .
.
Электрическое и магнитное поле диполя будет переменным, диполь будет излучать электромагнитные волны.
|
|
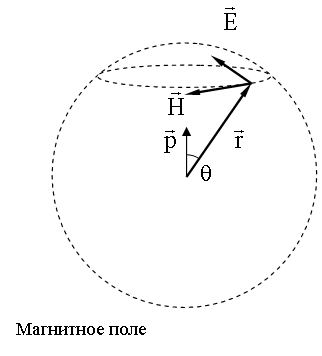
Точный расчет на основе уравнений Максвелла показывает, что электрическое поле в этой волне, распространяющейся в вакууме:
Направление
векторов
и
изображено
на рисунке. Угол θ - это угол между
направлением дипольного момента
|
16.4.2.1. Электрическое поле диполя, колеблющегося по гармоническому закону
Пусть
![]() ,
тогда:
,
тогда:
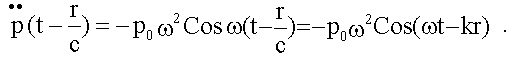
Для E из (16.4.2) имеем:
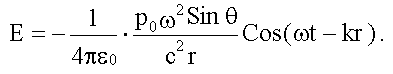
16.4.2.2. Интенсивность дипольного гармонического излучения
Из (16.3.2):
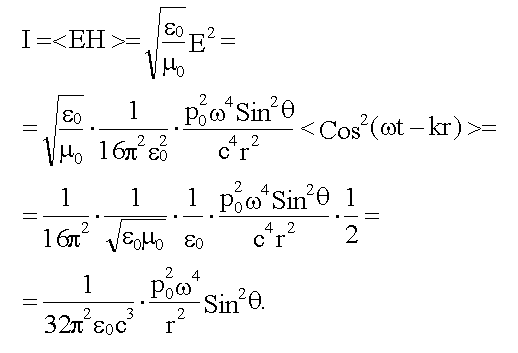
16.4.2.3. Диаграмма направленности излучения диполя
- это графическое изображение в полярной системе координат зависимости интенсивности излучения I, (16.4.2.2), от угла θ.
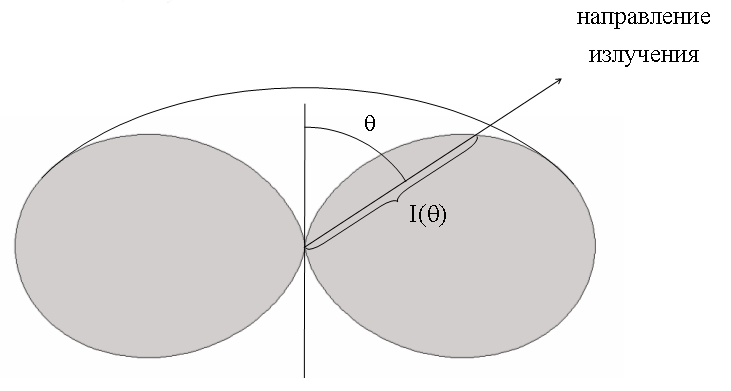
На рисунке дана половина пространственного изображения диаграммы направленности. Полная диаграмма похожа на бублик без дырки.
16.5. Световые волны
Световая волна - это электромагнитная волна с длиной волны в вакууме:
![]()
Волны такого диапазона воспринимаются человеческим глазом. Частота световой волны (15.1.8.), (16.1.2.1.):
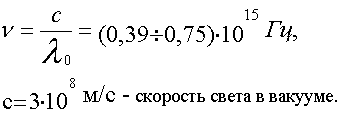
16.5.1. Современная точка зрения на природу света
По современным
представлениям свет - это поток фотонов,
т.е. элементарных частиц, имеющих нулевую
массу, двигающихся со скоростью
![]() м/с.
Каждый фотон (квант света) обладает
энергией:
м/с.
Каждый фотон (квант света) обладает
энергией:
![]() ,
,
где v - частота
электромагнитной волны, ![]() - постоянная Планка. (М. Planck - немецкий
физик, получивший в 1900 году на основе
выдвинутой им гипотезы квантов, закон
распределения в спектре излучения
абсолютно черного тела).
- постоянная Планка. (М. Planck - немецкий
физик, получивший в 1900 году на основе
выдвинутой им гипотезы квантов, закон
распределения в спектре излучения
абсолютно черного тела).
Импульс каждого фотона:
![]() ,
,
где ![]() - волновой вектор (15.2.4),
модуль волнового вектора (см. 15.2.4.1).
- волновой вектор (15.2.4),
модуль волнового вектора (см. 15.2.4.1).
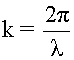 .
.