- •3. Элементы кинематики
- •3.1. Материальная точка, система материальных точек, абсолютно твердое тело - простейшие физические модели
- •3.1.1. Материальная точка
- •3.1.3. Абсолютно твердое тело
- •3.2. Тело отсчета
- •3.3. Система отсчета
- •3.8.1. Скорость направлена по касательной к траектории
- •3.8.2. Компоненты скорости
- •3.9. Вычисление пройденного пути
- •3.10.1. Нормальное и тангенциальное ускорение
- •6. Кинематика вращательного движения
- •6.1. Поступательное и вращательное движение
- •6.2. Псевдовектор бесконечно малого поворота
- •6.5. Связь линейной скорости материальной точки твердого тела и угловой скорости
- •4. Динамика материальной точки
- •4.6.1. Система си (System international)
- •4.6.1.1. Размерность силы
- •4.7. Третий закон Ньютона
- •5. Законы сохранения
- •5.1. Механическая система - это совокупность тел, выделенных нами для рассмотрения 5.1.1. Внутренние и внешние силы
- •5.2. Закон сохранения импульса
- •5.6.1. Консервативность силы тяжести
- •5.6.2. Неконсервативность силы трения
- •5.7. Потенциальная энергия может быть введена только для поля консервативных сил
- •5.8.Закон сохранения механической энергии
- •7. Динамика вращательного движения
- •8. Элементы специальной теории относительности
- •8.2. Принцип относительности Галилея:
- •8.3. Неудовлетворительность механики Ньютона при больших скоростях
- •Принцип постоянства скорости света:
- •8.5.1. Вывод преобразований Лоренца
- •Электричество
- •9. Постоянное электрическое поле
- •9.3. Электрическое поле
- •9.3.6. Принцип суперпозиции электрических полей
- •9.3.7. Напряженность поля точечного заряда
- •9.3.8. Линии напряженности
- •9.4.2.2. Заряд в произвольном месте внутри сферы
- •9.4.2.4. Поток вектора е поля системы зарядов, находящихся внутри замкнутой поверхности
- •9.4.2.5. Поток вектора е для поля, созданного зарядами, находящимися вне замкнутой поверхности
- •9.4.3. Формулировка теоремы Гаусса
- •9.4.4.1. Поле равномерно заряженной бесконечной плоскости
- •9.9. Проводник в электрическом поле
- •9.10. Электроемкость уединенного проводника
- •9.11. Электроемкость конденсатора
- •9.12. Энергия электрического поля
- •9.12.1. Плотность энергии электрического поля в вакууме
- •9.13. Электрическое поле в диэлектрике
- •9.13.1. Диэлектрик?
- •9.13.1.1. Два типа диэлектриков - полярные и неполярные
- •9.13.2. Поляризованность диэлектрика (вектор поляризации) - это дипольный момент единицы объема:
- •9.13.4.1. Плотность энергии электрического поля в диэлектрике
- •10. Постоянный электрический ток
- •10.1. Сила тока
- •10.2. Плотность тока
- •10.2.1. Связь плотности тока и скорости упорядоченного движения зарядов
- •10.4. Закон Ома для участка цепи
- •10.5. Закон Ома в дифференциальной форме
- •10.6. Закон Джоуля-Ленца в дифференциальной форме
- •Магнетизм. Уравнения Максвелла
- •11. Магнитное поле в вакууме
- •11.2. Проводник с током создает только магнитное поле, другой проводник с током реагирует только на магнитное поле
- •11.3. Рамка с током как регистратор магнитного поля. Вектор магнитной индукции
- •11.5.6. Магнитное поле тороида
- •11.6. Закон Ампера
- •11.7. Сила Лоренца - это сила, действующая со стороны магнитного поля на движущийся в нем заряд
- •11.7.1. Движение заряженной частицы в однородном магнитном поле
- •11.11.1. Потокосцепление
- •11.11.2. Индуктивность соленоида
- •11.11.3. Энергия магнитного поля
- •12. Магнитное поле в веществе
- •12.2. Классификация магнетиков
- •13. Уравнения Максвелла
- •13.1. Первая пара уравнений Максвелла в интегральной форме
- •13.1.1. Первое уравнение первой пары - это закон Фарадея-Ленца
- •13.1.2. Второе уравнение первой пары - нет магнитных зарядов
- •13.2. Вторая пара уравнений Максвелла в интегральной форме
- •13.3. Система уравнений Максвелла в интегральной форме
- •13.4. Система уравнений Максвелла в дифференциальной форме
- •Литература,
- •А.Н. Тюшев
- •В конспективном изложении
- •Колебания. Волны. Волновая оптика
- •Электронная версия учебного издания
- •14.1.1.4. График гармонического колебания
- •14.2 Дифференциальное уравнение гармонических колебаний
- •14.2.1 Колеблющиеся системы
- •14.3.2. Сложение колебаний одинаковой частоты и одинакового направления
- •14.3.3. Сложение колебаний близких частот
- •14.3.4. Сложение взаимно-перпендикулярных колебаний
- •14.4. Затухающие колебания
- •14.4.1. Колеблющиеся системы
- •14.4.5. Дифференциальное уравнение, описывающее затухающие колебания наших двух систем в этих обозначениях будет иметь один и тот же вид
- •14.4.6. Решение
- •14.4.7. Проверка
- •14.5.5. Дифференциальное уравнение, описывающее вынужденные колебания
- •14.5.6. Решение дифференциального уравнения
- •14.5.6.1. Частное решение неоднородного уравнения
- •14.5.6.1.1. Векторная диаграмма
- •14.5.6.1.2. Резонанс
- •16. Электромагнитные волны
- •16.1. Система уравнений Максвелла для плоской электромагнитной волны
- •16.1.1. Поперечность электромагнитных волн
- •16.1.2. Волновое уравнение
- •16.5.1.1. Вероятностное истолкование электромагнитной волны
- •17. Геометрическая оптика
- •17.1. Законы геометрической оптики
- •17.1.1. Закон прямолинейного распространения света
- •17.1.2. Закон независимости световых лучей
- •17.1.3. Законы отражения и преломления
- •17.2. Полное внутреннее отражение
- •17.3. Тонкие линзы
- •17.3.1. Собирающие и рассеивающие линзы
- •17.3.2. Фокусы линзы, фокальная плоскость
- •17.3.3. Фокусное расстояние тонкой линзы
- •17.3.4. Построение изображения в линзах
- •18.2. Способы получения когерентных источников
- •18.2.1. Опыт Юнга
- •18.2.2. Зеркала Френеля
- •18.2.3. Бипризма Френеля
- •18.2.4. Интерференция при отражении от прозрачных пластинок
- •18.2.4.1. Кольца Ньютона
- •18.3. Многолучевая интерференция
- •19. Дифракция света
- •19.1 Дифракция Френеля и Фраунгофера
- •19.2. Принцип Гюйгенса-Френеля
- •19.2.1. Математическая формулировка принципа Гюйгенса-Френеля
- •19.3. Зоны Френеля
- •19.3.1. Дифракция Френеля на круглом отверстии
- •19.3.2. Дифракция Фраунгофера на щели
- •19.3.2.1. Таутохронность линзы и ее следствия
- •19.3.2.2. Определение положений максимумов и минимумов методом зон Френеля
- •19.3.2.3. Зависимость интенсивности дифракционной картины от угла дифракции φ
- •19.4 Дифракционная решетка
- •19.4.1. Условие главного максимума для дифракционной решетки
- •19.4.2. Зависимость интенсивности дифракционной картины решетки от угла дифракции φ
- •19.4.2.1. Минимумы интенсивности дифракционной картины решетки
- •19.4.2.2. Добавочные минимумы, ближайшие к главным максимумам
- •19.4.3. График интенсивности Ip(Sinφ )
- •19.4.4. Дифракционная решетка как спектральный прибор
- •19.4.4.1. Угловая дисперсия дифракционной решетки
- •19.4.4.2. Линейная дисперсия
- •19.4.4.3. Разрешающая сила дифракционной решетки
- •19.4.4.3.1. Критерий Релея
- •19.4.4.4. Разрешающая сила решетки для цуга волн. Соотношение между длиной цуга δx и точностью определения волнового числа δk.
- •20. Поляризация света
- •20.1. Плоско поляризованная электромагнитная волна
- •20.2. Принцип действия поляризатора электромагнитной волны
- •20.2.1. Поляроид
- •20.3. Закон Малюса
- •20.3.1. Частично поляризованный свет. Степень поляризации
- •20.4. Эллиптическая и круговая поляризация
- •20.5. Поляризация при отражении и преломлении
- •20.5.1. Формулы Френеля
- •20.5.2. Закон Брюстера
- •20.6. Двойное лучепреломление
- •20.6.1. Модель двояко преломляющего кристалла
- •20.6.1.1. Необыкновенный и обыкновенный луч
- •21. Взаимодействие света с веществом
- •21.1. Дисперсия света
- •21.1.1. Классическая электронная теория дисперсии
- •21.1.1.1. Связь показателя преломления с дипольным моментом молекулы
- •21.1.1.2. Связь дипольного момента молекулы с напряженностью поля световой волны
- •21.1.1.2.1. Простейшая модель атома в поле световой волны
- •21.1.1.2.2. Уравнение движения электрона и его решение
- •21.1.1.2.3. Проекции дипольного момента и напряженности поля волны на ось X
- •21.1.1.3. Выражение для n2
- •21.1.1.4. Анализ зависимости n(ω)
- •21.2.1. Связь групповой скорости u с фазовой скоростью V
- •Список литературы, использованный при написании II части конспекта лекций по физике
3. Элементы кинематики
3.1. Материальная точка, система материальных точек, абсолютно твердое тело - простейшие физические модели
3.1.1. Материальная точка
Материальная точка - это одна из простейших физических моделей (1.3).
|
|
|
<> |
|
реальный мир |
|
исследователь |
|
модельный мир |
Тело из реального мира (см. рис.) иногда можно без ущерба для решаемой задачи заменить точкой в модельном мире, сохранив из всех многообразных свойств этого тела лишь два: положение в пространстве и массу. Эти две характеристики легко описать языком физики (1.4). Массу задают числом. Положение - координатами в выбранной системе координат (3.4.1).
Традиционное определение материальной точки: это тело, размерами которого можно пренебречь при описании его движения. Здесь вместе присутствуют понятия, описывающие и реальный мир, и модельный мир.
3.1.2. Система материальных точек Если решается задача о движении нескольких материальных тел и каждое из них можно в условии данной задачи заменить материальной точкой, то моделью этой системы (1.3) будет система материальных точек.
Пример:
|
|
|
<> |
|
реальный мир |
|
исследователь |
|
модельный мир |
3.1.3. Абсолютно твердое тело
Существуют такие задачи, в которых размерами тела нельзя пренебречь, но, в то же время, можно не учитывать изменение со временем размеров, формы тела. При решении таких задач используют модель - абсолютно твердое тело, т.е. реальное тело заменяют таким, у которого размеры и форма не меняются.
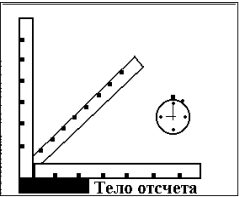
3.2. Тело отсчета
Тело отсчета - это тело, относительно которого определяют положение рассматриваемого нами тела или системы тел.
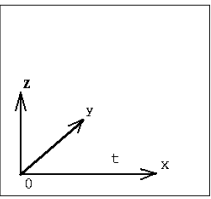
3.3. Система отсчета
Это система координат, связанная с телом отсчета (3.2) и выбранный способ измерения времени (часы).
|
|
|
<> |
|
реальный мир |
|
исследователь |
|
модельный мир |
В реальном трехмерном мире система отсчета - это набор масштабных стержней (или линеек) и часы, расположенные в разных местах этих линеек. В модельном мире система отсчета превращается в трехмерную систему координат, положение которой связано с положением тела отсчета. В каждой точке пространства существует возможность определить время любого происшедшего в этой точке события.
3.4. Положение материальной точки в пространстве
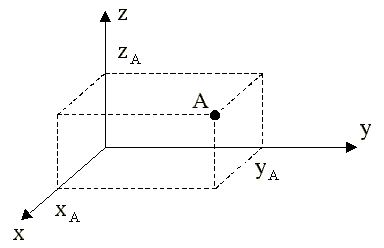
3.4.1. Координаты точки
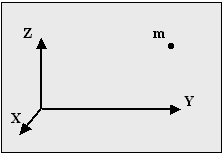
Первый способ задать положение материальной точки - это задать ее координаты. Например, три числа xА, yА, zА задают положение точки A в декартовой системе координат.
3.4.2. Радиус-вектор r - это вектор, проведенный из начала координат (3.3) в какую-либо точку пространства.
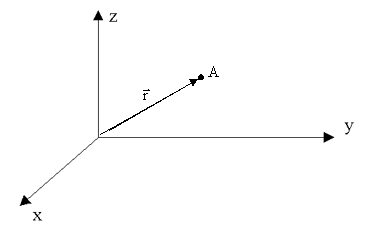
3.4.2.1. Компоненты радиус-вектора
На плоскости:
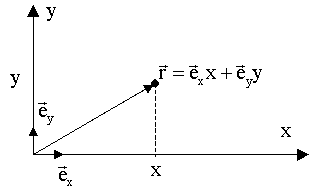
В трехмерном пространстве:
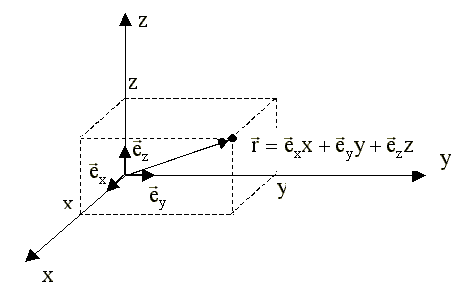
-
![]() -
единичные векторы или орты, направленные
по осям x, y, z соответственно;
-
единичные векторы или орты, направленные
по осям x, y, z соответственно;
- x, y, z - компоненты радиуса - вектора. Очевидно, они же являются координатами материальной точки.
3.4.2.2. Модуль радиус-вектора
![]() - по теореме
Пифагора.
- по теореме
Пифагора.
3.5. Траектория - это линия, описываемая материальной точкой при ее движении.
3.6. Путь - длина отрезка траектории (3.5) .
3.7. Перемещение - вектор, проведенный из начального положения (3.4.1), (3.4.2) материальной точки (3.1.1) в ее конечное положение.
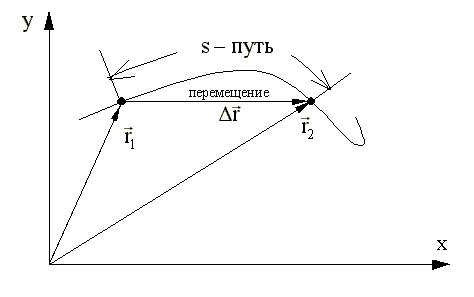
3.8. Скорость - это производная радиуса - вектора по времени.
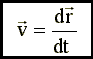 либо,
применяя другое обозначение производной
по времени,
либо,
применяя другое обозначение производной
по времени,
![]()