3. Параметрические и непараметрические показатели тесноты связей, основные направления их применения.

Теснота (сила) корреляционной зависимости измеряется при помощи коэффициента корреляции, который определяется по формуле:

• при парной корреляции:

• при множественной корреляции для двух факторов:

Линейный коэффициент корреляции изменяется от –1 до +1, чем ближе его значение к единице, тем теснее связь между изучаемыми признаками, и, наоборот, с приближением значения коэффициента корреляции к нулю связь становится менее существенной. Если:

– связь между факторами очень слабая;

– заметная;

– существенная;

– тесная;

– очень тесная.

По направлению выделяют связь прямую и обратную.

При прямой связи с увеличением значений факторного признака происходит увеличение значений результативного признака, а при обратной связи с увеличением значений факторного признака происходит уменьшение значений результативного. Знаки коэффициентов регрессии и корреляции совпадают.

При этом интерпретацию выходных значений коэффициента корреляции можно представить в следующей таблице.

Оценка линейного коэффициента корреляции

Значение коэффициента корреляции	Характер связи	Интерпретация связи
	отсутствует	–
	прямая	с увеличением Х увеличивается У
	обратная	с увеличением Х уменьшается У, и наоборот
	функциональная	каждому значению факторного признака строго соответствует одно значение результативного признака

После определения тесноты связи вычисляется коэффициент детерминации:

Коэффициент детерминации показывает, на сколько процентов изменения в уровне результативного признака обусловлены влиянием факторных признаков.

Тема 10. Статистика населения.

Цель: развить у студентов способность к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения, научиться выбирать инструментальные средства для обработки экономических данных статистики населения в соответствии с поставленной задачей, анализировать результаты расчетов и обосновывать полученные выводы.

Отрабатываемые вопросы:

1. Население как субъект и объект экономической деятельности.

2. Категории постоянного и наличного населения, связь между ними.

3. Показатели оценки демографической ситуации территории.

4. Оценка численности населения, показатели средней численности населения, методы их исчисления.

1. Население как субъект и объект экономической деятельности.

Статистика населения – древнейшая отрасль статистической науки, которая изучает население и процессы, связанные с его динамикой, с количественной стороны в конкретных условиях общественного развития. Таким образом, предметом изучения этой отрасли статистики являются население и закономерности его развития.

Население – это совокупность людей, проживающих в пределах определенной территории: части страны, всей страны, группы стран, всего земного шара. К числу демографических процессов относятся:

а) процессы естественного движения населения и смены поколений, т.е. воспроизводства;

б) процессы изменения структуры населения (по полу, возрасту, социальному и экономическому составу, уровню образования и грамотности, этническим группам);

в) процессы изменения размещения населения по территории;

г) процессы миграции населения.

Как известно, свой предмет статистика изучает при помощи совокупности специфических приемов и способов, составляющих ее метод. Наряду с общепринятыми приемами массового наблюдения, сводки и группировки его данных, обобщающих показателей, статистика населения использует свои, особенные способы, такие как построение вероятностных таблиц, демографической сетки, возрастных пирамид и др.

Основная цель расчета показателей статистики населения – оценка демографической ситуации, сложившейся на конкретной территории в конкретных условиях места и времени, ее прогноз на будущее. В состав системы показателей оценки демографической ситуации включаются показатели:

а) динамики численности населения;

б) его естественного движения;

в) миграции;

г) размещения населения;

д) состава и структуры населения;

е) продолжительности жизни и воспроизводства населения.

Расчет демографических показателей очень часто бывает, связан с необходимостью определения среднегодовой численности населения территории. Выбор способа ее расчета зависит от исходных данных.

Если имеются данные на начало (S₁) и конец периода (S₂), то средняя численность населения определяется по формуле средней арифметической простой:

Если имеются данные равноотстоящего моментного ряда динамики, то:

где S₁, S₂, ..., S_n-1, S_n – численность населения на начало месяца;

n – число месяцев.

Если требуется найти среднюю численность населения в не равноотстоящем моментном ряду динамики, то используется формула средней арифметической взвешенной:

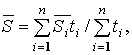
где – средняя численность населения в i-м интервале, рассчитываемая по приведенным выше формулам;

t_i – длительность i-го интервала времени. Если нужно определить среднюю численность населения за длительный период времени, то используется формула средней логарифмической:

где S₁ – численность населения на начало периода;

S_n – то же на конец периода.