1.6.Основные методы расчета электрических цепей

Метод узловых потенциалов позволяет уменьшить количество независимых уравнений системы до числа, равного количеству узлов без одного:

При составлении уравнений по методу узловых потенциалов (напряжений) вначале полагают равным нулю потенциал какого-либо узла (его называют базисным). Для определения потенциалов (напряжений) оставшихся узлов составляется следующая система уравнений:

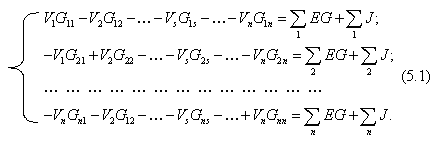
Здесь G_kk— сумма проводимостей всех ветвей, подсоединенных к узлу k (собственная проводимость узла k); G_km — сумма проводимостей всех ветвей, непосредственно соединяющих узел k с узлом m (взаимная проводимость узлов k и m ); — алгебраическая сумма произведений ЭДС ветвей, подсоединенных к узлу k, на проводимости этих ветвей ( со знаком плюс берутся ЭДС, которые направлены к узлу k , и со знаком минус — от узла k); — алгебраическая сумма токов источников тока, подсоединенных к узлу k (со знаком плюс берутся токи, которые направлены к узлу k, а со знаком минус — от узла k).

Путем решения системы уравнений (5.1) определяют потенциалы всех узлов схемы, а токи ветвей, соединяющих узлы, находят с помощью закона Ома для участка цепи.

Если в схеме некоторые узлы соединяются идеальными источниками ЭДС, то число уравнений, составляемых по методу узловых потенциалов, уменьшается.

Для схем, имеющих два узла (для определенности узлы a и b), узловое напряжение определяется формулой

, (5.2)

где — алгебраическая сумма произведений ЭДС ветвей на проводимости этих ветвей (ЭДС считаются положительными, если они направлены к узлу а, и отрицательными, если направлены от узла a); — алгебраическая сумма токов источников тока (токи положительны, если они направлены к узлу a , и отрицательны, если направлены от узла a); — сумма проводимостей всех ветвей, соединяющих узлы a и b.

Метод контурных токов основан на введении условных контурных токов, протекающих в каждом контуре цепи (по любой ветви цепи должен проходить хотя бы один выбранный контурный ток). При этом ток в любой ветви цепи можно представить в виде алгебраической суммы контурных токов, протекающих по этой ветви. Метод контурных токов позволяет уменьшить количество уравнений системы до числа K, равного общему числу неизвестных контурных токов, которое равно , где N_В – число ветвей цепи, N_у - число узлов цепи, N_Т – число ветвей цепи, содержащих идеальные источники тока. Рекомендуется выбирать контурных токов так, чтобы каждый из них проходил через один источник тока (эти контурные токи совпадают с соответствующими токами источников тока и они обычно являются заданными условиями задачи), а оставшиеся контурные токи выбирать проходящими по ветвям, не содержащим идеальных источников тока. Для определения последних контурных токов по второму закону Кирхгофа для этих контуров составляют K уравнений в виде

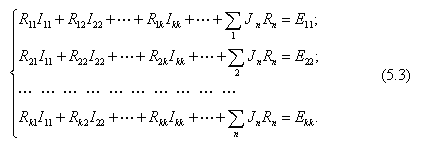
где — собственное сопротивление контура n (сумма сопротивлений всех ветвей, входящих в контур n); — общее сопротивление контуров n и l, причем = : если направления контурных токов в общей ветви для контуров n и l совпадают, то положительно ( > 0), в противном случае отрицательно ( _/< 0);

— алгебраическая сумма ЭДС, входящих в контур n; — общее сопротивление ветви контура n с контуром, содержащим источник тока : если направления контурных токов и токов источников в общей ветви совпадают, то положительно ( > 0), в противном случае отрицательно ( < 0);