Основные понятия, определения, законы электрических цепей.

Электрической цепью называют совокупность устройств, предназначенных для прохождения электрического тока, электромагнитные процессы в которых описываются с помощью понятий напряжения и тока. Электрорадиоэлементом (элементом) называют часть электрической цепи (ЭЦ), которая реализует некоторую элементарную функцию. Это источники (генераторы) электрической энергии, резисторы, конденсаторы и др.

По типу оператора ЭЦ делятся на линейные, когда их реакция на внешнее воздействие описывается линейным оператором и нелинейные, когда преобразование нелинейно. Далее будем рассматривать линейные ЭЦ.

Активные линейные элементы — источники электрической энергии.

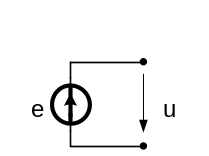
Идеальный независимый источник напряжения (ЭДС) (рис.1.2.а) характеризуется задающим напряжением u или электродвижущей силой (ЭДС) e. Напряжение на зажимах идеального источника напряжения (ЭДС) не зависит от величины протекающего через него тока, что показано на рис. 1.1.а) горизонтальной линией. Идеальный источник напряжения (ЭДС) имеет внутреннее сопротивление равное нулю.

Зависимость напряжения на зажимах элемента цепи от тока, протекающего через него, носит название вольт-амперной характеристики (ВАХ) данного элемента. ВАХ идеального источника напряжения (ЭДС) представляет собой прямую, параллельную оси тока (рис.1.1.а).

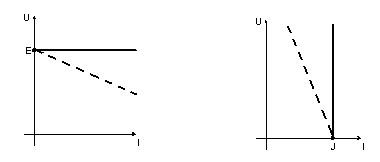
а) б)

Рис. 1.1

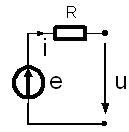
Реальный источник напряжения (ЭДС) (рис.1.2.б) с конечным внутренним сопротивлением может быть изображен в виде, последовательно соединенных идеального источника напряжения и внутреннего сопротивления R.

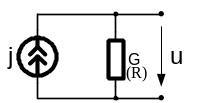
Идеальный независимый источник тока (рис.1.2.в) характеризуется своим задающим током j , величина которого не зависит от напряжения на зажимах источника. Внутренняя проводимость идеального источника тока равна нулю. ВАХ представляет собой прямую, параллельную оси напряжения (рис.1.1.б)).Реальный источник тока (рис.1.2.г) с конечной внутренней проводимостью может быть изображен в виде идеального источника тока и внутренней проводимости G, которые соединены параллельно. Напряжение на зажимах реальных источников тока и отдаваемый ими во внешнюю цепь ток зависят от параметров цепи. ВАХ реальных источников напряжения или тока имеет угол наклона, тангенс которого пропорционален внутреннему сопротивлению R или проводимости G соответственно. ВАХ реальных источников показаны на рис. 1.1 пунктирной линией для некоторого значения внутреннего сопротивления или проводимости, соответственно.

Переход от схемы источника напряжения к эквивалентной схеме источника тока осуществляется по формулам

(1.1)

a)

б)

в)

г)

Рис. 1.2

1. Пассивные линейные элементы.

Резистивное сопротивление или сопротивление (обозначается R) — идеализированный элемент, обладающий свойством необратимого рассеивания энергии.

Ток и напряжение на резистивном сопротивлении определяются законом Ома

, (1.2)

где R-сопротивление,Ом G - электрическая проводимость,См

(1.3)

Индуктивный элемент или индуктивность (обозначается L),Гн — идеализированный элемент, обладающий свойством накапливать и отдавать энергию магнитного поля. Ток и напряжение на индуктивности связаны следующими соотношениями:

(1.4)

Емкостной элемент или емкость (обозначается С),Ф — идеализированный элемент, обладающий свойством накапливать и отдавать энергию электрического поля. Ток и напряжение на емкости связаны следующими соотношениями:

(1.5)

.

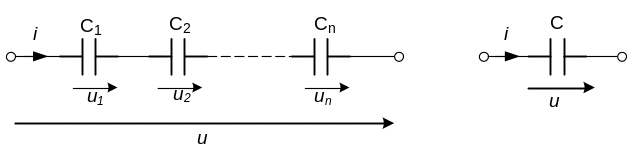
2. Топология электрических цепей

Для расчета ЭЦ используют их модели в виде электрических схем, на которых изображаются идеализированные элементы цепи.

Место (точка) соединения нескольких элементов на схеме называется узлом. Если узел образуется соединением только двух элементов, то он называется простым или устранимым. Такой узел на схеме не показывается. Если узел образуется соединением большего, чем два, числа элементов, то он называется сложным и изображается на схеме жирной точкой.

Часть схемы между двумя сложными узлами называется ветвью.

Ветви, подсоединенные к одной паре узлов, образуют параллельное соединение. На рис. 1.3 для примера изображена схема цепи постоянного тока, на которой стрелками показаны три контура.

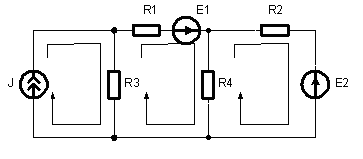
Рис. 1.3

Замкнутый участок цепи, образующий замкнутый путь называется контуром.

Двухполюсником называется электрическая цепь (или часть ЭЦ), имеющая два зажима (вывода, полюса) для подключения к внешней цепи (остальной части ЭЦ).

Двухполюсник называется активным, если он содержит хотя бы один источник электрической энергии и напряжение холостого хода на его зажимах не равно нулю, и пассивным в противном случае. Двухполюсники, обладающие одинаковыми входными характеристиками, называются эквивалентными.

Анализ цепей при постоянном воздействии

3. Закон Ома

Закон Ома применяется для отдельной ветви или для одноконтурной замкнутой цепи (не имеющей разветвлений).

При расчете тока по закону Ома прежде всего необходимо задать произвольно положительное направление тока.

Для ветви между узлами a,b при положительном направлении тока от узла a к узлу b

, (1.6)

где и — потенциалы узлов a и b; = — — разность потенциалов или напряжение между узлами a и b; — алгебраическая сумма ЭДС, находящихся в этой ветви (ЭДС, совпадающая по направлению с током, учитывается со знаком «+», направленная встречно – «-»); — арифметическая сумма сопротивлений ветви (полное сопротивление ветви между узлами a и b).

Формулу (1.6) называют обобщенным законом Ома.

Для замкнутой одноконтурной цепи

(1.7)

где — арифметическая сумма всех сопротивлений цепи; — алгебраическая сумма электродвижущих сил в цепи.

Со знаком плюс учитываются те ЭДС, направления которых совпадают с выбранным положительным направлением тока, а со знаком минус — ЭДС с противоположными направлениями.

Пример анализа цепи по закону Ома. Для цепи, приведенной на рисунке 2.1, рассчитать токи в ветвях с резистивными сопротивлениями, используя закон Ома.

E₁ = E₂ = 10 B E₃ = 20 B R₁ = R₂ = R₃ = 10 Ом

Рис. 2.1

Цепь содержит два узла и три ветви. Обозначим токи ветвей и зададим их положительные направления.

Идеальный источник ЭДС E3 задает напряжение между узлами a и b. Учитывая, что стрелка ЭДС направлена в сторону большего потенциала (т.е. к «+ »), получаем: U_ab = E₃

Теперь по закону Ома рассчитываем токи в ветвях с резистивными сопротивлениями.

I₁ = = 2 A I₂ = = - 0,5 A

Значение второго тока получилось отрицательным, следовательно, действительное направление данного тока противоположно направлению, выбранному нами. Ток в ветви с источником E₃ рассчитать по закону Ома не возможно, т.к. сопротивление ветви равно нулю. Он может быть рассчитан по закону Кирхгофа.