Обратная кристаллическая решетка, сфера Эвальда и структурные факторы

Напомним, что структуру макромолекулы можно рассчитать с помощью преобразования Фурье ее дифракционных волн:

В случае кристалла f(q) заменяется на g(q), где

Следуя правилу кристаллографии, мы заменяем Q на S, где Q =2πS. Напомним, что S = 2 sinθ/λ, и что максимумы встречаются только для значений S, заданных индексами hkl:

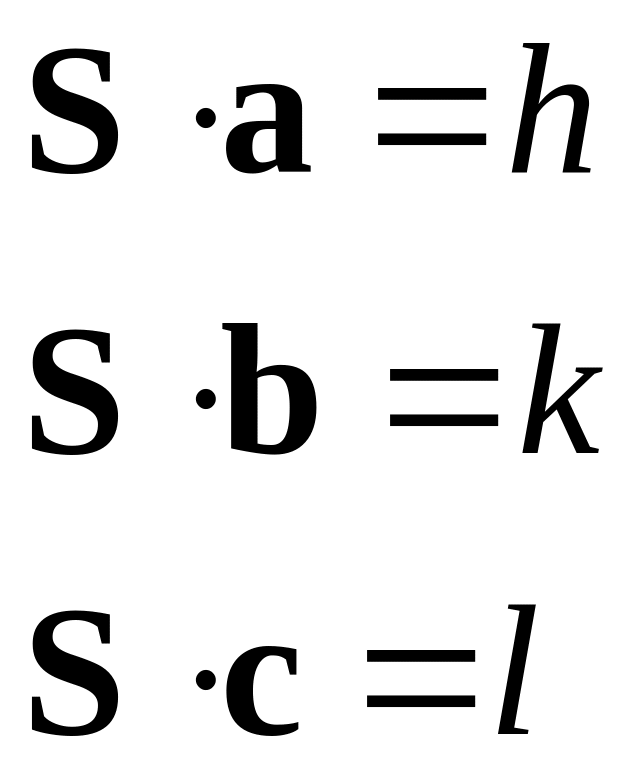
По аналогии с одномерной обратной кристаллической решеткой, S определяет обратную кристаллическую решетку в трех измерениях. Сфера Эвальда с радиусом 1/λ центрируется в кристалле. Каждый узел обратной кристаллической решетки имеет координаты hkl. Условие, при котором некоторый луч CP представляет собой дифрагированный луч, выражается так: дифрагированный рентгеновский луч будет иметь направление SP, если точка P представляет собой узел обратной решетки (h, k, l), т. е. вектор ОP есть вектор обратной решетки (Рис. Е3.1). Следовательно, чтобы некоторое отражение hkl соответствовало условию дифракции, кристалл следует повернуть таким образом, чтобы этот узел обратной решетки попал на сферу отражения дифракции.

Рис. Е3.1 Диаграмма Эвальда: условия дифракции выполняются в точке Р. Угол OSP = 2θ

Закон Брэгга.

Полезно представить кристалл как набор повторяющихся граней в пространстве. Конструктивная интерференция происходит только при определенных углах, определяемых брэгговским законом:

nλ = 2d sin θ,

где n – целое число, λ – длина волны, d – расстояние между повторяющимися плоскостями в кристалле, а θ – угол падения излучения.

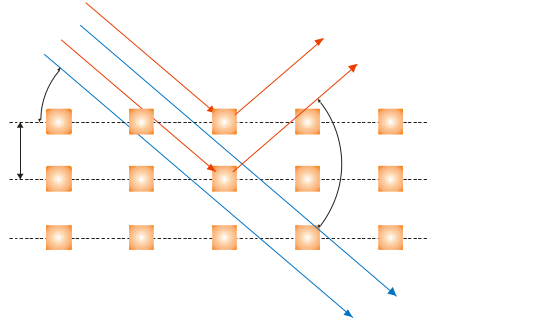
Дифракционная картина, обусловленная атомами лишь в одной элементарной ячейке, не будет содержать дискретных максимумов, так как нет никакой периодичности в ее пределах, и мы получим лишь непрерывное распределение интенсивности. Наличие множества элементарных ячеек в кристалле и их трехмерная периодичность приводят к тому, что бóльшая часть излучения, рассеиваемого одной элементарной ячейкой, гасится и остаются лишь волны, удовлетворяющие условию Брэгга.

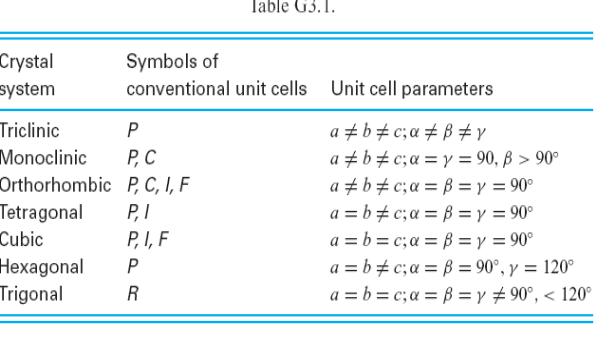
Таблица Е3.1.

Кристаллическая система	Обозначения общепринятых элементарных ячеек	Параметры элементарных ячеек
Триклинная
Моноклинная
Орторомбическая
Тетрагональная
Кубическая
Гексагональная
Тригональная

Для описания пространственных групп была разработана система условных обозначений, в которой буква и ряд цифр соответствуют определенным математическим действиям. Буква относится к типу кристаллической решетки. Например, P обозначает примитивную решетку (узлы расположены только по углам элементарной ячейки), F – гранецентрированную решетку (дополнительные узлы – на гранях элементарной ячейки) и I – объемно-центрированную решетку (добавочный узел находится в центре элементарной ячейки). Большие цифры обозначают симметрию относительно осей a, b и c пространственной группы соответственно, в то время как цифры нижних индексов указывают на наличие винтовой оси симметрии.