Разрешающая способность и контраст

Биологические макромолекулы и структуры обычно находятся в водной среде. Это очевидно для растворов белков. Однако кристаллы белков, волокна ДНК, образцы мембран также содержат значительные объёмы растворяющей жидкости. Опыт дифракции на чётко организованном (когерентном) образце должен предоставить информацию о положении всех атомов, независимо от того, находятся ли они в растворяющей жидкости или макромолекулах. Однако на практике разрешающая способность может быть ограничена размерами величины объёма многих атомов. Это особенно относится к разупорядоченным областям раствора. В таких случаях полезно определить плотность рассеивания, т.е. амплитуду рассеивания на единицу объёма.

Разрешающая способность и однородность растворяющего вещества

Ясно, что вода не однородна при разрешении выше 3 Å. При 10 Å (максимум Q ~ 0.6 Å⁻¹), она может считаться однородной, с постоянной плотностью рассеивания, ρ◦ = (f )/V, где V объём, содержащий атомы с общей амплитудой рассеивания f. Расчётный объём молекулы воды в жидкости 30 ų, при плотности 1 гсм^-3. Так как в молекуле H₂O содержится 10 электронов, ρ◦ = 0.33 электронов Å⁻³ для рентгеновских лучей. Соответствующая амплитуда для нейтронов 0.56 фм Å⁻³.

Понятие контраста между двумя частями образца относится к разнице между их плотностями рассеивания.

Результирующую волну, рассеянную системой атомов в направлении, соответствующем заданному вектору рассеивания можно представить как

F(Q) =_jfj exp(iQ· rj)

Теперь рассмотрим одну макромолекулу в растворе, схематически показанную на рис. Е1.12. Для того, чтобы рассчитать, как система рассеивает излучение, сумма в уравнении должна быть больше всех атомов в растворе, атомов в макромолекуле и атомов в растворяющей жидкости. Частица полностью описана амплитудами рассеивания f_j в положениях r_j её атомов, и она окружена бесконечным однородным раствором с плотностью рассеивания ρ◦.

Рис. Е1.12. Частица в растворе.

Частица представлена как "рыбка", чтобы подчеркнуть, что биологические макромолекулы складываются и достигают четвертичных структур посредством реакции с водным раствором.

Теперь мы разделим систему рассеивания на макромолекулу с одной стороны и растворяющую жидкость с другой (Рис. Е1.13). Первая часть, (a), это частица (включая возмущённое растворяющее вещество). Вторая часть, (б), это однородное бесконечное растворяющее вещество.

Однако учтите, что сумма (a) и (б) включает в себя дополнительный объём растворяющего вещества, (в), если сравнивать с исходной системой рассеивания – объём, соответствующий забранному частицей. Поэтому частица в системе рассеивающего раствора равна a + b -- c, что аналогично закону Архимеда для плавучести частицы в жидкости. Сумма волн от каждой части приведена на правой стороне рис. Е1.13. Волны от однородного растворяющего вещества появляются в очень узком диапазоне, близком при Q = 0, так что (б) на практике не соблюдается.

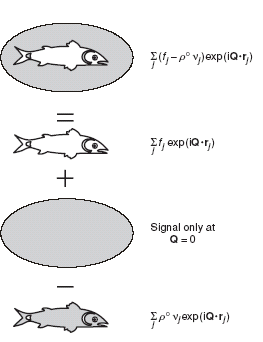
Рис. Е1.13 Рассеивание от частицы в растворе.

Таким образом, амплитуда рассеивания от частицы в растворе представлена следующим выражением

(Е1.16)

где v_j объём атома j. Выражение f j − ρ◦v_j является амплитудой контраста атома j относительно растворяющего вещества. Средняя амплитуда контраста частицы представляется выражением (∑(f_j − ρ◦v_j) или ∑f_j − ρ◦V, где V является общим объёмом частицы. Средний контраст плотности рассеивания частицы равен ρ - ρ◦, где ρ =∑(f_j) / V.

Учёт контраста действителен для опытов с малым углом рассеивания в растворе, и кристаллографии (дифракция волокон и мембран) только при малом разрешении.

Методика рентгеновской и нейтронной дифракции