Двумерные и трёхмерные кристаллы

Теперь понятно как расширить уравнение (Е1.13) до двумерных (как в случае мембран с плоскостной организацией) и трёхмерных кристаллов, используя соответствующие векторы R и Q.

Для трёхмерного кристалла R = a + b + c, где a, b, c являются векторами вдоль трёх осей (Рис. Е1.9). Заменяя R в уравнении (Е1.13), получаем

(Е1.14)

где t, u, и v являются целыми числами.

Аналогично для одномерного случая, если кристалл содержит очень большое количество элементарных ячеек, все фазы, за исключением соответствующих позициям дифракции пространственной решётки, производят деструктивную интерференцию, так что дифракция наблюдается только при

Q·a = 2π h Q·b = 2π k Q·с = 2πl (Е1.15)

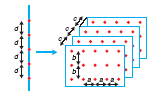
Рис. Е.1.9 Принципиальная схема одно- и трёхмерных кристаллов. Красные точки представляют начальные точки рассеянных волн. В одномерной пространственной решётке начальные точки отстоят друг от друга на расстоянии d, а в трёхмерной решётке начальные точки отстоят на расстояния a, b, и c вдоль соответствующих осей.

Обычно в кристаллографии используется вектор рассеяния S вместо Q, где Q = 2π.S. Тогда уравнение Е1.15 примет вид

S·a = h S·b = k S·c = l

h, k и l являются целыми числами и обычно описывают дифракционный максимум своими индексами (h, k, l); их называют индексами Миллера (Рис. Е1.10).

В итоге дифракционная диаграмма направленности от кристалла содержит два уровня информации: пространственное расположение элементарных ячеек может быть установлено по равномерному расстоянию максимальной дифракционной диаграммы направленности (обозначенной индексами hkl); амплитуды дифракционных диаграмм направленности содержат информацию по организации атомов в каждой элементарной ячейке. Дифракция рентгеновских лучей в кристалле может быть представлена как зеркальное отражение по закону Брэгга всех плоскостей, которые можно представить в кристаллической решетке.

Рис. Е.1.10. Пример шести наборов плоскостей, характеризующимися разными Миллеровскими индексами. Разделение ребер кристаллической решетки на некоторое число частей, соответствующих реальным расстояниям между ее элементами, однозначно определяет ориентацию любой плоскости.

Разупорядоченные системы

Конструкцию на рис. Е1.8 достаточно часто можно использовать не только в случае нормально организованных пространственных решёток. На рис. Е1.11 показан пример концентрированного раствора (одномерный для простоты, но аргументация сохраняется для трёхмерного).

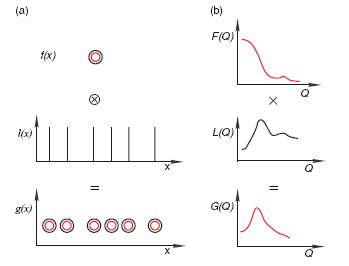
Рис. Е1.11. (a) Реальное пространство: жидкость из больших частиц рассматривается как свёртка одной частицы с разупорядоченной пространственной решёткой функций Дирака. (б) Соответствующие преобразования Фурье в обратном пространстве.

Учтите, что L(Q), преобразование Фурье для разупорядоченной пространственной решётки, является непрерывной функцией с размытым максимумом, соответствующим наиболее частому расстоянию между частицами в жидкости. G(Q)=F(Q)L(Q) также непрерывная функция. Однако, пик G(Q) получается из внутренней структуры частицы и её промежутка в растворе.