Теория поляризации для разбавленных растворов, находящихся в стеклообразном состоянии

Анизотропия флуоресценции, измеряемая в разбавленных стеклообразных растворах, определяется собственными спектральными свойствами флуорофоров. Это происходит потому, что высокая вязкость раствора препятствует заметной вращательной диффузии до испускания. Более того, в очень разбавленных растворах ни перенос энергии, ни реабсорбция не могут вызвать деполяризацию испускания. Этот особый случай будет описан детально потому, что его обсуждение без чрезмерного усложнения выявляет фундаментальные свойства анизотропии.

Теория поляризации флуоресценции основывается на рассмотрении флуорофора как осциллирующего диполя, имеющего момент

где ω_L – круговая частота испускаемого света; t – время. Естественно, флуорофор испускает отдельные фотоны. Однако пространственная зависимость энергии точно описывается классическими (не квантовыми) теория­ми электричества и магнетизма. Предположим, что данный флуорофор ориентирован вдоль оси z, как показано на рис. 5.2. Пространственное распределение энергии, излучаемой осциллирующим диполем, идентично распределению излучения антенны, которая также является осциллирующим диполем. Электрическое поле А такого диполя на определенном расстоянии пропорционально sin ψ где ψ – угол по отношению к оси z:

Испускаемая энергия и, следовательно, наблюдаемая интенсивность I пропорциональны квадрату интенсивности электрического поля. Следовательно,

Применительно к поляризации флуоресценции наиболее важной характеристикой излучаемого света является его круговое симметричное распределение вдоль оси z. Для диполя, ориентированного вдоль оси z, следует ожидать одинаковой интенсивности света в направлениях у и х. Интересно отметить, что в направлении оси z нельзя наблюдать этот осциллирующий диполь, так как вдоль этого направления энергия не излучается. Мы будем говорить о моментах переходов при возбуждении и испускании как о поглощающих и испускающих диполях.

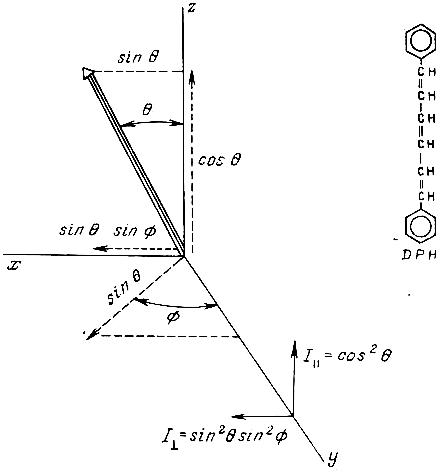
РИС. 5.3. Система координат для флуорофора.

Рассмотрим флуорофор, диполи поглощения и испускания которого параллельны. Это практически верно для 1,6-дифенилгексатриена (рис. 5.3), который широко используется как зонд при изучении биологических мембран. В данный момент примем, что эта молекула ориентирована под углом в по отношению к оси z и ф – по отношению к оси у. Естественно, молекулы DPH будут случайным образом ориентированы в изотропном и гомогенном стеклообразном растворителе, и возбуждение поляризованным светом отбирает определенный диапазон ориентации (разд. 5.2.1). Пусть нужно вычислить анизотропию, которая наблюдалась бы для этой молекулы в стеклообразном растворе. Предварительное условие параллельности диполей, неподвижность и случайный характер ориентации упрощают вывод. Тем не менее рассмотрение этого простого случая иллюстрирует смысл измеряемого значения анизотропии.

Интенсивность света, излученного диполем, пропорциональна квадрату проекции его вектора на ось наблюдения. Следовательно,

( 5.10), (5.11)

В реальных экспериментах возбуждение будет направлено вдоль оси х. При этом с одинаковой вероятностью должны возбудиться все молекулы, имеющие равные углы 9, т.е. популяция возбужденных флуорофоров будет симметрично распределена вокруг оси z, Любая экспериментально доступная популяция молекул будет ориентирована так, что угол ф будет принимать значения от 0 до 2 π с равной вероятностью. Следовательно, мы можем исключить зависимость от φ в уравнении (5.11). Среднее значение sin²φ опре­деляется выражением

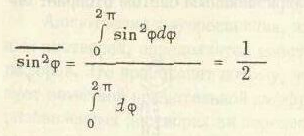
(5.12)

и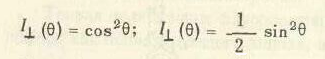 , следовательно,

(5.13),(5.14)

Теперь предположим, что наблюдаем набор флуррофоров, которые ориентированы по отношению к оси z с вероятностью f(θ). В следующем разделе будет рассмотрен вид f(θ), предполагаемый для случайного распределения. Измеряемые интенсивности флуоресценции для этого набора молекул равны:

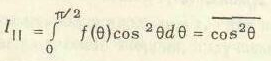
(5.15)

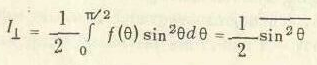
(5.16)

где f(θ)dθ — вероятность того, что флуорофор ориентирован между θ и θ + dθ. Используя уравнение (5.2) и равенство sin²θ = 1 — cos^aθ, можно показать, что

( 5.17)

Следовательно, величина анизотропии на самом деле является мерой среднего значения cos ²θ, где θ — угол диполя испускания по отношению к оси z. Это происходит потому, что наблюдаемые интенсивности I_|| и I_┴ пропорциональны квадрату проекций индивидуальных моментов перехода на оси х и z (см. рис. 5.2). Полезно рассмотреть взаимосвязь между r и θ. Рассеянный свет полностью поляризован, следовательно, θ = 0 и r =1,0. Полное исчез­новение анизотропии эквивалентно θ = 54,7°. Это не означает, что каждый флуорофор поворачивается на 54,7°, но среднее значение cos²θ =1/3, где θ – угловое смещение между диполями возбуждения и испускания. Напомним, чт( при выводе уравнения (5.17) предполагалось, что эти диполи параллельны. Не сколько более сложное выражение необходимо практически для всех флуорофоров, поскольку диполи редко бывают параллельны. К тому же мы еще не рассмотрели влияние фотоотбора на величину анизотропии.

ВОЗБУЖДЕНИЕ И ФОТООТБОР ФЛУОРОФОРОВ. Для наблюдения флуорес­ценции флуорофоры, разумеется, необходимо возбудить. Электрический диполь флуорофора не обязательно должен точно совпадать с направлением оси z для поглощения света, поляризованного вдоль этой оси. Вероятность поглощения пропорциональна cos² θ, где θ — угол, образуемый диполем поглощения с осью z [3]. Следовательно, возбуждение поляризованным светом приводит к появлению популяции возбужденных флуорофоров, которая симметрично распределена вокруг оси z (рис. 5.4).

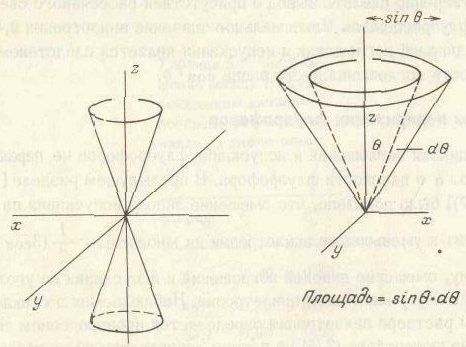
РИС. 5.4. Схемы, иллюстрирующие фотоотбор и вероятность распределения флуорофоров.

Это явление называется фотоотбором. Распределение cos²θ видоизменяется в дальнейшем путем учета вероятности того, что молекула образует угол θ с осью z. Для случайного распределения, которое должно существовать в неупорядоченном растворе, число молекул с величиной угла между 6 и 9 + dθ пропорционально sinθdθ, a также площади поверхности на сфере внутри угла от θ до θ + dθ. Следовательно, распределение возбужденных вертикально поляризованным све­том молекул выражается как

( 5.18)

Распределение вероятности, даваемое уравнением (5.18), определяет мак­симум отбора, который может быть достигнут при использовании оптического возбуждения изотропного раствора. Напомним [уравнение (5.17)], что анизотропия является просто линейной функцией cos²θ. Следовательно, для однонаправленных диполей поглощения и испускания максимальные значения cos²θ даются выражением

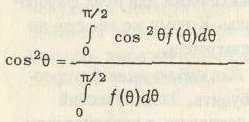(5.19)

Подстановка (5.18) в (5.19) дает cos²θ = 3/5. С учетом уравнения (5.17) мож­но найти максимальную анизотропию, равную 0,4, Это значение получается, когда диполи поглощения и испускания параллельны и нет других процессов, приводящих к деполяризации. Легко заметить, что это значение (0,4) гораздо меньше, чем возможное для рассеянного света (1,0). Фактически, если измеренная анизотропия для случайно ориентированного образца больше чем 0,4, можно уверенно сделать вывод о присутствии рассеянного света в до­полнение к флуоресценции. Максимальное значение анизотропии 0,4 для параллельных диполей поглощения и испускания является следствием того, что вероятность поглощения света равна cos ² θ.