Стационарное двойное лучепреломление. Закон Керра
Зависимость между оптической анизотропией и величиной электрического двойного лучепреломления раствора макромолекул выражается следующим соотношением:
(28.8)
где
– это объемная доля растворенных
макромолекул,
n
– показатель
преломления
раствора
в отсутствие электрического поля.
Двойное лучепреломление пропорционально
произведению
фактора оптической анизотропии, (g1
– g2),
на функцию распределения ориентации,
.
При долговременном действии электрического
поля функция распределения ориентации,
,
принимает вид:
(28.9)
где θ
– угол
между осью симметрии макромолекулы и
направлением поля, а
означает
усреднение по ансамблю.
Когда эффект ориентации, обусловленный электрическим полем, уравновешивается эффектом дeзориентации, обусловленным броуновским движением, то:
(28.10)
где α1 и α2 – избыточная электрическая поляризуемость вдоль оси симметрии и продольных осей, соответственно. Таким образом, двойное лучепреломление пропорционально квадрату силы поля в области малых полей. Это закон называется законом Керра. Уравнение 28.10 демонстрирует, что в DR-экспериментах молекулы имеют тенденцию ориентироваться в поле через взаимодействие индуцированных (α1 − α2), и/или постоянных, μ, диполей с приложенным электрическим полем.
Константа пропорциональности K называется константой Керра. Она равна:
K
=
(28.11)
Таким образом, константа Керра является произведением двух вкладов, один из которых оптической природы (g1 − g2), а второй электрической природы (μ2·k-2·T-2 + (α1 − α2)·k-1T-1). Поэтому определить индивидуальный вклад в константу Керра невозможно.
Процесс спада двойного лучепреломления
При выключении электрического поля будет происходить дезориентация макромолекул под действием броуновского движения, что приводит к спаду двойного лучепреломления. В этом случае из кривой спада можно прямо вычислить время релаксации молекулы τ, поскольку оно описывается формулой:
(28.12)
где Δn – значение величины двойного лучепреломления в любое время t после начала спада, а Δn0 – начальная величина двойного лучепреломления в момент время t = 0.
Вспомним, что
время релаксации τ
связано
с константой вращательной диффузии
.
Таким образом, анализ кривой спада
двойного лучепреломления обеспечивает
самый прямой и удобный способ определения
константы вращательной диффузии, по
сравнению с такими методами, как двойное
лучепреломление в потоке или деполяризация
флуоресценции.
Процесс нарастания двойного лучепреломления
При низких значениях величины поля зависимость двойного лучепреломления Δn от времени t описывается более сложным выражением:
(28.13)
где, Δn0 является значением Δn при t →∞ и эквивалентно постоянному значению, приведенному в уравнении (28.10). Параметр A является отношением вклада постоянного диполя к вкладу индуцированного диполя и для стационарного случая при низкой величине поля имеет вид:
(28.14)
Когда ориентация полностью обусловлена анизотропией электрической поляризуемости (т. e. A = 0), уравнение (28.13) сокращается до:
(28.15)
В этом случае нарастание и спад кривых симметричны. С другой стороны, когда ориентация обусловлена постоянным дипольным моментом (т.e. A = ∞), уравнение 28.13 трансформируется как:
(28.16)
В этом случае нарастание идет гораздо медленнее, чем спад и параметр A может быть вычислен из формы кривой нарастания.
Другой метод определения параметра A есть метод площадей (рис. 28.6).
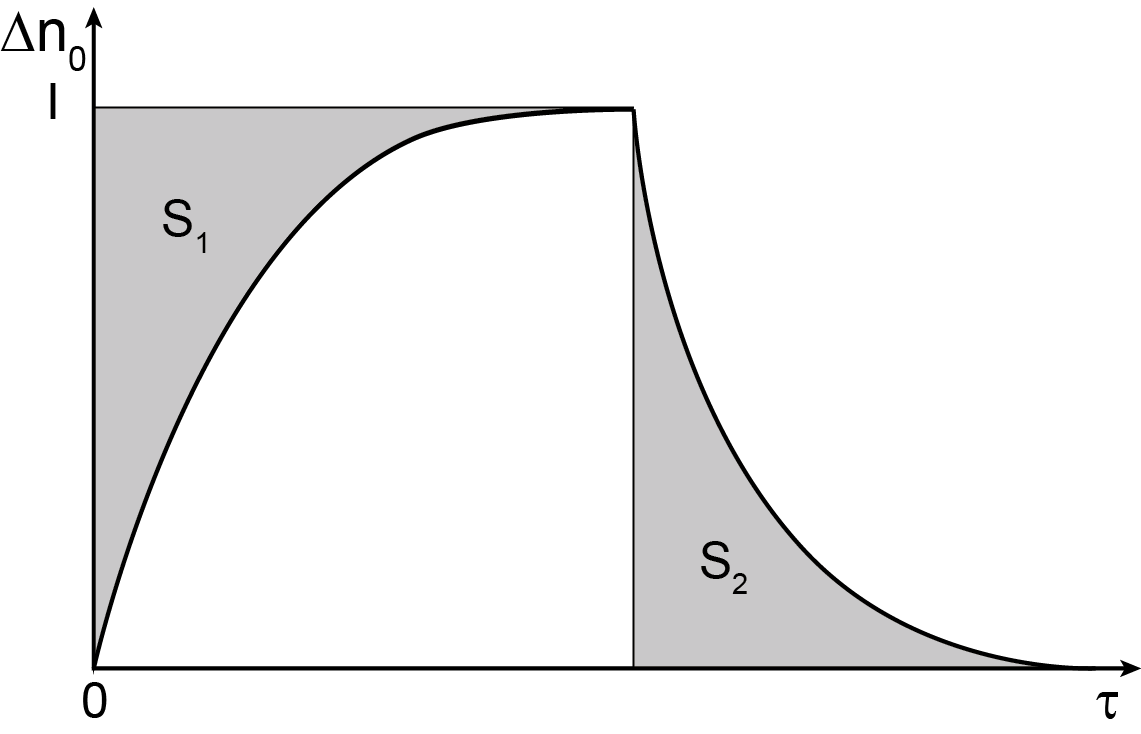
Рис. 28.6. Нормализованные кривые нарастания и спада Δn/ Δn0 в зависимости от времени (метод площадей)
Если площадь S1 – площадь под кривой нарастания, а S2 – площадь под кривой спада, то эти площади при низких полях связаны отношением:
(28.17)
Отметим, что отношение S1/S2 равно 1 для A = 0, и равно 4 для A=∞.