15 Лекция 5 лекция 5. Равновесная и скоростная седиментация Два типа экспериментов

В аналитическом ультрацентрифугировании имеются два комплементарных метода с различными экспериментальными протоколами, но с использованием одного и того же оборудования: скоростная седиментация и равновесная седиментация.

Таблица 25.1. Два типа экспериментов в аналитической ультрацентрифуге

Обсуждаемая характеристика	Скоростная седиментация	Равновесная седиментация
Угловая скорость	Большая (как правило); выбирается согласно седиментационным свойствам частицы	Небольшая (как правило); выбирается согласно седиментационным свойствам частицы
Тип анализа	Концентрация как функция времени и расстояния в течение нескольких часов	Концентрация как функция расстояния после достижения равновесия (24 часа и более)
Тип измерения	Наблюдение за движением границы	Наблюдение за распределением концентрации молекул в ячейке
Вычисляемые параметры	Размеры и конформация частиц	Молекулярная масса и полидисперсность
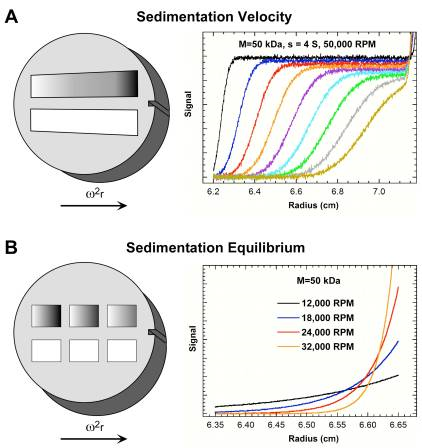
Типичные профили седиментации для глобулярного белка с молекулярной мас- сой 50 кДа (s = 4 S)
	Седиментационный профиль показан для одной скорости вращения в двухсекторной ячейке Сканы записаны через фиксиро- ванные интервалы времени (20 минут.	Седиментационный профиль показан для четырех скоростей вращения ротора в шестисекторной ячейке и для одновременной загрузке трех растворов разной концентрации.

В первом из них используется высокая скорость ротора и длинные ячейки с тем, чтобы получить максимальное разрешение, обеспечить информацию о размере и форме молекул, а также их взаимодействиях. При равновесной седиментации, напротив, используется низкая скорость ротора и короткие ячейки, с тем, чтобы свести к минимуму время, необходимое для установления равновесия и обеспечить информацию о молекулярной массе, константах ассоциации и стехиометрии. Начнем с молекулярной массы.

Молекулярная масса

Если долгое время центрифугировать раствор, содержащий макромолекулы разной молекулярной массы, то через некоторое время самые большие молекулы осядут на дно центрифужной кюветы, a макромолекулы средней или малой молекулярной массы распределятся недалеко от дна кюветы и их положение не будет меняться во времени. Такое центрифугирование называется равновесным, поскольку устанавливается равновесие между гравитационными и диффузионными силами.

В экспериментах по равновесной седиментации объем изначально однородного раствора макромолекул центрифугируется при низкой угловой скорости по сравнению со скоростью, которая необходима для проведения эксперимента по скоростной седиментации. Начавшемуся процессу седиментации противостоит процесс диффузии. После определенного периода времени достигается равновесие, в котором концентрация макромолекул повышается экспоненциально по направлению к дну кюветы, по тому же принципу, как и концентрация газов распределяется в атмосфере под действием в гравитационного поля Земли. Поэтому молекулярная масса осаждающихся молекул может быть вычислена по распределению их концентрации на разных длинах ячейки. Время, необходимое для достижения равновесия пропорционально квадрату длины столба раствора в радиальном направлении. Так, если раствор в столбе длиной 6 мм достигнет равновесия через 72 часа, то тот же раствор в 3 мм столбе ‒ за 24 часа.

Распределение макромолекул по концентрации между точками мениска a и точкой r подчиняется экспоненциальному закону:

C(r) =C(a) exp{ω²M(1 – ρ) (r² – a²)/2RT} (25.3)

где С(r) – зависимость концентрации макромолекул от расстояния от поверхности мениска (r),

C(a) – концентрация в точке мениска,

 – скорость вращения ротора,

М – молекулярный вес,

– парциальный удельный объем,

ρ – плотность растворителя,

R – газовая постоянная,

а – высота столба раствора.

Зависимость ln [C(r)] от r²/2 представлена на рисунке 25.1a для монодисперсного раствора, a на рисунке 25.1 б – для полидисперсного раствора.

?

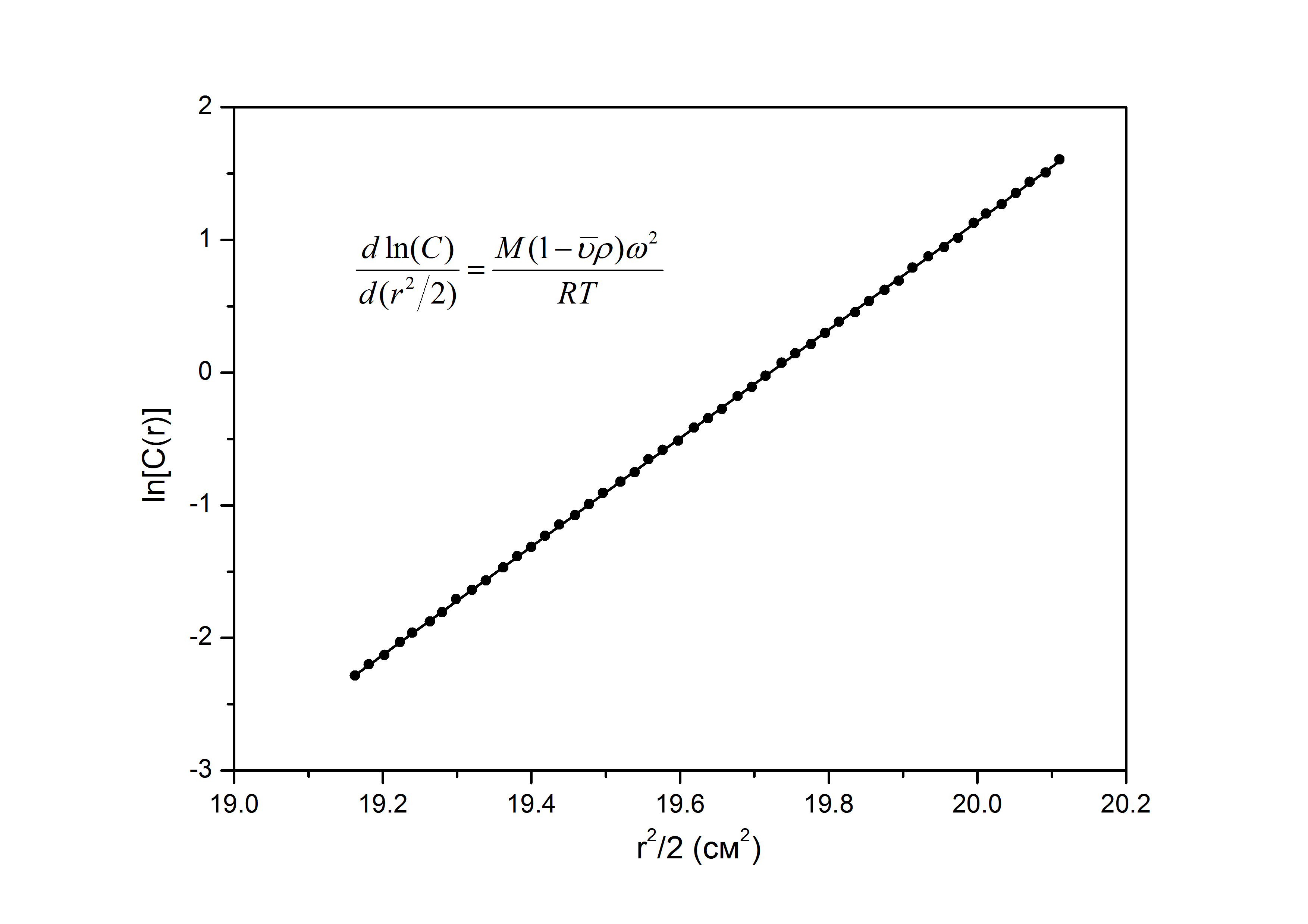
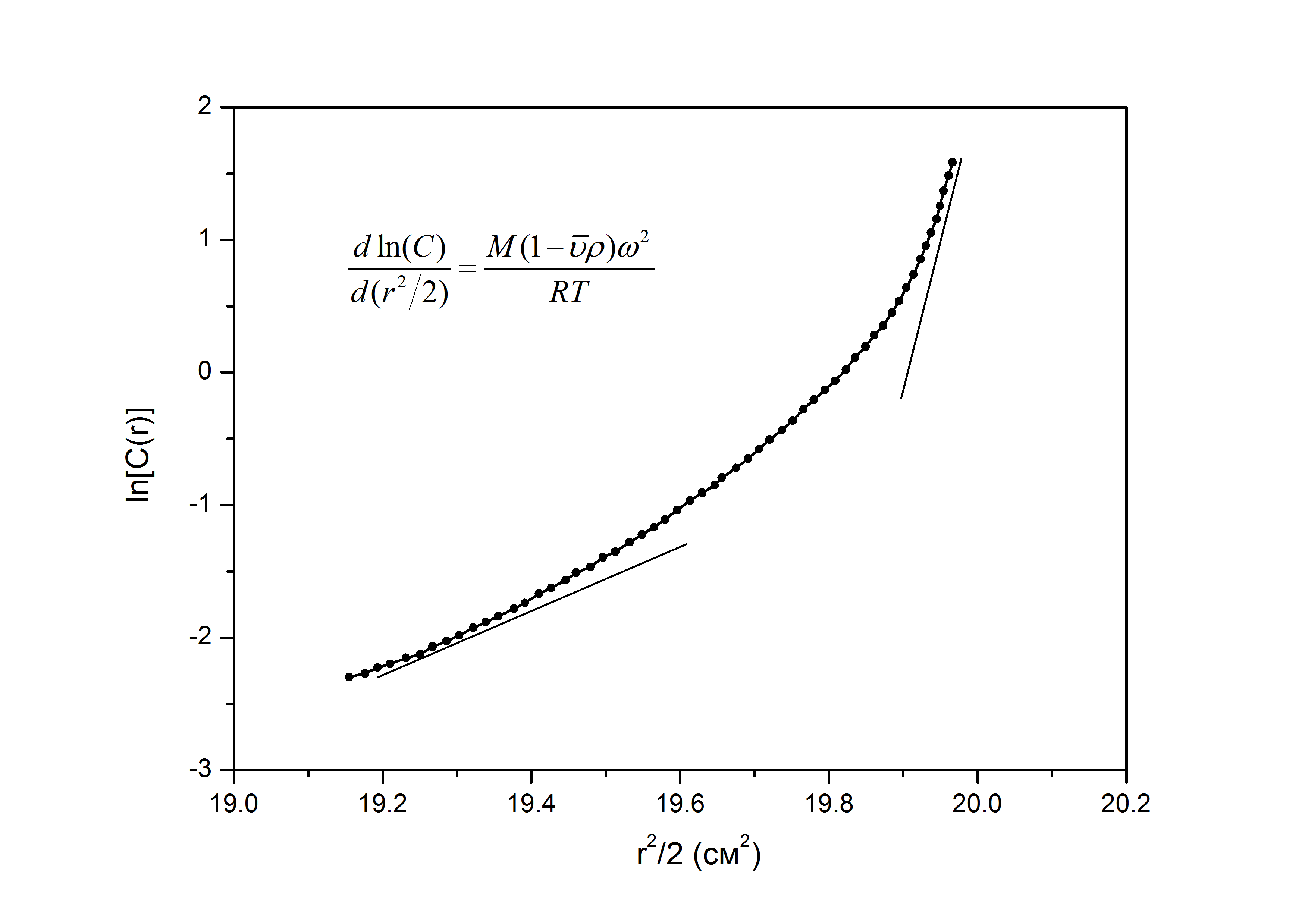Рис. 25.1. a) Кривая зависимости логарифма равновесной концентрации от квадрата радиуса для монодисперсных растворов макромолекул. Наклон кривой пропорционален молекулярной массе макромолекулы. б) Кривая логарифма равновесной концентрации против квадрата радиуса для раствора полидисперсных макромолекул. Нелинейность кривой означает полидисперсность раствора.

В первом случае угол наклона прямой линии пропорционален молекулярной массе. В полидисперсных растворах, содержащих макромолекулы различной молекулярной массы, каждая из них будет распределяться в соответствии с уравнением 25.3. Макромолекулы с наибольшей молекулярной массой концентрируются у дна ячейки, а с малой молекулярной массой – у поверхности, и поэтому кривая зависимости ln[C(r)] от r²/2 имеет изгиб направленный вверх. Тангенциальный наклон в каждой точке кривой дает значение молекулярной массы в соответствующей точке ячейки, а усреднение по нескольким точкам дает среднюю массу. Понятие среднего значения молекулярной массы пришло в биохимию из химии полимеров и использовалось и используется до сих пор для характеристики полидисперсности образцов. Вычисление среднего значения молекулярной массы для полидисперсных растворов базируется на разном способе подсчета суммарной массы разных компонентов. Если вычисление основано на численном усреднении, то такой тип среднего значения известен как средне-численная молекулярная масса, M_n:

M_n = ∑N_im_i/∑N_i= ∑n_im_i (25.4)

где n_i есть численная доля молекул с молекулярной массой m_i.

Средне-весовая молекулярная масса M_w определяется как:

M_w = ∑N_im²_i/∑N_im_i=∑w_im_i (25.5)

где w_i есть массовая доля молекул с массой m_i.

Отношение M_w/ M_n является мерой полидисперсности системы. Если это отношение сильно отличается от единицы, то массы в смеси отличаются очень сильно. Например, для смеси из двух молекул с массами отличающимися в десять раз (10 000 Дa и 100 000 Дa), M_n= 55 000 Дa, a M_w= 91 818 Дa, и их отношение равно 1.67. Если это отношение меньше 1.1, то это означает, что молекулы в смеси имеют близкие молекулярные массы.

Вернемся к уравнению 25.3 и обратим внимание на то, что в него не входит форма молекулы. В этом особенность метода седиментационного равновесия. Форма макромолекулы действует только на скорость, с которой устанавливается равновесие, а не на конечный результат.

Уравнение 25.3 может быть использовано для оценки скорости вращения ротора, необходимого для установления равновесия. Со стандартными оптическими системами точное измерение может быть выполнено, когда концентрация понижается в два раза на 1 мм длины ячейки с образцом а. Если молекулярная масса частицы равна 50 000 Дa, а = 6 см, и = 0.75 см³·г^-1, тогда ω = 1000 радиан·сек^-1 или 10400 об·мин^-1. На рисунке 25.2 графически представлены оптимальные скорости для достижения равновесия, если молекулярная масса или коэффициент седиментации образца приблизительно известен.

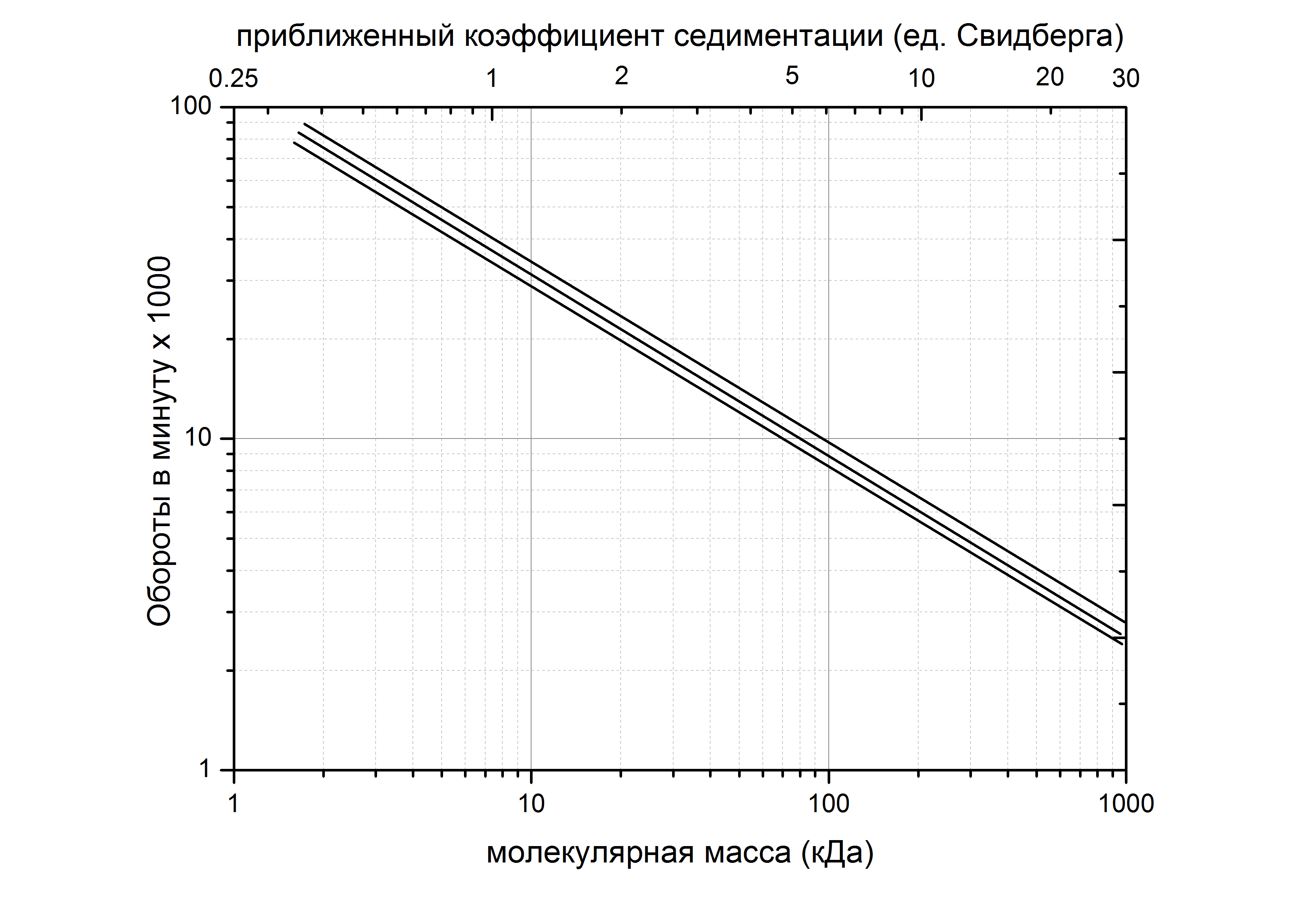
Рис. 25.2. Рекомендуемая оптимальная скорость, при которой достигается равновесие, для молекул с известными молекулярной массой или константой седиментации