Вязкость, как локальные потери энергии

Внутреннее трение или вязкость жидкости проявляется тогда, когда она находится в состоянии потока с отличным от нуля градиентом скорости. Самым простым примером является ламинарный поток с постоянным градиентом скорости G = под прямым углом по отношению к потоку (рис. 21.1).

Рис. 21.1 Скорость и градиент распределения скорости в ламинарном потоке в бесконечно малом зазоре между цилиндрами

Напоминаем, что условия ламинарного потока выполняются тогда, когда жидкость, наблюдаемая в эксперименте, течет медленно между двумя параллельными поверхностями. В этом случае η₀ не зависит от G и такой поток по своим вязкостным свойствам называется ньютоновым. При достаточно высокой скорости свойства потока начинают изменяться. Такой поток называется турбулентным. В этом случае η₀ начинает зависеть от G и такой поток называется неньютоновым. В цилиндрических трубах переход от ламинарного потока к турбулентному происходит, когда число Рейнольдса достигает значения 2000 (рис. 21.2).

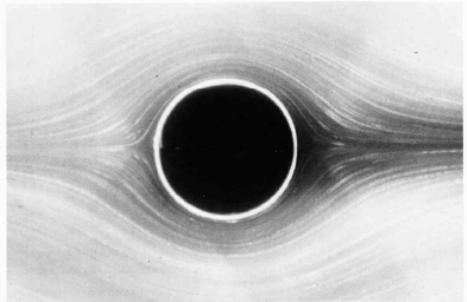
Рис. 21.2. Движение цилиндра в жидкости при разных числах Рейнолдса (слева направо: 0.16, 2000,10000). Изображения взяты из An album of fluid motion

Поток жидкости в узких капиллярах или протекающий между двумя медленно вращающимися цилиндрами, расположенными близко друг к другу, является ламинарным потоком при любых скоростях, необходимых для измерения вязкости

Скорость жидкости u в ламинарном потоке находится из выражения:

(21.1)

Вязкость жидкости является мерой внутреннего трения, которое определяет значение тангенциальной силы F, необходимой для поддержания градиента скорости G между плоскостями жидкости. Чем большим внутренним трением обладает жидкость, тем большую силу надо приложить к ней с тем, чтобы поддерживать в потоке заданный градиент скорости G. Эта связь выражается формулой Ньютона:

(21.2)

Константа пропорциональности называется коэффициентом вязкости или просто вязкостью жидкости. Её размерность – дина·сек^-1·см^-2 или эрг·см^-3·сек^-1. Таким образом, вязкость может быть определена как потери энергии на единицу объема за единицу времени в потоке с единичным градиентом скорости. Для поддержания градиента скорости G в жидкости, должна быть затрачена энергия. Чтобы вычислить ее, рассмотрим два слоя - 1 и 2, разделенных третьим, толщиной dy над участком поверхности хy и площадью 1 см² (рис. 21.1). За время t смещение слоя 2 относительно слоя 1 в х-направлении будет равно:

Таким образом, в слое толщиной dy и площадью 1 см² проделанная работа будет равна: dA = Fdx= F Gtdy для объёма жидкости, равного dy∙см². При этом количество проделанной работы для преодоления трения на единицу объема равно: A = F·G·t. Подставляя F из уравнения 21.2, получаем выражение для проделанной работы за единицу времени на единицу объема, обусловленное направленным потоком:

(21.3)

Это выражение является центральным в обсуждении вязкости макромолекул. Из него видно, что проделанная работа всегда пропорциональна квадрату градиента скорости.