28 Лекция 4 лекция 4. Теория вращательного трениЯ Вращательное движение в одном измерении
Мы начинаем эту Лекцию с обсуждения вращательной диффузии в одном измерении, поскольку это позволит нам провести нам аналогию с явлением поступательной диффузии. Вращательное движение частицы может быть описано как движение в одном измерении, если движение каждой точки частицы есть простое вращение вокруг одной оси, которая проходит через центр тяжести частицы (рис. 20.1). Движение такого типа может быть описано одним углом θ между соответствующими осями частицы (в нашем случае это линия, проходящая через длинную ось палочки) с любой другой подходящей осью в пространстве (в нашем случае это горизонтальная линия). Изменение θ во времени может быть выражено в терминах угловой скорости ω = dθ/dt.
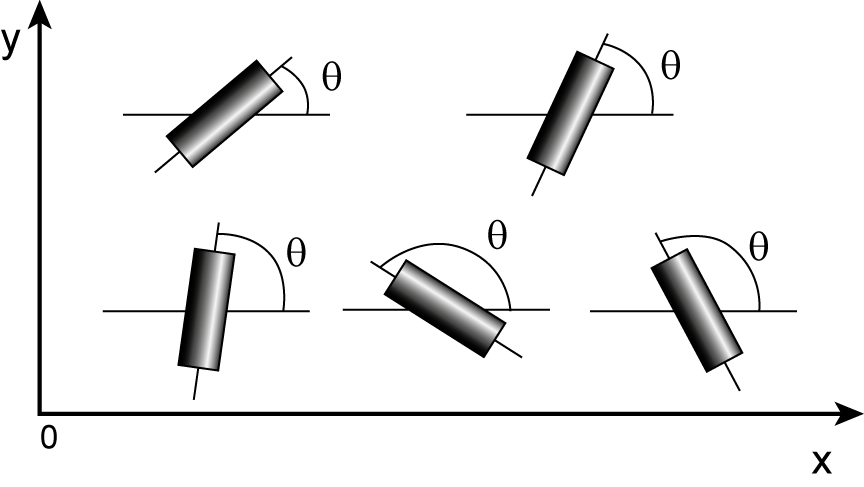
Рис. 20.1. Одномерное вращение. Все палочки лежат в xy плоскости. Вращение происходит вокруг z-оси, которая перпендикулярна плоскости xy. Вращательное движение палочки может быть описано одним параметром, углом θ
Теперь введем переменную величину ρ(θ), таким образом, что число частиц в 1 см3 раствора, обладающих ориентацией между углами θ и θ + dθ будет равно ρ(θ)dθ. Физический смысл этой величины очень прост. В равновесном состоянии все значения угла θ будут равновероятны и величина ρ(θ) будет постоянной. В неравновесном состоянии под влиянием вращающего момента некоторые ориентации становятся предпочтительными и значение ρ(θ) становится зависимым от θ. Если вращающий момент, производящий ориентацию молекулы, удалить, то система постепенно теряет преимущественную ориентацию и, в конце концов, ρ(θ) снова становится постоянной. Этот процесс называется вращательной диффузией.
Связь между коэффициентами вращательного трения и коэффициентом вращательной диффузии:
Θ = kT/ζ (20.5)
Вращательное движение и время релаксации
Многие трехмерные проблемы удобнее рассматривать при помощи представления о времени релаксации, которое мы сейчас определим. Предположим, что у нас есть набор макромолекул в растворе и некоторое выделенное направление жестко связанное с молекулой. Поскольку молекулы распределены в растворе хаотически, то все возможные направления равновероятны (рис. 20. 2 a). Допустим, что за какое-то короткое время мы сможем сориентировать макромолекулы в заданном направлении, используя, например, силу электрического поля (рис. 20.2 б).
Рис. 20.2. Различные состояния макромолекул в растворе. (а) все молекулы расположены случайным образом; (б) все молекулы ориентированы вертикально; (в) некоторые молекулы частично разориентированы (г) полная (случайная) разориентация. Примечание: интервал времени между состояниями (б) и (в) – короткий, временной интервал между (в) и (г) – длинный по отношению к вращательным свойствам макромолекул
После выключения поля и, следовательно, исчезновения действия ориентирующей силы через короткое время наступит частичное нарушение ориентации, как показано на рисунке 20.2 в. Для того, чтобы охарактеризовать стадии (б) и (в) мы введем угол, θ, который будет характеризовать связь между исходной ориентацией молекулы в положении (б) и новым направлением в положении (в). Среднее значение косинуса этого угла <cosθ> может служить мерой ориентации молекулы; <cosθ> равен единице, когда все молекулы полностью ориентированы и стремится к нулю, когда ориентация беспорядочная (рис. 20.2 г). Время, необходимое для перехода системы от состояния (б) к состоянию (г) называется временем релаксации системы. Итак, время релаксации, τ, которое определяется уравнением
<cosθ>t/<cosθ>t=0 = e–t/τ (20.8)
является временем, необходимым для того, чтобы значение <cosθ> уменьшилось до 1/e от его начальной величины.
В таких экспериментальных методах как электрическое двойное лучепреломление, деполяризованная флуоресценция наблюдаемые эффекты всегда описываются мультиэкспоненциальными функциями, содержащими до пяти времен релаксации. Однако, экстракция пяти времен релаксации и соответствующих им пяти амплитуд из экспериментально измеренного времени спада невозможна. Причина этого лежит в том, что с математической точки зрения разложение такого рода относятся к некорректно поставленным или плохо обусловленным задачам. Упрощение этой проблемы приводит к двум временам: к «среднему времени релаксации», которое определяется как взвешенное арифметическое среднее из пяти времен релаксации и к «начальному времени релаксации», которое определяется как взвешенное гармоническое среднее всех релаксационных времен.
Вращение твердого объекта в вязкой жидкости сопровождается также вращением молекул растворителя относительно друг друга. Молекулы растворителя, находящиеся вблизи вращающейся частицы, оказываются возмущенными в наибольшей степени. Это возмущение исчезает при удалении молекул растворителя от частицы. У поверхности сферы молекулы растворителя движутся вместе со сферой, в соответствии с граничными условиями полного прилипания. Линии потока при поступательном движении уменьшается относительно более медленно, чем возмущение при вращательном движении.
Вращательное трение гораздо более чувствительно к размеру частицы, чем поступательное. Причина этого лежит в том, что величина ζ0 пропорциональна кубу линейных размеров молекулы, тогда как величина f зависит от линейных размеров в первой степени.
Таблица 20.1 Константы вращательной диффузии некоторых макромолекул в воде.
Макромолекулы |
Θ (сек-1) |
Грамицидин (димер) Лизоцим Кинезин (349) Фрагмент ДНК (104 п. о.) T7 бактериофаг Вирус табачной мозаики ДНК бактериофага T7 ДНК бактериофага T4 |
60 000 000 16 700 000 5 000 000 172 000 5 290 330 5.2 0.41 |
Вращательные коэффициенты диффузии некоторых биологических молекул (от грамицидина до ДНК из бактериофага Т4) представлены в таблице 20.1. Интервал их значений, составляет восемь порядков, что во много раз превосходит таковой для коэффициентов поступательной диффузии или коэффициентов седиментации. Причина этого с физической точки зрения проста: поступательное трение пропорционально линейным размерам частицы, а вращательное – кубу линейных размеров (объему).
Эллипсоид вращения
Для эллипсоида вращения с осями a, b = c существует не один, a два коэффициента трения: один, ζa – для вращения вокруг полуоси a, а второй, ζb – для вращения вокруг полуоси b. На практике очень трудно измерить величины ζa и ζb. независимо. Поэтому обычно вычисляют среднее значение коэффициента вращательного трения ζ и среднее значение коэффициента вращательной диффузии Θ по уравнениям:
ζ = 6η0V/J(p) (20.13)
Θ = kT J(p)/6η0V (20.14)
где 1/J(p) – функция Перрена, которая зависит от отношения осей эллипсоида вращения. Теоретическое значение 1/J(p) представлено в виде графика на рисунке 20.3. Сравнение зависимостей вращательного трения, представленных на рисунке 20.3, с таковыми для поступательного трения (рис. 19.2) показывает, что вращательное трение гораздо более чувствительно к форме молекулы, чем поступательное трение. Кроме того, коэффициенты вращательного трения более чувствительны к изменениям граничных условий. Так, при переходе от условий скольжения к условиям прилипания поступательное трение изменяется только в 1.5 раза. Однако при таком же переходе при вращательном движении имеет место другая ситуация. Для вытянутого эллипсоида в условиях скольжения нет сопротивления при вращении его вокруг длинной оси, а для сплюснутого – вокруг короткой.
Рис. 20.3. Зависимость усредненного по ориентациям коэффициента вращательного трения ζ от отношения осей вытянутого и сплюснутого эллипсоидов. Эта гидродинамическая функции вычислена с помощью компьютерной программы
Для вытянутого эллипсоида вращения с полуосями a и b (a > 5b), вращение вокруг одной b оси хорошо описывается уравнением:
(20.15)
из которого видно, что малая ось b появляется под знаком логарифма. Отсюда следует, что её вклад в величину Θ относительно мал и, следовательно, константу вращательной диффузии следует использовать для вычисления длинной, а не короткой оси эллипсоида.
Круговой цилиндр
Напоминаем, что круговой цилиндр относится к телам, для которыx константа вращательного трения (или диффузии) не может быть представлена в аналитическом виде. Причина этого – наличие краевых эффектов, которые мы обсуждали ранее (Лекция 17). Поэтому, константа вращательной диффузии круговых цилиндров (палочек) обычно выражается как:
(20.16)
где η0 – вязкость растворителя, kT – тепловая энергия, L – длина палочки, d – ее диаметр и γ – фактор трения, который зависит от способа учета краевых эффектов. Как и в случае эллипсоида вращения диаметр палочки, d, появляется в уравнении (20.16) только под знаком логарифма и поэтому константу вращательной диффузии следует использовать в первую очередь для вычисления длины кругового цилиндра.