Определение фрикционных свойств частиц

Граничные условия: «полное прилипание» и «свободное скольжение»

В теории гидродинамики взаимодействие частицы с растворителем обычно рассматривается при двух граничных условиях: «полное прилипание» и «свободное скольжение».

В случае свободного скольжения, молекулы растворителя не взаимодействуют с поверхностью частицы, и частица перемещается или вращается в нем независимо от молекул растворителя (рис. 18.3 a). Другой крайний случай представлен "полным прилипанием", при котором первый слой растворителя примыкает к поверхности частицы и перемещается (вращается) вместе с ней (рис. 18.3 б).

Важно отметить, что значения констант в уравнениях, связывающих измеренные величины с вычисляемыми гидродинамическими параметрами, сильно зависят от выбора граничных условий.

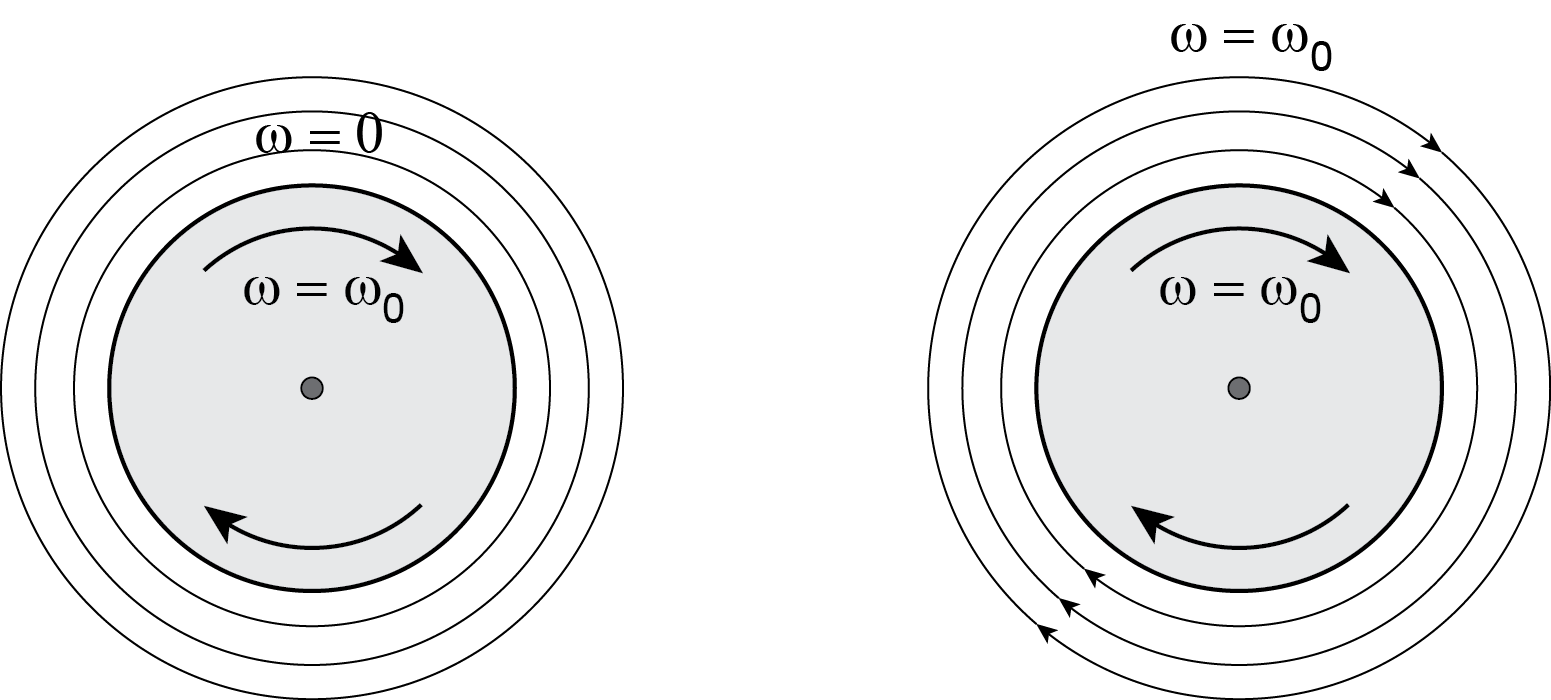
а) б)

Рис. 18.3 Гидродинамическое представление условий скольжения (a) и прилипания (б), где ω – частота вращения

В литературе можно найти утверждения, что для молекул белков с молекулярной массой 2000 Дa и менее в большей степени приемлемы граничные условия свободного скольжения, тогда как для молекул белков с молекулярной массой 5000 Дa и больше более обоснованы условия полного прилипания. Этот вопрос носит принципиальный характер, поскольку связан с нижней границей применения гидродинамических уравнений и будет обсужден подробно в этой части.

Гидродинамические эксперименты

Эксперименты в гидродинамике можно разделить на четыре группы. В первую группу входят эксперименты, в которых измеряется стационарная скорость движения частиц под действием некоторой силы. Если движущей силой является градиент концентрации макромолекул, то такое явление называется трансляционной диффузией. Когда действующая сила имеет гравитационную природу, то такое явление называется седиментацией. Если на частицу действуют силы электрической природы, то явление называется электрофорезом.

Вторая группа включает эксперименты, в которых вращение частиц осуществляется под действием на них пары сил. Если градиент скорости в растворителе играет роль ориентирующей силы, то такое явление известно под названием эффекта Максвелла или двулучепреломления в гидродинамическом потоке. Если ориентирующая сила имеет электрическую природу, то явление называется эффектом Керра или двулучепреломлением в электрическом поле.

Третья группа представлена экспериментами, измеряющими потерю энергии, обусловленную трением молекулы в растворе. Это явление называется вязкостью.

К четвертой группе мы относим явления, в которых на частицу не действуют никакие внешние силы и их перемещение и вращение происходят только под влиянием теплового воздействия, связанного с броуновским движением. Поведение частиц в экспериментах по флуоресценции и динамическому рассеянию света имеет такую природу.

Таблица 18.1. Гидродинамические методы, используемые в молекулярной биофизике

Экспериментальный метод	Измеряемые величины	Вычисляемые параметры
Трансляционная диффузия	Коэффициент трансляционной диффузии	Коэффициент поступательного трения
Скоростная седиментации	Коэффициент седиментации	Коэффициент поступательного трения
Электрофоретическая подвижность	Электрофоретическая подвижность	Коэффициент поступательного трения
Флуоресцентная корреляционная спектроскопия	Время диффузии	Коэффициент поступательного трения
Восстановление свечения красителя после выцветания	Время диффузии	Коэффициент поступательного трения
Прямые гидродинамические модельные эксперименты	Прямое определение коэффициента поступательного трения
Ориентация молекул в электрическом поле (эффект Керра) и в гидродинамическом потоке (эффект Максвелла)	Угол ориентации и величина двойного лучепреломления	Коэффициент вращательного трения
Деполяризованная флуоресценции	Коэффициент деполяризации	Коэффициент вращательного трения
Динамическое рассеяние света	Корреляционная функция и флуктуации числа частиц	Коэффициенты поступательного и (или) вращательного трения
Вязкость	Удельная вязкость	Характеристическая вязкость

В таблице 18.1 в первой колонке перечислены гидродинамические методы, используемые в настоящее время, а в третьей представлены параметры, которые могут быть вычислены на их основе. Измеряемые величины представлены во второй колонке. Следует заметить, что, несмотря на разнообразие представленных методов, только три параметра могут быть вычислены из гидродинамических опытов: коэффициенты поступательного и вращательного трения, а также характеристическая вязкость.

В таблице 18.1 приведен также метод, который мы называем методом гидродинамического моделирования. В этом методе определяют фактический коэффициент трения частицы, наблюдая за движением ее макроскопической модели в растворителе с высокой вязкостью с тем, чтобы обеспечить измерения при маленьких числах Рейнольдса. Следует отметить, что в таких экспериментах коэффициент трения модели определяют прямым способом, без каких-либо промежуточных уравнений или вычислений.