6.2. Методология эксперимента

В силу сложности экспериментальных исследований, прежде чем приступить к ним, необходимо разработать методологию эксперимен­та. Методология эксперимента — это концепция, общие принципы, структура эксперимента, его постановка и последовательность выпол­нения экспериментальных исследований.

Цель разработки методологии эксперимента — это экономия мысли и труда. Одним из направлений, позволяющим осуществить сформули­рованную цель, служит применение математических методов планирова­ния эксперимента. По определению В.В. Налимова, «планирование экс­перимента — это оптимальное управление экспериментом при неполном знании механизма явления» [20, с. 273]. Математические методы планирования эксперимента позволяют исследовать и оптимизировать сложные систе­мы и процессы, обеспечивая высокую эффективность эксперимента и точность определения исследуемых факторов.

Планирование эксперимента рассматривается как одно из направ­лений кибернетики, так как во многих случаях, приступая к изучению некоторого объекта, исследователь не знает всех тонкостей механизма его функционирования. Тогда, основываясь на принципах кибернети­ки, объект в целом или его элементы можно представлять в виде «черного ящика». В основу планирования эксперимента положе­ны принципы теории эксперимента, такие как последовательность про­ведения, рандомизация, оптимальное использование факторного про­странства и математическое моделирование.

Последовательное проведение эксперимента означает, что его выпол­няют поэтапно: анализируются данные каждого этапа и принимается решение о целесообразности приведения дальнейших исследований. Результаты эксперимента представляются уравнением регрессии или моделью процесса. С позиции кибернетики под моделью понимают приближенное выражение неизвестного закона, которое удовлетвори­тельно характеризует явление в некоторой локальной области фактор­ного пространства.

Принцип рандомизации заключается в том, что в план эксперимен­та вводят элемент случайности. Для этого план эксперимента состав­ляют таким образом, чтобы те систематические факторы, которые труд­но поддаются контролю, учитывать статистически и исключить в исследованиях как систематические ошибки.

Принцип оптимального использования факторного пространства зак­лючается в снижении размерности задачи за счет выявления ненаблю­даемых параметров, являющихся линейной комбинацией наблюдаемых (измеряемых) параметров — факторов. Это позволит добиться значи­тельного увеличения точности расчета коэффициентов полученной модели и уменьшить трудоемкость эксперимента.

Планы «оптимального эксперимента» реализуются в следующей последовательности:

1. оценка информации и определение факторов, наиболее суще­ственных для исследуемого процесса;

2. использование математической модели в виде линейной функ­ции отклика;

1. анализ выбранной модели;

3. нахождение экстремума в области n-мерного факторного про­странства путем использования полинома k-Pi степени;

Логически выстроенная последовательность этапов применения специальных положений, правил, методов, способов и приемов иссле­дования для достижения цели эксперимента отображается в виде ме­тодики эксперимента. Число этапов и содержание исследований зави­сят от способа изучения объекта. Перейдем к изучению содержания этапов в понятиях классического и вычислительного экспериментов.

Классический эксперимент

Процесс выполнения классического (материального) эксперимента структурируется в шесть последовательно выполняемых этапов [20, с. 275].

Этап I. Постановка проблемы, обоснование целей и задач эксперимента. Содержание первого этапа зависит от того, какой проблемой обусловлен эксперимент, т.е. совершенствование, развитие или реорганизация системы управления. Отметим некоторые его особенности. Обоснование цели и задач эксперимента основывается на анализе собранной информации, выдвинутой гипотезе и теоретических разработках. Цель должна определять ожидаемые результаты исследования, а задачи — промежуточные результаты, которые будут получены по отдельным этапам исследования.

Этап II. Формализация изучаемой реальности. Началом изучения объекта эксперимента следует считать:

а) построение его структурной модели с использованием принципов кибернетики и процессного подхода;

б) сбор, изучение и анализ имеющихся данных об объекте;

в) определение входных X (экзогенных) и выходных Y (эндогенных) параметров также параметров преобразования (управляемых переменных) — Z.

Этап III. Обоснование средств и требуемого количества измерений или наблюдений, которые рассматриваются в качестве источников сбора информации. Для измерения в первую очередь используются стандартные, серийно выпускаемые приборы и аппараты.

В отдельных случаях возникает потребность в создании уникальных средств измерения.

Этап IV. Проектирование процесса проведения эксперимента. В начале составляют последовательность (очередность) проведения измерений и наблюдений в приложении к структурной модели объекта. Затем каждую операцию измерения описывают с учетом выбранных измерительных средств. Большое внимание уделяют методам контроля качества операций, записи результатов наблюдений и измерений.

Этап V. Планирование эксперимента. Планирование эксперимента необходимо во всех случаях, когда еще перед началом исследования предварительные знания можно представить (задать гипотезу) математической моделью. Планирование эксперимента начинается с выбора варьируемых факторов и установления основных и второстепенных, влияющих на исследуемый процесс.

Этап VI. Выбор методов обработки и анализа экспериментальных данных. Обработка данных сводится к систематизации всех чисел, клас­сификации и анализу. Результаты экспериментов должны быть сведе­ны в удобные формы записи — таблицы, графики, формулы, номо­граммы, позволяющие быстро сопоставить полученные результаты. Особое внимание должно быть уделено математическим методам об­работки опытных данных — аппроксимации каким-либо видом эмпи­рической зависимости, проверке адекватности модели, нахождению критериев и доверительных интервалов.

Вычислительный эксперимент

Принципиальное отличие вычислительного эксперимента от клас­сического состоит в том, что он проводится не с реальной системой, а с ее моделью. В этом контексте особенно заслуживают внимания ими­тационные эксперименты. Под вычислительным экспериментом пони­мается численный метод проведения экспериментов с математически­ми и имитационными моделями, описывающими поведение сложных систем в некоторый период времени. В процессе вычислительного эк­сперимента исследователь имеет дело с тремя основными моделями (рис. 12):

1. реальным объектом (система);

2. имитационной моделью объекта;

3. информационно-вычислительной системой (ИВС).

В понятие «имитационная модель объекта» (или имитация) при вычислительном эксперименте вкладывается широкий смысл. Здесь понимается не только «чисто» имитационная модель, но и комплекс математических моделей, описывающих функционирование системы разной природы. Таким образом, вычислительный эксперимент — это всегда имитация некоторой реальности.

Область применения вычислительных экспериментов в экономике и управлении простирается от имитации конкретных видов деятель­ности до имитации функционирования корпорации и даже экономи­ки страны с применением различного класса моделей. Об этом свиде­тельствуют исследования Т. Нейлора и его коллег из Университета социальных систем и имитационного моделирования, а также раз­работки в области моделирования экономики, управления и практического менеджмента — деловые игры, «case — stade» и практические управленческие задачи. Вычислительные эксперимен­ты позволяют исследовать все то, что не подвластно классическому эк­сперименту, а именно:

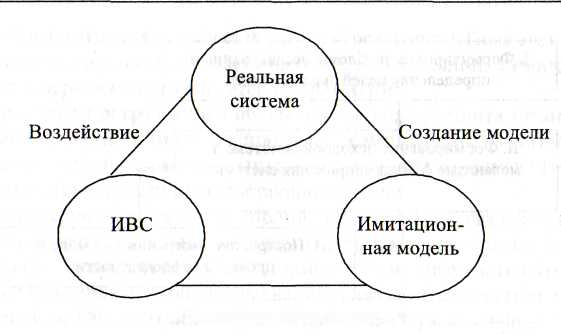
Экспериментирование

Рис. 12. Агрегированная структура вычислительного эксперимента

а) изучить сложные внутренние взаимодействия подсистем и эле­ментов системы и воздействие на их функционирование различного характера изменений во внешней среде;

б) вскрыть важные особенности в функционировании системы и разработать предложения по ее совершенствованию;

в) получить новые знания, изучить и оценить новые ситуации, рас­полагая неполной информацией о событиях будущего;

г) проработать варианты стратегий и политики и предсказать узкие места и другие трудности до их фактического применения.

Схема основных этапов вычислительного эксперимента, составлен­ная с учетом рекомендаций из публикаций, приводится на рис. 13.

Дадим краткое пояснение выделенным на рис. 13 этапам вычис­лительного эксперимента. Как и любое исследование, вычислитель­ный эксперимент начинается с формулировки проблемы (этап I) и яс­ного изложения целей эксперимента. Цели эксперимента задают в виде:

• рабочих гипотез, которые надо проверить;

• вопросов, на которые надо ответить;

• управляющих воздействий, которые надо оценить.

Построению базовой модели всегда предшествует принятие гипоте­зы об особенностях функционирования исследуемой системы (этап II), например она динамическая или статическая, детерминированная или вероятностная, характер ее функционирования непрерывный или дис­кретный.

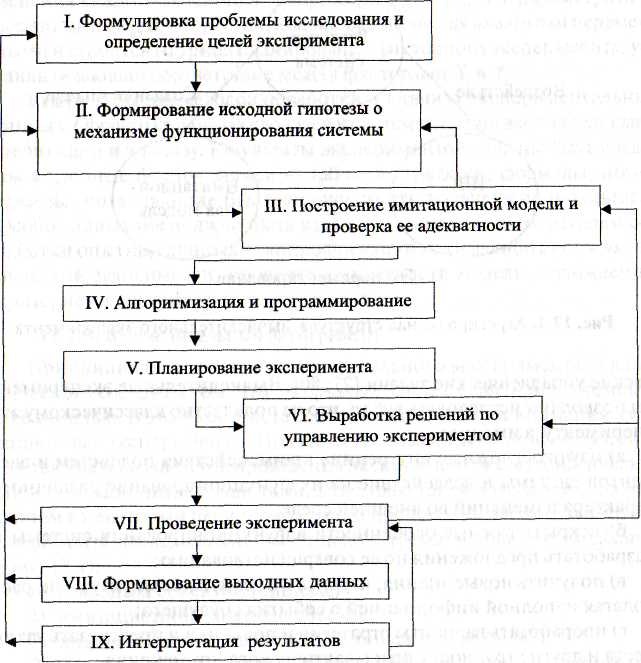
Рис. 13. Содержание и последовательность этапов вычислительного эксперимента

При построении имитационной модели системы (этап III) возни­кает несколько проблемных вопросов:

1. о сложности модели — надо строить такие математические модели, которые давали бы точное описание поведения системы и не тре­бовали бы сложного программирования и вычисления;

2. о продолжительности программирования и вычислений на ком­пьютере — эксперимент должен проходить за приемлемое для иссле­дователя время;

3) об адекватности модели описываемой реальности. Пока этот воп­рос не решен, ценность модели остается незначительной, а имитаци­онный эксперимент превращается в упражнение.

Разработка программного обеспечения эксперимента (этап IV) включает создание комплекса программ компьютерной имитации, организацию данных и начальных условий функционирования систе­мы, а также генерирование недостающих данных.

Наиболее сложная задача, выполняемая на этапе V, связана с пла­нированием вычислительного эксперимента, так как тип плана экспе­римента всегда зависит от поставленной цели и исследуемого объекта. В теории планирования эксперимента есть два важных понятия: фак­тор и реакция. Оба термина относятся к переменным. Фактор — экзо­генная или управляющая переменная, реакция — эндогенная (выход­ная) переменная. Анализ факторов при выполнении вычислительных экспериментов производится по следующей общепринятой схеме.

1. Управляем ли рассматриваемый фактор?

2. Наблюдаемы ли (измеряются, регистрируются, фиксируются) значения фактора?

3. Составляет ли влияние фактора предмет изучения или он вклю­чен только для увеличения точности эксперимента?

4. Являются ли уровни фактора количественными или качествен­ными?

5. Является ли фактор фиксированным или случайным? Планирование вычислительного эксперимента проводится с целью сокращения числа вычислительных прогонов и их продолжительнос­ти, количества наблюдаемых переменных, шагов изменения парамет­ров и т.д. Не исключаются случаи, когда исследователь отказывается строго фиксировать схему проведения эксперимента. Принимаемая им стратегия предусматривает возможность принятия решений в зависи­мости от результатов, получаемых на отдельных этапах исследования. Например, исследователь, в зависимости от априорных сведений и ра­нее полученных результатов, прибегает последовательно к различным методам нахождения решения: линейному приближению, описанию полиномами второго, а иногда и третьего порядка и т.д. Здесь каждый последующий шаг определяется ранее полученными результатами. Планирование вычислительного эксперимента сопровождается рядом таких проблем, как «проблема объема» или проблема слишком боль­шого количества факторов, проблема выбора плана эксперимента в соответствии с его целью, проблема многокомпонентной реакции, порождающая проблему оценки результатов имитационного моделирования. Планирование вычислительного, как и любого другого, экс­перимента заслуживает специального изучения.

Выработка решений по управлению экспериментом (этап VI) ос­нована на оценке исходной гипотезы о поведении исследуемой систе­мы и отладке имитационной модели и построении алгоритма (блок-схемы) организации эксперимента.

Имитационный эксперимент (этап VII) — это проведение серии имитационных расчетов в системном масштабе времени и по разрабо­танному алгоритму. Каждая реализация модели отличается от другой только в одном изучаемом аспекте. Таким образом, в результате ими­тационного эксперимента образуются ряды статистических данных (выборки), обработка которых требует определенных знаний.

После того как эксперимент проведен и получены результаты, воз­никает задача — представить эти результаты в компактной форме, вы­дать рекомендации и сделать заключение (этапы VIII и IX). Основным требованием к обработке (редукции) выходных данных служит извле­чение максимума информации. К основным методам обработки дан­ных относятся методы математической статистики: дисперсионный анализ (критерий F, методы множественных сравнений упорядочения), спектральный анализ и эвристические процедуры, основанные на оценке параметров статистических распределений. Применение идей и методов математической статистики резко сокращает объем экспери­ментальных исследований и, что самое главное, увеличивает четкость суж­дений исследователя о полученных результатах в ходе эксперимента.

Каждый рассмотренный этап классического и вычислительного экспериментов — это этап исследования, требующий от исполнителя специальных знаний, больших затрат интеллектуальных и временных ресурсов.