1.3. Метод начальных параметров

Запишем формулу (1.5) в виде

(1.9)

Если принять гипотезу, что EJ = const, то дифференциальное уравнение (1.9) даёт

Нагрузка q считается положительной, если совпадает с осью y, направленной вверх. При выводе уравнения метода начальных параметровбудем исходить из последней формулы

(1.10)

Первый участок.

Считаем, что на этом участке, , нагрузка постоянна, , рис.1.3.

Интегрируя уравнение (1.10) четыре раза, получаем

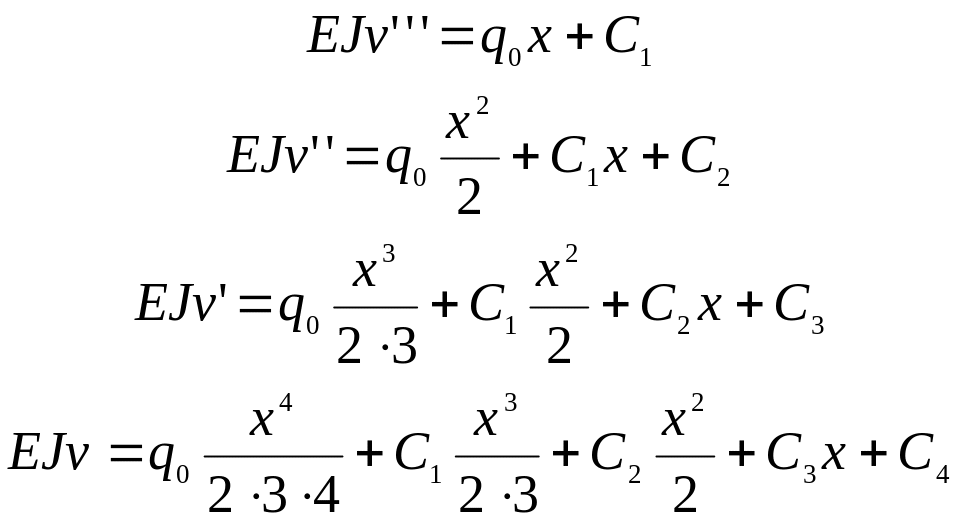(а)

Произвольные постоянные интегрирования будем искать из граничных условий в начале координат, при x = 0. Т.е. в начале координат прогиб равен , угол поворота , изгибающий момент , поперечная сила .

Подстановка граничных условий даёт

(1.11)

Их дальнейшая подстановка в (а) приводит последние к виду (формулы (б), слева)

Первый участок	Второй участок
		(б)

Рис.1.4

	Эпюра Q от P0 и P1
	Эпюра M от M0 и M1
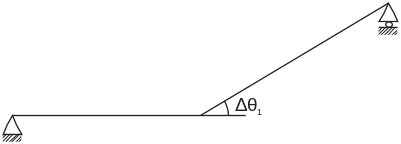
	Скачок в угле поворота
	Скачок в прогибе

Рис.1.5

Как видно из рис.1.4, интегрирование нагрузки q на втором участке представляет собой перекрещенную нижнюю площадь, равную , что написано слева в формулах (б), и перекрещенную верхнюю площадь, равную , что написано справа в формулах (б), где ещё добавлена произвольная постоянная в дополнение к , написанной слева. Дальнейшее интегрирование добавляет степень переменной и дополнительные постоянные интегрирования: .Рассмотрим их физический смысл.

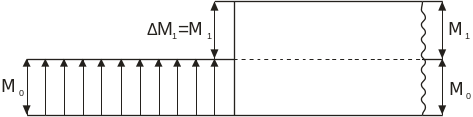
Произвольная постоянная представляет собой скачок в эпюре Q, вызванный внешней силой P₁. Соответственно - скачок в эпюре моментов, вызванный внешним моментом M₁. Скачки и показаны на чертеже, однако в рассматриваемых ниже балках они редко встречаются, поэтому их учитывать не будем.

Окончательная формула начальных параметров выглядит следующим образом

(1.11)

Здесь k – число промежуточных границ между началом и концом балки. Знак обозначает, что эти слагаемые следует принимать во внимание, если . Значок перед моментом M_i, поперечной силой Q_i и распределённой нагрузкой q_i обозначает скачок в опорах этих функций.

Рассмотрим несколько примеров.

Пример 1.

Рис.1.6	Рис.1.7

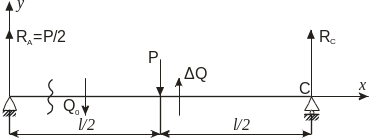
Определить перемещения и угол поворота балки, рис.1.6 в точке B.

Сначала определяем реакции в опоре и . Показываем внутренние усилия Q₀, M₀, ΔQ с учётом принятого правила знаков (рисунок справа). Составляем граничные условия.

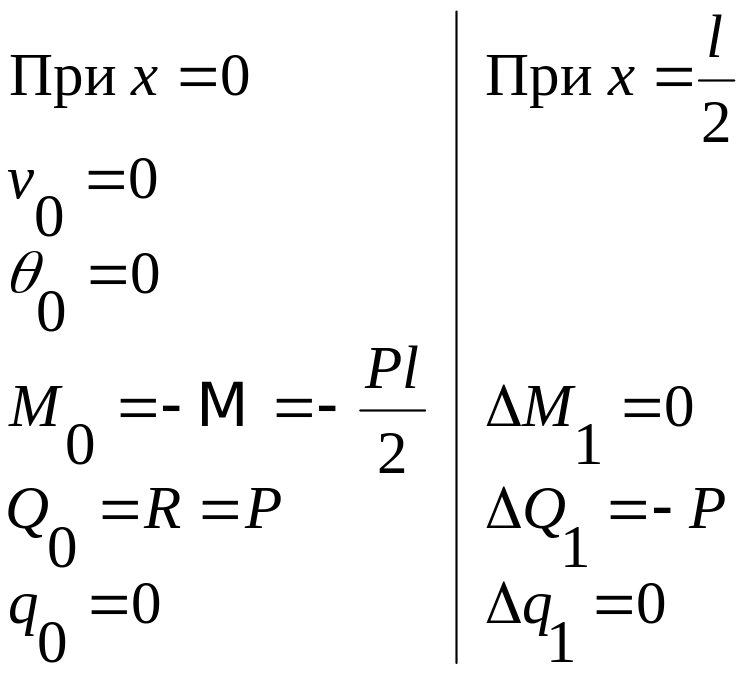
Подставляем их в уравнение (1.11)

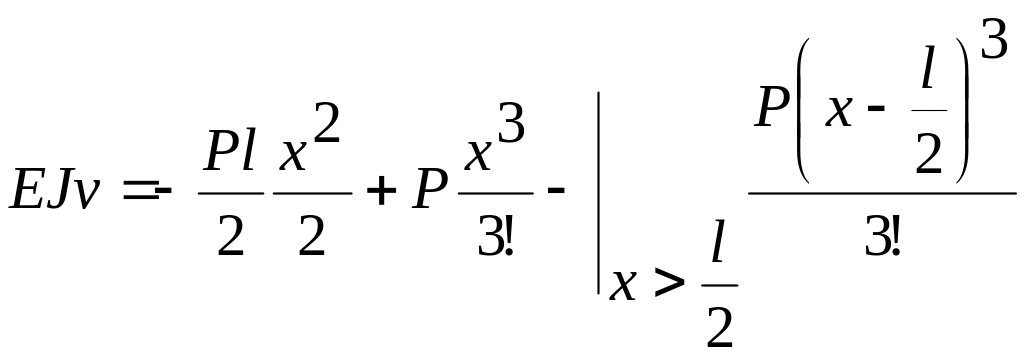(а)

Для определения прогиба в точке B подставляем сюда координату x=l.

Знак минус свидетельствует о том, что прогиб направлены в противоположную сторону оси y. Для определения угла поворота продифференцируем уравнение (а)

Подставляя координату точки B x=l, получим

Пример 2.

Определить прогиб балки в точке B и угол поворота в точке C, рис.1.8.

Рис.1.8

Сначала определяем реакции. Учитывая симметрию получаем и составляем граничные условия

Подставляем граничные условия в уравнение (1.11)

(б)

В этом уравнении остаётся неизвестной величиной (см. (1.11)), которую пытались определить из граничных условий в начале координат, при . Не удалось. Определим её из граничного условия при , где прогиб с помощью уравнения (б).

;

;

Подставив полученный результат в (б), получим окончательное уравнение

(в)

для поставленных задач. Для вычисления прогиба в точке B подставляем её координату

; .

Знак минус свидетельствует о том, что направление прогиба не совпадает с направлением оси y.

Для определения угла поворота необходимо продифференцировать уравнение (в)

Теперь подставляем в полученное уравнение координату точки C .

;