6.7.3 Сведение линейной краевой задачи к двум задачам Коши

Этот прием может быть использован для линейных краевых задач (6.20-6.22).

Будем искать решение уравнения (6.20) в виде

y(x) = Cu(x) + v(x). (6.29)

Потребуем, чтобы решение в форме (6.29) удовлетворяло (6.20) и граничному условию (6.21) при любом С.

Подставим (6.29) в (6.20):

С(u'' + pu' +qu) + v'' + pv' +qv = f.

Для того чтобы это уравнение выполнялось при любом C, необходимо, чтобы

u'' + pu' +qu = 0. (6.30)

Тогда v'' + pv' +qv = f. (6.31)

Подставим (6.29) в (6.21):

С[₁u(a) +₁u'(a)] + ₁v(a) +₁v'(a)=₁.

Аналогично: ₁u(a) +₁u'(a) = 0 

Этому граничному условию можно удовлетворить бесконечным числом способов. Например, можно потребовать, чтобы

u(a) = ₁K; u'(a) = –₁K. (6.32)

Таким образом, мы имеем задачу Коши (6.30), (6.32) для нахождения функции u(x). Оставшееся граничное условие для v(x)

можно выбрать так:

. (6.33)

Следовательно, для нахождения функции v(x) также имеем задачу Коши (6.31), (6.33).

Решая эти две задачи известными нам методами (например, Рунге-Кутта, Адамса), найдем функции u(x) и v(x) такие, что скомпонованная из них функция y(x) (6.29) будет удовлетворять (6.20) и (6.21).

Осталось удовлетворить (6.22). Подставим найденное решение в условие (6.22):

С[₂u(b) +₂u'(b)] + ₂v(b) +₂v'(b) = ₂ .

Из этого уравнения находим C:

.

Итак, решение краевой задачи закончено. Функция y(x) определена.

Видно преимущество этого подхода перед методом стрельбы. В методе стрельбы число задач Коши, которые нужно решить для получения искомого решения краевой задачи, определяется точностью удовлетворения граничному условию на правой границе.

При использовании этого метода необходимо решить только две задачи Коши.

6.7.4 Метод Ньютона для нелинейной краевой задачи

Этот метод заключается в сведении решения нелинейных задач к серии линейных задач.

Рассмотрим следующую краевую задачу.

y″ = f(x, y, y′), 0<x<1; (6.34)

y(0) = y₀; y(1) = y₁.

Пусть известна некоторая функция y₀(x), удовлетворяющая граничным условиям и грубо приближенно равная искомому решению y(x).

Положим

y(x) = y₀(x) + v(x), (6.35)

где v(x) – поправка к нулевому приближению y₀(x). Подставим (6.35) в (6.34) и линеаризуем задачу, используя равенства

y″(x) = y₀″(x) + v″(x);

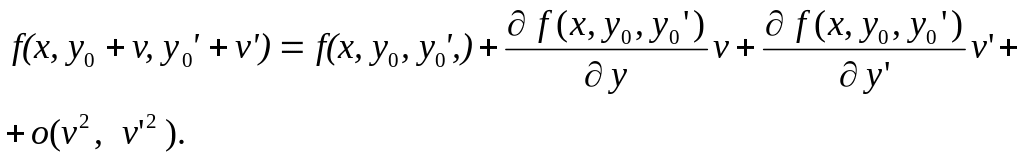Отбрасывая остаточный член второго порядка малости по v и v′, получим линейную краевую задачу для поправки :

(6.36)

где

Решая эту задачу, например, конечно-разностным методом с применением метода прогонки, найдем приближенно поправку и примем y₁(x) = y₀(x) + (x) за следующее приближение и т.д.

Литература

1. Демидович Б.П., Марон И.А. Основы вычислительной математики. Изд.3-е, испр., М.: Наука. Гл. ред. физ.-мат. лит., 1966.- 664 с.

2. Калиткин Н.Н. Численные методы. – Наука, 1978. – 512 с.

3. Марчук Г.И. Методы вычислительной математики. – М.: Наука, 1989. – 536 с.

4. Справочник по специальным функциям с формулами, графиками и математическими таблицами: Пер. с англ./ Под ред. М. Абрамовица и И. Стиган. – М.: Наука, Гл. ред. физ.-мат. лит., 1979.- 832 с.

5. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 600 с.

6. Самарский А.А., Гулин А.В. Численные методы. –М.: Наука, 1989. –432 с.

7. Самарский А.А. Введение в численные методы. – М.: Наука. Гл. ред. физ.-мат. лит., 1987. – 288 с.

8. Ортега Дж., Пул У. Введение в численные методы решения дифференциальных уравнений. М.: Наука. Гл. ред. физ.-мат. лит., 1986. – 288 с.

9. Боглаев Ю.П. Вычислительная математика и программирование. – М.: Высшая школа, 1990. – 534 с.

10. Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений. М.: Мир, 1980. – 280 с.

11. Арушанян О.Б., Залеткин С.Ф. Численное решение обыкновенных дифференциальных уравнений на Фортране. М.: Изд-во МГУ, 1990. – 336 с.

181