- •2.1. Определение наименьшего числа параллельно соединенных
- •2.2.Определение вероятностей безотказной работы звеньев в различных условиях эксплуатации.
- •2.3.Определение полных вероятностей безотказной работы
- •2.4. Определение вероятностей безотказной работы системы в различных условиях эксплуатации.
- •2.5.Определение полной вероятности безотказной работы системы.
- •2.6.Определение наиболее вероятных условий эксплуатации
- •2.7. Определение оптимального плана отыскания неисправного звена.
- •2.8.Определение математического ожидания числа проверок
- •2.9.Определение вероятностей отказа mi блоков из ni в каждом звене технической системы.
- •2.10. Определение числа резервных блоков.
- •2.13.Определение характеристик корреляционной связи
- •2.14.Определение характеристик регрессионной
2.9.Определение вероятностей отказа mi блоков из ni в каждом звене технической системы.
В соответствии с заданием расчет этих вероятностей необходимо провести для самых неблагоприятных условий эксплуатации. Здесь мы исходим из предположения о неизменности вероятности отказа блока во время эксплуатации, а также о независимости опытов, состоящих в отказе любого количества блоков из имеющихся в звене. Искомые вероятности находятся по известной формуле Бернулли
Pn(m) = C(n, m) ∙ pm ∙ (1 − p)(1 − m) |
(2.7) |
где Pn(m) − вероятность наступления некоторого события A ровно m раз в n независимых опытах, проводимых в одинаковых условиях; p − вероятность наступления события A в каждом опыте; C(n, m) − число сочетаний из n по m.
Заметим, что в комбинаторике сочетаниями называются такие соединения из n элементов по m, которые отличаются между собою самими элементами. Число сочетаний определяется по формуле
C(n, m) = n! / m! / (n − m)! |
(2.8) |
Наиболее неблагоприятные условия эксплуатации для каждого звена были выявлены нами при решении задачи в п. 2.1. Там на основании таблицы вероятностей безотказной работы блоков было установлено, что p1,min = 0.2, p2,min = 0.4, p3,min = 0.4, p4,min = 0.7. Это наименьшие вероятности безотказной работы блоков в соответствующих звеньях. Следовательно наибольшие вероятности отказа для блоков звеньев будут равны p1 = 0.8, p2 = 0.6, p3 = 0.6, p4 = 0.3. Принимая во внимание эти вероятности отказа , проведем расчет ио формуле Бернулли для каждого звена.
Звено 1. n1 = 6, p1 = 0.8,:
Р6(0) = 1 ∙ 0.80 ∙ 0.26 = 0.000064; |
|
Р6(1) = 6 ∙ 0.81 ∙ 0.25 = 0.002; |
|
Р6(2) = 15 ∙ 0.82 ∙ 0.24 = 0.015; |
|
Р6(3) = 20 ∙ 0.83 ∙ 0.23 = 0.082; |
|
Р6(4) = 15 ∙ 0.84 ∙ 0.22 = 0.246; |
|
Р6(5) = 6 ∙ 0.85 ∙ 0.21 = 0.393; |
|
Р6(6)= 1 ∙ 0.86 ∙ 0.20 = 0.262. |
|
Звено 2 и 3. n2 = n3 = 3, p2 = p3 = 0.6:
Р3(0) = 1 ∙ 0.60 ∙ 0.43 = 0.064; |
|
Р3(1) = 3 ∙ 0.61 ∙ 0.42 = 0.288; |
|
Р3(2) = 3 ∙ 0.62 ∙ 0.41 = 0.432; |
|
Р3(3) = 1 ∙ 0.63 ∙ 0.40 = 0.216; |
|
Звено 4. n4 = 1, p4 = 0.3:
Р1(0) = 1 ∙ 0.30 ∙ 0.71 = 0.700; |
|
Р1(1) = 1 ∙ 0.31 ∙ 0.70 = 0.300; |
|
2.10. Определение числа резервных блоков.
Для определения числа резервных блоков для каждого звена с целью замены блоков, вышедших из строя во время эксплуатации будем исходить также из самых неблагоприятных условий эксплуатации, как и в предыдущем пункте. Ответ на поставленный вопрос можно получить по разному. Можно принять за число резервных блоков то, которое в п.2.9 соответствует максимальному значению вероятности отказа. Такое значение дискретной случайной величины называют модой распределения. Однако лучше ориентироваться на математическое ожидание числа отказавших блоков. Поскольку здесь число отказавших блоков есть случайная величина с биномиальным законом распределения, то для такой величины математическое ожидание определяется по формуле
M = n ∙ p. |
(2.9) |
Тогда получим для каждого звена
M1 = 6 ∙ 0.8 = 4.8; |
|
M2 = 3 ∙ 0.6 = 1.8; |
|
M3 = 3 ∙ 0.6 = 1.8; |
|
M4 = 1 ∙ 0.3 = 0.3. |
|
Округляя полученные значения в большую сторону до ближайшего целого числа, приходим к выводу , что для звена № 1 следует иметь 5 запасных блоков, для звеньев №№ 2,3 по 2 блока и для звена № 4 всего 1 блок.
2.11. Определение числовых характеристик сигналов X3 и X4.
Здесь нужно определить числовые характеристики сигналов X3 и X4 по заданным числовым характеристиках входных сигналов X1 и X2. К таким числовым характеристикам относят математическое ожидание (это среднее значение случайной величины), дисперсию и среднее квадратическое или иначе стандартное отклонение (это характеристики рассеивания или разброса возможных значений случайной величины относительно математического ожидания). При этом среднее квадратическое отклонение равно арифметическому значению корня квадратного из дисперсии. В рассматриваемом варианте входные сигналы имеют нормальные законы распределения с параметрами:
M(X1) = 15.5; σ(X1) = 3.1; M(X2) = 21.0; σ(X2) = 4.2.
Но X3 = X1 + X2 и X4 = а ∙ X3.
Тогда в соответствии с теоремами о математических ожиданиях
M(X3) = M(X1) + M(X2) = 15.5 + 21.0 = 36.5 и
M(X4) = а ∙ M(X3) = 28.0 ∙ 36.5 = 1022.
В соответствии с теоремами о дисперсиях дисперсия суммы независимых случайных величин равна сумме дисперсий этих величин, т.е.
D(X3) = D(X1) + D(X2),
а дисперсия произведения постоянной на случайную величину равна квадрату постоянной, умноженной на дисперсию случайной величины, т.е.
D(X4) = а2 ∙ D(X3).
Поскольку D(X1) = σ2(X1) и D(X2) = σ2(X2), то имеем
D(X3) = 9.61 + 17.64 = 27.25;
D(X4) = 282 ∙ 27.25 = 21364;
σ(X3) = √[27.25] = 5.22;
σ(X4) = √[2136.4] = 146.16.
Дополнение
В исходных данных различных вариантов курсовой работы помимо нормальных законов распределения входных сигналов X1 и X2 имеют место также равномерные и показательные законы распределения. Если законы равномерные, то в соответствии с особенностями этих законов математические ожидания и дисперсии входных сигналов X1 и X2 определяются по формулам
M(X1) = (А1 + В1) / 2; D(X1) = (А1 − В1)2 / 12;
M(X2) = (А2 + В2) / 2; D(X2) = (А2 − В2)2 / 12,
где А1, В1, А2, В2 − левые и правые границы интервалов, в которых заключены возможные значения входных сигналов (их численные значения были заданы выше).
Если законы распределения входных сигналов показательные, то математические ожидания и дисперсии равны
M(X1) = 1 / λ1; D(X1) = 1 / λ12;
M(X2) = 1 / λ2; D(X2) = 1 / λ22,
где λ1 и λ2 − параметры этих законов.
Формулы для последующего определения числовых характеристик сигналов X3 и X4 в случае, когда законы сигналов на входе равномерные или показательные, остаются, естественно, без изменений, то есть теми, которые были использованы выше.
2.12. Определение законов распределения сигналов X3 и X4.
Для получения законов распределения сигналов X3 и X4 по известным законам распределения входных сигналов X1 и X2 необходимо более подробно рассмотреть теоретическое обоснование данной задачи, а затем привести конкрегные примеры не только для случая нормальных законов входных сигналов, но и для равномерных и показательных законов.
2. 12.1. Теоретическое обоснование.
Если случайная величина Z является суммой двух других независимых между собой случайных величин, т.е. Z = X + Y и при этом законы распределения X и Y известны, то закон распределения величины Z называют композицией (сверткой) законов распределения величин X и Y. При этом плотность распределения случайной величины Z находят по формуле
|
f (z) = |
∞ |
f (x) ∙ f (z − x) dx. |
|
(2.10) |
∫ |
|||||
−∞ |
где пределы интегрирования −∞ и ∞ в конкретной задаче композиции законов распределения определяются, исходя из особенностей этой задачи и свойств законов распределения случайных величин X и Y. Таким образом композицией законов распределения в теории вероятностей называют закон распределения суммы двух независимых случайных величин. В настоящем пункте вероятностного анализа требуется определить плотности распределения сигналов X3 и X4, т.е. f (х3) и f (х4); Поскольку
X3 = X1 + X2 |
(2.11) |
и в соответствии с заданием сигналы X1 и X2 считаются между собой независимыми, то, как следует из сказанного выше, закон распределения X3 может быть найден как композиция законов f (х1) и f (х2) по формуле
f (х3) = ∫ f (х1) ∙ f (х3 − х1) dх1. |
(2.12) |
в которой умышленно пока не записаны нижний и верхний пределы определенного интеграла. Что касается закона распределения сигнала X4, то следует иметь в виду следующее замечание:
Если две случайные величины и Y связаны между собой однозначной функциональной зависимостью Y = F(X), то f (у)dy = f (x)dx. Отсюда имеем
f (у) = f (x) ∙ dх / dy. |
(2.13) |
В нашем случае X4 = а ∙ X3. Тогда f (х4) = f (х3) ∙ dх3 / dх4. Но X3 = X4 / а, и кроме того dх3 / dх4 = 1 / а. Следовательно
f (х4) = 1 / а ∙ f (х3) |
(2.14) |
При конкретной записи этого закона для удобства расчетов следует иметь в виду, что X3 = X4 / а. Тогда
f (х4) = 1 / а ∙ f (х4 / а) |
(2.15) |
После записи выражений для f (х3) и f (х4) с соответствующими численными значениями параметров в задании требуется построить графики для f (х3) и f (х4).
Рассмотрим вначале композицию равномерных законов распределения.
2.12.2.Композиция равномерных законов распределения.
Пусть имеем входные сигналы с равномерными законами распределения. Здесь удобнее взять конкретные численные значения A1, B1 и A2, B2. Пусть для сигнала X1 A1 = 1, B1 = 3, а для сигнала Х2 A2 = 2, B2 = 5. Таким образом плотности распределения сигналов X1 и Х2 имеют вид
f (х1) = 1 / 2, 1 ≤ х1 ≤ 3; f (х1) = 0, х1 < 1, х1 > 3. |
(2.16) |
f (х2) = 1 / 3, 2 ≤ х2 ≤ 5; f (х2) = 0, х2 < 2, х2 > 5. |
(2.17) |
В соответствии с формулой (2.12) запишем
f (х3) = 1 / 6 ∙ ∫ dх1 |
(2.18) |
Как и ранее пределы интегрирования здесь пока отсутствуют. Для их определения рассмотрим область интегрирования. Имея в виду, что
х2 = х3− х1 и 2 ≤ х3 − х1 ≤ 5 |
(2.19) |
Р |
построим эту область в системе координат Oх1х3 (рис.2.1). Преобразуем левую часть неравенства (2.19) в равенство: 2 = х3 − х1. Тогда, если х1 = 1, то х3 = 3, а если х1 = 3, то х3 = 5. Построим прямую, проходящую через эти точки. Уравнение этой прямой х1 = х3 − 2. Поступим также с правой частью неравенства (2.19) х3 − х1 = 5. Тогда, если х1 = 1, то х3 = 6, а если х1 = 3 , то х3 = 8. Через эти точки также проведем прямую с уравнением х1 = х3 − 5. Между построенными прямыми и вертикальными линиями х1 = 1, х1 = 3 имеет место допустимая область интегрирования. Разобьем эту область на три части. Теперь вернемся к формуле (2.18) и вычислим определенный интеграл на каждой из частей рисунка 2.1.
|
Для части I:
3 ≤ х3 ≤ 5 |
f (х3) = |
х3 − 2 |
(1/6) ∙ dx1 = (1/6) ∙ (х3 − 3); |
|
|
∫ |
|||||
1 |
Для части II:
5 ≤ х3 ≤ 6 |
f (х3) = |
3 |
(1/6) ∙ dx1 = 1/3; |
|
|
∫ |
|||||
1 |
Для части III:
3 ≤ х3 ≤ 5 |
f (х3) = |
3 |
(1/6) ∙ dx1 = (1/6) ∙ (8 − х3); |
|
|
∫ |
|||||
х3 − 5 |
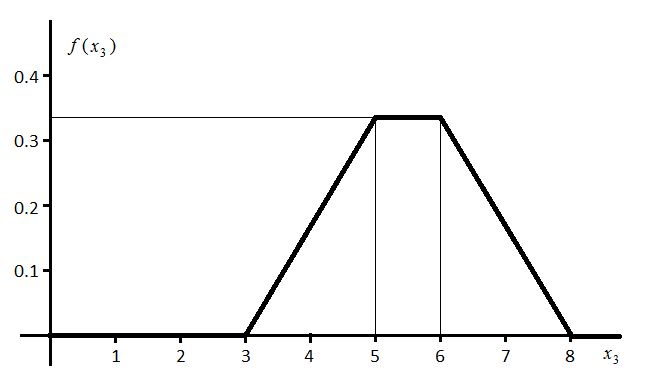
Таким образом на каждом из указанных интервалов изменения случайной величины х3 плотность распределения имеет различный вид. Мы получили здесь закон равнобедренной трапеции (см. рис. 2.2).
Рис. 2.2. Плотность распределения закона f (х3). |
Итак , закон распределения сигнала X3 f (х3) найден, построен график, иллюстрирующий этот закон. Теперь в соответствии с формулой (2.15) запишите плотность распределения f (х4) для сигнала X4. Следует иметь в виду, что линейное преобразование X4 = а ∙ X3 не изменит вид этого закона (он тоже будет законом равнобедренной трапеции), Изменятся лишь его параметры. Конкретную запись f (х4) и график f (х4) необходимо выполнить самостоятельно.
2.12.3. Композиция показательных законов распределения.
Предположим, что входные сигналы X1 и X2 имеют показательные законы распределения с параметрами λ1 и λ2, т.е.
f (х1) = λ1 ∙ exp(− λ1 ∙ х1), λ1 > 0, х1 ≥ 0; |
(2.20) |
f (х2) = λ2 ∙ exp(− λ2 ∙ х2), λ2 > 0, х2 ≥ 0; |
(2.21) |
Найдем закон распределения сигнала X3 f (х3) в этом случае. В соответствии с формулой (2.10) запишем
f (х3) = ∫ λ1 ∙ exp(− λ1 ∙ х1) ∙ λ2 ∙ exp(− λ2 ∙ (х3 − х1)) dх1 |
(2.22) |
Здесь пока не указаны пределы интегрирования. Поскольку х1 ≥ 0, то очевидно нижний предел интегрирования равен 0. Верхний предел можно найти, если считать, что х2 = х3 − х1 ≥ 0. Отсюда следует, что х3 ≥ х1. Поэтому верхний предел при интегрировании по х1 должен быть равен х3. Тогда формула (2.22) примет вид
|
f (х3) = λ1 ∙ λ2 ∙ |
х3 |
exp(− λ1 ∙ х1) ∙ λ2 ∙ exp(− λ2 ∙ (х3 − х1)) dх1 |
|
(2.23) |
∫ |
|||||
0 |
Заметим, что х3 не зависит от переменной интегрирования. Поэтому множитель под интегралом exp(− λ2 ∙ х3) можно вынести за знак интеграла. Получим после интегрирования
f (х3) = λ1 ∙ λ2 / (λ2 − λ1) ∙ [exp(− λ1 ∙ х3) − exp(− λ2 ∙ х3)] |
(2.24) |
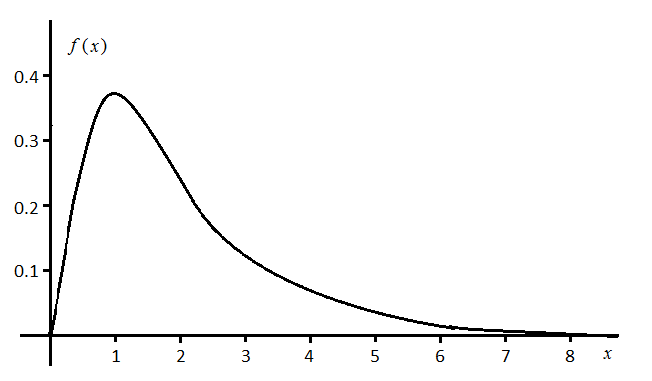
Закон распределения f (х3), определяемый формулой (2.24), в теории вероятностей называют обобщенным законом распределения Эрланга 1-го порядка. Обобщенным потому, что он справедлив при композиции показательных законов распределения с разными параметрами λ1 и λ2. Если λ1 = λ2 = λ, то закон называют законом Эрланга 1-го порядка. Он имеет вид
f (х3) = λ2 ∙ х3 ∙ exp(−λ ∙ х3) |
(2.25) |
Рис. 2.3.Плотность закона распределения Эрланга. |
Закон Эрланга 2-го порядка предполагает, что в композиции не два слагаемых, а три, 3-го порядка − четыре и т.д. График плотности распределения для закона Эрланга представлен на рис. 2.3.
Здесь также, как и ранее плотность распределения сигнала f (х4) запишется в виде
f (х4) = 1 / а ∙ f (х4 / а) |
|
Этот закон также будет законом Эрланга, но численные значения его параметров будут другими. Конкретные выражения для законов f (х3) и f (х4) с указанием численных значений параметров нужно записать самостоятельно, а также построить соответствующие графики.
2.12.4.Композиции нормальных законов распределения.
Можно показать, что композиция двух и более нормальных законов расиредслсия дает всегда нормальный закон. Говорят, что нормальный закон замкнут относительно операции свертки законов. Замкнут в том смысле, что он не допускает в пространство нормальных законов никаких других законов, кроме нормального. Для доказательства этих утверждений лучше всего использовать аппарат характеристических функций. Характеристической функцией Qх(t) случайной величины X называется математическое ожидание величины exp(i ∙ t ∙ x), где t − произвольный вещественный параметр, а i − комплексная мнимая единица. Тогда
|
Qх(t) = |
∞ |
exp(i ∙ t ∙ x) ∙ f (х) ∙ dx. |
|
(2.26) |
∫ |
|||||
−∞ |
Интеграл (2.26) носит название интеграла Фурье и выражает преобразование Фурье функции f (х). Из теории преобразования Фурье следует, что сели известна функция Qх(t) то функция f (х) может быть определена с помощью обратного преобразования Фурье, т.е.
|
f (х) =1/(2π) ∙ |
∞ |
exp(i ∙ t ∙ x) ∙ Qх(t) ∙ dt. |
|
(2.27) |
∫ |
|||||
−∞ |
Выражение (2.27) позволяет сделать вывод: плотность распределения случайной величины однозначно определяется ее характеристической функцией. Можно показать, что характеристическая функция нормального закона распределения имеет вид
Qх(t) = exp(i ∙ M(x) ∙ t − σ 2(х) ∙ t 2 / 2) |
(2.28) |
а характеристическая функция суммы двух независимых случайных величин Z = Х + Y , которые нормально распределены, записывается в виде
Qz(t) = exp(i ∙ M(z) ∙ t − σ 2(z) ∙ t 2 / 2) |
(2.29) |
где M(z) = M(x) + M(y); σ 2(z) = σ 2(x) + σ 2(y).
Выражение (2.29) свидетельствует о том, что при композиции нормальных распределений получается снова нормальное распределение с центром рассеивания M(z) = M(x) + M(y) и средним квадратическим отклонением σ(z) = √[σ 2(x) + σ 2(y)]
Исходя из изложенного, запишем выражение для плотности распределения сигнала X3
f (х3) = 1/( σ(X3) ∙ √(2π)) ∙ exp[−(х3 − M(X3))2/(2 σ 2(X3))] |
|
где M(X3) = M(X1) + M(X2), σ (X3) = √[σ 2(X1) + σ 2(X2)].
Кроме того
f (х4) = 1/( σ(X4) ∙ √(2π)) ∙ exp[−(х4 − M(X4))2/(2 σ 2(X4))] |
|
где M(X4) = а ∙ M(X3), σ (X4) = а ∙ σ (X3).
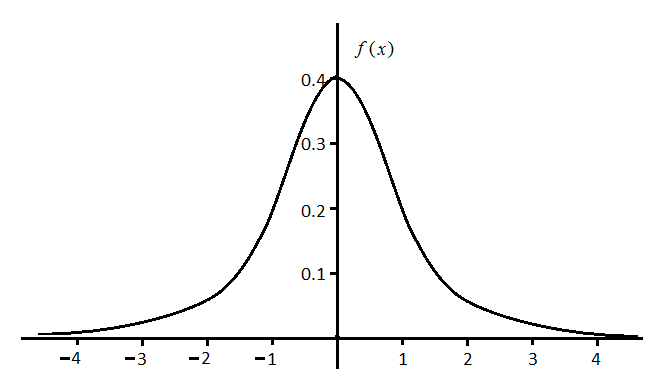
Графики для законов f (х3) и f (х4) имеют известный вид распределения Гаусса (именно так чаще называют нормальный закон). На рис.2.4.приво-дится график плотности распределения такого закона.
Рис.2.4.Плотность нормального закона распределения.
|
Как видно, это распределение строго симметрично относительно своего математического ожидания. Вам нужно в соответствии с исходными данными своего варианта записать конкретные выражения для плотностей распределения f (х3) и f (х4) с указанием численных значений параметров этих распределений и построить соответствующие графики.

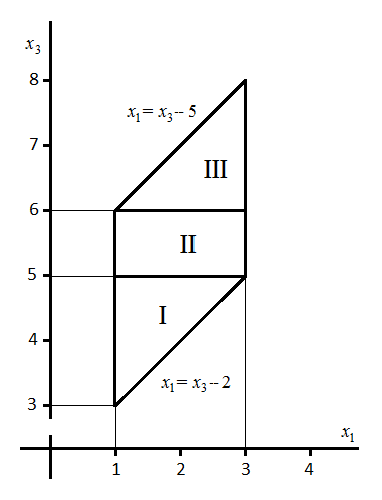 ис.
2.1. Область интегрирования.
ис.
2.1. Область интегрирования.