
РАБОТА № 3
ИССЛЕДОВАНИЕ ОБЪЕМНЫХ РЕЗОНАТОРОВ
Цель работы
Изучение характеристик объемных резонаторов и знакомство с методикой измерения их основных параметров. Исследование видов колебаний цилиндрического резонатора.
Краткие теоретические сведения
Обычный колебательный
контур, состоящий из сосредоточенных
реактивных элементов L
и C
и сопротивления
потерь
![]() ,
при переходе к сверхвысоким частотам
приобретает недостатки, которые делают
невозможным его применение. Во-первых,
уменьшение собственных реактивностей
делает их выполнение затруднительным,
во-вторых, потери энергии, обусловленные
излучением и сопротивлением поверхностного
слоя проводников, становятся чрезмерными.
,
при переходе к сверхвысоким частотам
приобретает недостатки, которые делают
невозможным его применение. Во-первых,
уменьшение собственных реактивностей
делает их выполнение затруднительным,
во-вторых, потери энергии, обусловленные
излучением и сопротивлением поверхностного
слоя проводников, становятся чрезмерными.
Это приводит к тому, что с ростом частоты добротность колебательного контура становится недопустимо низкой. По мере увеличения частоты можно осуществить переход от колебательного контура с сосредоточенными параметрами к колебательной системе с распределенными постоянными, то есть к объемному резонатору. Объемный резонатор — это некоторый диэлектрический объем, заключенный внутри проводящей металлической оболочки. Полые резонаторы можно разделить на три основные группы:
— резонаторы из отрезков длинных линий, например, коаксиальных, возбужденных на волне поперечного Т-типа;
— резонаторы из отрезков волноводов, например, прямоугольного, круглого или других сечений, возбуждаемых на видах колебаний электрического Е (ТМ) или магнитного Н (ТЕ)- типа;
— квазистационарные резонаторы, имеющие ярко выраженные области локализации электрического и магнитного полей, например, тороидальные резонаторы, резонаторы магнетронного типа.
Объемный резонатор имеет преимущества на СВЧ, так как обеспечиваются значительно меньшие потери в проводящих стенках вследствие их развитой поверхности, а также исключаются потери на излучение. Размеры резонатора оказываются соизмеримыми с рабочей длиной волны.
Так же как в контуре с сосредоточенными постоянными, в резонаторе происходит накопление энергии и колебательный процесс, в результате которого электрическая энергия преобразуется в магнитную и обратно. Однако в отличие от обычного контура в резонаторе часто трудно выделить области, в которых сосредотачивалось бы лишь электрическое или только магнитное поле, что характеризует резонатор как цепь с распределенными параметрами. Кроме того, резонатор обладает не одной, а множеством резонансных частот, каждой из которых соответствует определенный вид колебаний, отличающийся структурой электромагнитного поля в резонаторе. При достаточно большом разделении по частоте между видами колебаний свойства резонатора вблизи резонансной частоты аналогичны свойствам колебательного контура. Объемные резонаторы широко используются в приборах СВЧ, а также в схемах СВЧ в качестве фильтров, частотомеров и т.п.
Электромагнитные колебания в резонаторе, не связанном с внешними цепями, в отсутствие источников поля называются собственными или свободными. Поле собственных колебаний описывается системой однородных уравнений Максвелла, решения которых существуют при определенных частотах, называемых собственными.
Рассмотрим возможные типы свободных колебаний цилиндрического резонатора из короткозамкнутого отрезка круглого волновода.
Электрическими
(Е)
называются колебания, имеющие продольную
(направленную вдоль оси резонатора)
составляющую электрического поля —
![]() .
Колебания магнитного типа (Н)
характеризуются наличием продольной
составляющей магнитного поля
.
Колебания магнитного типа (Н)
характеризуются наличием продольной
составляющей магнитного поля
![]() .
.
Для цилиндрического
резонатора решения уравнений Максвелла
могут быть получены аналитически. С
учетом граничных условий (![]() на проводящей поверхности резонатора)
выражение для продольных составляющих
имеют вид:
на проводящей поверхности резонатора)
выражение для продольных составляющих
имеют вид:
для волн типа
![]()
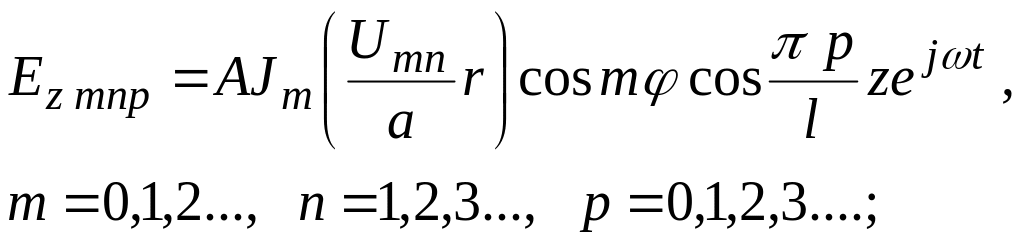
для волн типа
![]()
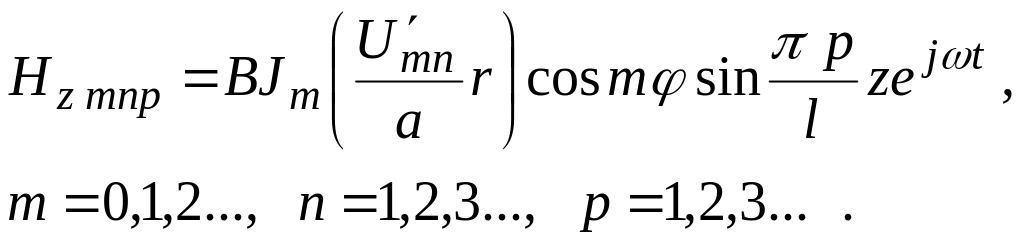 (1)
(1)
Поперечные составляющие напряженностей полей выражаются через продольные составляющие.
В выражениях (1)
![]() — амплитудные множители, зависящие от
уровня возбуждения;
— амплитудные множители, зависящие от
уровня возбуждения;
![]() – функция Бесселя 1-го рода т-го
порядка;
– функция Бесселя 1-го рода т-го
порядка;
![]() и
и
![]() –
корни функции
и ее производной
–
корни функции
и ее производной
![]() соответственно,
соответственно,
![]() — радиус и
длина резонатора,
— радиус и
длина резонатора,
![]() — цилиндрические координаты. Индексам
т,
n,
p соответствует
множество видов колебаний в резонаторе
и
,
отличающиеся структурой поля.
— цилиндрические координаты. Индексам
т,
n,
p соответствует
множество видов колебаний в резонаторе
и
,
отличающиеся структурой поля.
Как видно из (1), поле представляет собой стоячую волну, пространственное распределение которой остается неизменным, меняются только значения напряженностей поля во времени по гармоническому закону.
Индекс т определяет число периодов (или волн) поля по азимутальной координате φ, а также порядок функции Бесселя, согласно которой происходит изменение поля по радиальной координате r.
Индекс n – номер корня функции Бесселя определяет число вариаций поля по радиусу.
Индекс p показывает число полуволн поля, укладывающихся вдоль резонатора:
![]() ,
(2)
,
(2)
где
![]() —
длина волны в волноводе, из отрезка
которого образован резонатор, при
возбуждении его на резонансной частоте.
—
длина волны в волноводе, из отрезка
которого образован резонатор, при
возбуждении его на резонансной частоте.
Равенство (2) является условием резонанса и позволяет найти резонансную длину волны любого вида колебаний:
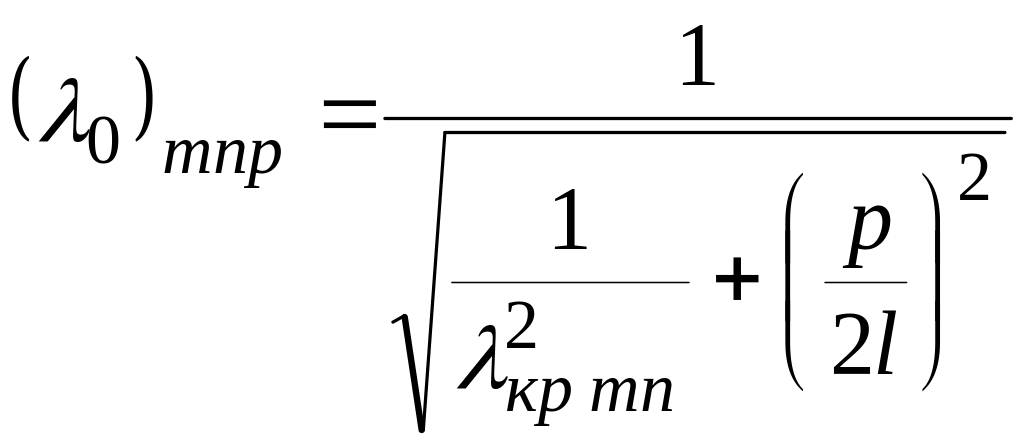 .
.
Например, для видов колебаний
![]()
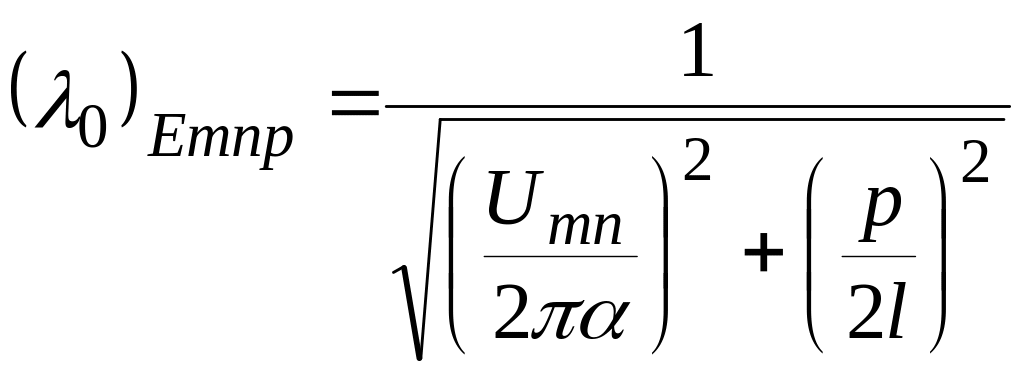 , (3)
, (3)
для
![]() видов колебаний
видов колебаний
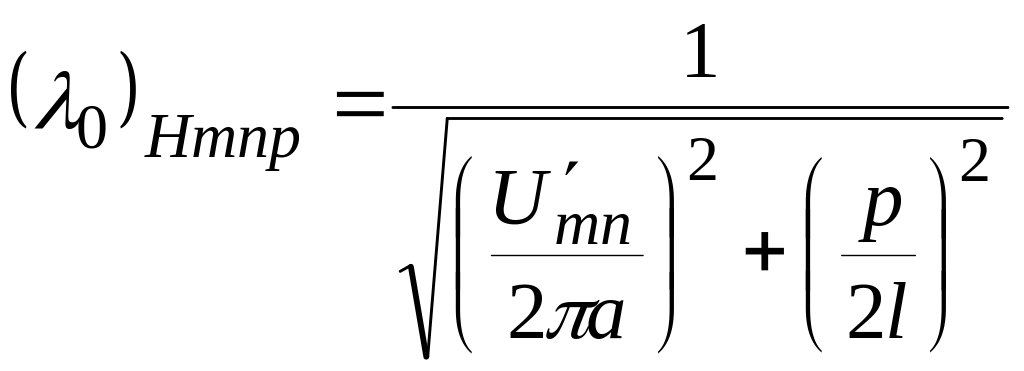 . (4)
. (4)
В таблице приведены значения первых корней функций Бесселя и их производных.
-
m
n
0
1
2,405
3,832
1
1
3,832
1,841
2
1
5,136
3,054
Вид колебаний с наибольшей собственной длиной волны (наименьшей собственной частотой) называется основным или низшим. Другие виды колебаний называются высшими.
П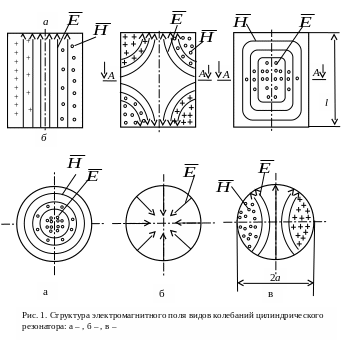 ри
достаточно большой длине цилиндрического
резонатора низшим является вид колебаний
ри
достаточно большой длине цилиндрического
резонатора низшим является вид колебаний
![]() ,
однако при
,
однако при
![]() основным является вид колебаний
основным является вид колебаний
![]() ,
резонансная длина волны которого
вычисляется по формуле
,
резонансная длина волны которого
вычисляется по формуле
![]() .
Структура электромагнитного поля в
цилиндрическом резонаторе на видах
колебаний
.
Структура электромагнитного поля в
цилиндрическом резонаторе на видах
колебаний
![]() показана на рис. 1.
показана на рис. 1.
В отличие от резонаторов, образованных из отрезков волноводов, тороидальный резонатор, изображенный на рис. 2, а, при возбуждении на низшем виде колебаний имеет области локализации электрического и магнитного полей и поэтому может быть отнесен к квазистационарным. Как видно из этого рисунка, электрическое поле в основном сосредоточено в узком зазоре между торцами внутренних цилиндров, а магнитное – в тороидальной части резонатора.
Расчет собственных частот резонаторов произвольной формы весьма сложен и может быть выполнен с достаточно высокой точностью лишь численными методами с применением ЭВМ. Для практических целей наибольший интерес представляют характеристики резонатора при возбуждении его на низшем виде колебаний. В этом случае широко используется метод эквивалентных схем, при котором резонатор представляется колебательным контуром из сосредоточенных элементов.
Роль емкости в
эквивалентной схеме (рис. 2, б) играет
зазор резонатора, индуктивности —
тороидальная часть резонатора, потери
в стенках резонатора могут быть отнесены
к некоторому сечению между точками
![]() и заменены эквивалентным сопротивлением
и заменены эквивалентным сопротивлением
![]() (или проводимостью
(или проводимостью
![]() ).
).
Выражение для приближенного расчета резонансной длины волны резонатора на низшем виде колебаний может быть получено методами электростатики и магнитостатики
![]() , (5)
, (5)
где все размеры в
сантиметрах,
![]() см/с — скорость света.
см/с — скорость света.
Колебательные
свойства объемных резонаторов на
отдельных видах колебаний характеризуются
теми же параметрами, что и свойства
контура с сосредоточенными постоянными:
собственная добротность
![]() ,
эквивалентное активное сопротивление
при резонансе
,
характеристическое сопротивление
,
эквивалентное активное сопротивление
при резонансе
,
характеристическое сопротивление
![]() .
Причем для колебательного контура эти
параметры являются производными от
исходных параметров
.
Причем для колебательного контура эти
параметры являются производными от
исходных параметров
![]() .
Для объемного резонатора исходными
являются параметры
.
Для объемного резонатора исходными
являются параметры
![]() ,
,
так как они могут быть выражены через
понятия электромагнитного поля и
непосредственно измерены. Следует,
однако, заметить, что в отличие от
добротности параметры
и
определяются неоднозначно и зависят
от места их вычисления или измерения в
резонаторе.
,
,
так как они могут быть выражены через
понятия электромагнитного поля и
непосредственно измерены. Следует,
однако, заметить, что в отличие от
добротности параметры
и
определяются неоднозначно и зависят
от места их вычисления или измерения в
резонаторе.
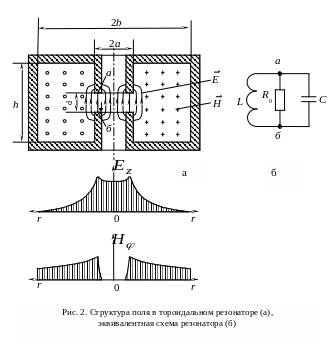
Собственная
добротность
объемного резонатора пропорциональна
отношению энергии
![]() ,
запасенной полем резонатора, к энергии
,
запасенной полем резонатора, к энергии
![]() ,
рассеиваемой в резонаторе за период
колебаний:
,
рассеиваемой в резонаторе за период
колебаний:
![]() , (6)
, (6)
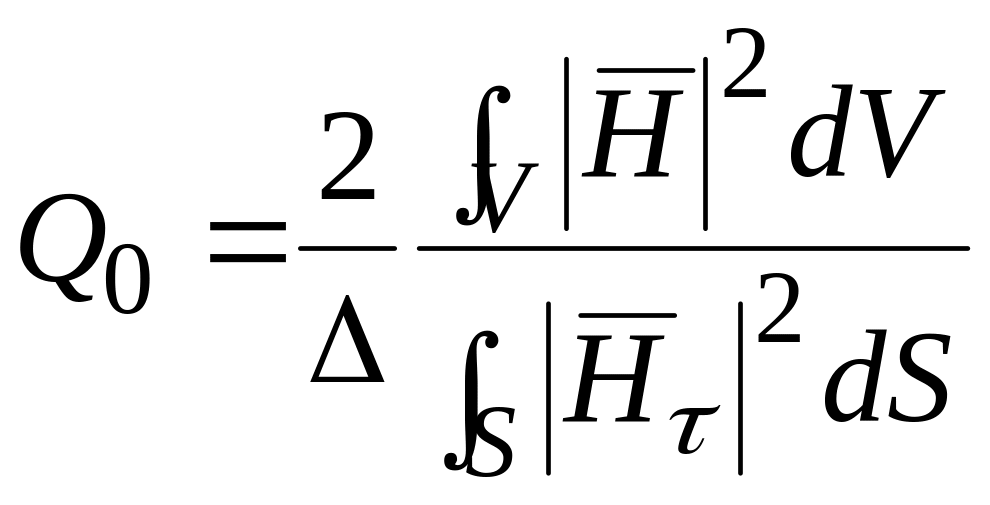 .
.
Приближенно добротность можно оценить по формуле
![]() .
(7)
.
(7)
В формулах (6), (7)
![]() — мощность потерь в резонаторе,
— мощность потерь в резонаторе,
![]() — объем и площадь внутренней поверхности
резонатора,
— объем и площадь внутренней поверхности
резонатора,
![]() — глубина проникновения поля в металл.
Для меди
— глубина проникновения поля в металл.
Для меди
![]() ,
см. Добротность реального резонатора
оказывается меньше, чем вычисленная по
(7), из-за потерь, связанных с шероховатостью
поверхности резонатора, потерь в
контактах.
,
см. Добротность реального резонатора
оказывается меньше, чем вычисленная по
(7), из-за потерь, связанных с шероховатостью
поверхности резонатора, потерь в
контактах.
Характеристическое
сопротивление
численно равно отношению
![]() .
Эквивалентное параллельное сопротивление
резонатора при резонансе
.
Эквивалентное параллельное сопротивление
резонатора при резонансе
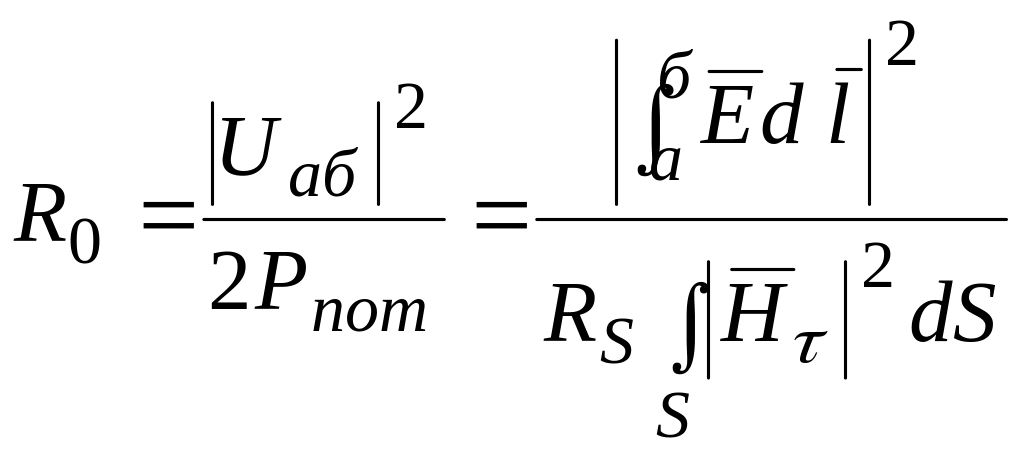 ,
(8)
,
(8)
где
![]() —
модуль напряжения между точками а
и б
резонатора,
—
модуль напряжения между точками а
и б
резонатора,
![]() —
напряженность электрического поля
вдоль линии, соединяющей точки а
и б.
—
напряженность электрического поля
вдоль линии, соединяющей точки а
и б.
Из (6) и (8) следует, что не зависит от потерь в резонаторе и является его геометрической характеристикой:
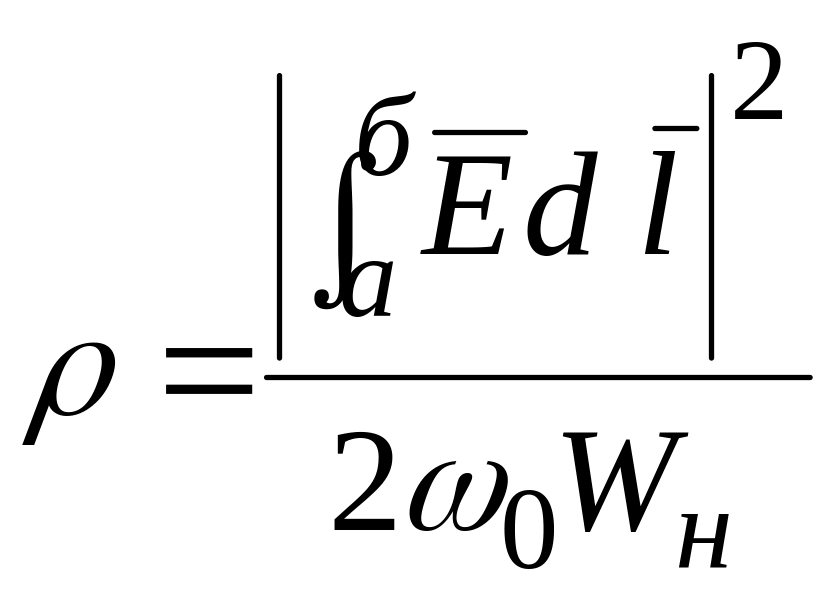 .
(9)
.
(9)
Величина
цилиндрического резонатора на виде
колебаний
,
рассчитанная вдоль его оси между
торцевыми стенками, определяется
выражением
![]() ,
Ом. В резонаторах электронных приборов
СВЧ
обычно определяется вдоль траектории
электронного потока, пронизывающего
резонатор, и характеризует величину
электрического поля в области
взаимодействия. Для тороидального
резонатора величина
может быть рассчитана приближенно по
формуле
,
Ом. В резонаторах электронных приборов
СВЧ
обычно определяется вдоль траектории
электронного потока, пронизывающего
резонатор, и характеризует величину
электрического поля в области
взаимодействия. Для тороидального
резонатора величина
может быть рассчитана приближенно по
формуле
![]() , Ом.
, Ом.
Описание экспериментальной установки и методики измерений резонансной частоты, добротности и характеристического сопротивления резонаторов
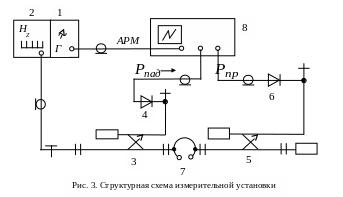
Структурная схема измерительной установки показана на рис. 3. Схема состоит из панорамного измерителя КСВ типа Р2-59, который включает блок генератора СВЧ 1, работающий в режиме “качания” частоты, цифровой индикатор частоты 2, направленный ответвитель 3 с детектором 4, выделяющий сигнал, пропорциональный падающей мощности, направленный ответвитель 5 с детектором 6, выделяющий сигнал, пропорциональный проходящей через исследуемый резонатор 7 мощности, блок индикатора 8, на экране которого наблюдается зависимость проходящей мощности от частоты, систему АРМ, обеспечивающую постоянство выходной мощности генератора в рабочем диапазоне частот.
Д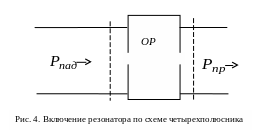
 ля
экспериментального исследования
резонаторы (цилиндрический или
тороидальный) включают в волноводный
тракт по схеме четырехполюсника, т.е.
“на проход” (рис. 4). Связь резонаторов
с волноводным трактом осуществляется
через щели в боковых стенках. Диапазон
качания частоты генератора выбирается
так, чтобы резонансная частота резонатора
оказалась примерно в его середине. При
этом на экране индикаторного устройства
появляется резонансная кривая,
отображающая зависимость проходящей
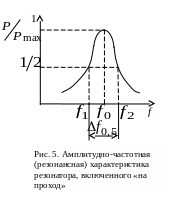
мощности от частоты (рис. 5). Совмещая
частотную метку с вершиной резонансной
кривой, можно измерить резонансную
частоту резонатора
ля
экспериментального исследования
резонаторы (цилиндрический или
тороидальный) включают в волноводный
тракт по схеме четырехполюсника, т.е.
“на проход” (рис. 4). Связь резонаторов
с волноводным трактом осуществляется
через щели в боковых стенках. Диапазон
качания частоты генератора выбирается
так, чтобы резонансная частота резонатора
оказалась примерно в его середине. При
этом на экране индикаторного устройства
появляется резонансная кривая,
отображающая зависимость проходящей
мощности от частоты (рис. 5). Совмещая
частотную метку с вершиной резонансной
кривой, можно измерить резонансную
частоту резонатора
![]() на данном виде колебаний.
на данном виде колебаний.
Добротность
резонатора определяется по ширине
резонансной кривой проходящей мощности.
При этом измеряется нагруженная
добротность
![]() ,
которая отличается от собственной
добротности ненагруженного резонатора
из-за потерь мощности во внешних цепях
,
которая отличается от собственной
добротности ненагруженного резонатора
из-за потерь мощности во внешних цепях
![]() .
.
Однако при слабой
связи резонатора с внешними цепями
![]() и величина нагруженной добротности
стремится к собственной. Измерив по
резонансной кривой с помощью частотной
метки частоты
и величина нагруженной добротности
стремится к собственной. Измерив по
резонансной кривой с помощью частотной
метки частоты
![]() ,
соответствующие половинному уровню
проходящей мощности, можно вычислить
добротность резонатора по известному
соотношению
,
соответствующие половинному уровню
проходящей мощности, можно вычислить
добротность резонатора по известному
соотношению
![]() ,
,
где
![]() — полоса пропускания по уровню половинной
мощности.
— полоса пропускания по уровню половинной
мощности.
Для измерения волнового сопротивления обычно используется метод малых возмущений. Суть его состоит в том, что при введении в объемный резонатор малых возмущающих тел собственная частота резонатора изменяется на некоторую величину. Связь между относительным изменением собственной частоты резонатора и параметрами возмущающего тела устанавливается с помощью теоремы возмущений Слэтера:
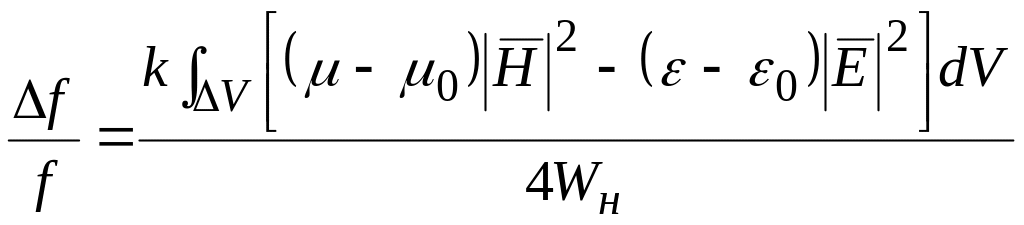 , (11)
, (11)
где
![]() —
напряженности электрического и магнитного
полей в месте расположения возмущающего
тела,
—
напряженности электрического и магнитного
полей в месте расположения возмущающего
тела,
![]() —
объем возмущающего тела,
—
объем возмущающего тела,
![]() —
изменение резонансной частоты, f
— частота при
введении возмущающего тела, k
— коэффициент, зависящий от формы,
материала возмущающего тела,
—
изменение резонансной частоты, f
— частота при
введении возмущающего тела, k
— коэффициент, зависящий от формы,
материала возмущающего тела,
![]() — диэлектрическая и магнитная
проницаемости материала возмущающего
тела и вакуума соответственно.
— диэлектрическая и магнитная
проницаемости материала возмущающего
тела и вакуума соответственно.
Из определения
характеристического сопротивления (9)
следует, что если электрическое поле в
области, где проводится измерение,
однородно, то
пропорционально отношению
![]() ,
а из (11) следует, что если в месте
расположения тела магнитное поле равно
нулю, то смещение резонансной частоты
,
а из (11) следует, что если в месте
расположения тела магнитное поле равно
нулю, то смещение резонансной частоты
![]() также пропорционально
.
Следовательно,
оказывается пропорционально величине
,
которая может быть измерена экспериментально.
также пропорционально
.
Следовательно,
оказывается пропорционально величине
,
которая может быть измерена экспериментально.
Постоянную k в (11) можно положить равной 1, если при , стремящимся к нулю, поле в резонаторе практически не отличается от невозмущенного. Для тороидального резонатора этому условию удовлетворяет тонкая диэлектрическая пленка, расположенная по внутреннему краю зазора резонатора. На практике удобнее воспользоваться диэлектрическим стержнем, размещая его на оси резонатора. В этом случае волновое сопротивление определяется по формуле
![]() ,
(12)
,
(12)
где d — ширина зазора, мм;
S — площадь поперечного сечения стержня, мм2;
![]() ,
МГц;
,
МГц;
f, ГГц;
![]() —
относительная
диэлектрическая проницаемость
диэлектрика;
—
относительная
диэлектрическая проницаемость
диэлектрика;
![]() — коэффициент,
учитывающий отличие поля у края зазора
и на оси резонатора;
— коэффициент,
учитывающий отличие поля у края зазора
и на оси резонатора;
, Ом.
При измерениях используют также возмущающие тела в виде тонких металлических и диэлектрических стержней, шариков, дисков. Явление смещения частоты при введении в резонатор малых возмущающих тел используется также для определения структуры электромагнитного поля в резонаторе при идентификации видов колебаний.
