1.4. Кінематичні ланцюги

Кінематичним ланцюгом називають зв'язану систему ланок, які входять у кінематичні пари. Кінематичні ланцюги поділяють на прості та складні, замкнуті та незамкнуті.

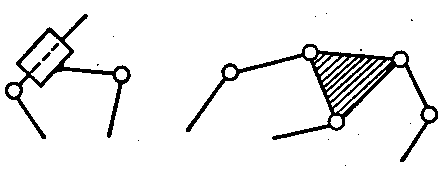
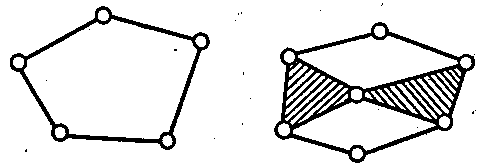
Простим навивають такий кінематичний ланцюг, у якого кожна ланка вхсідить не більше як до двох кінематичних пар (рис Л .13,а,в складним - у якого е хоч одна ланка, яка входить більше, ні* до двох кінематичних пар ( рис.1.13,6,г).

Незамкнутим називають такий кінематичний ланцюг, у якого є ланки, які входять до однієї кінематичної пари (рис.І.ІЗ,а,б); замкнутим - у якого кожна ланка входить уе менше як до двох кі­нематичних пар (рис. І. ІЗ, в, г).

Кінематичні ланцюги, як і механізми, поділяють иа плоскі те просторові. Просторові незамкнуті кінематичні ланцюги використо­вуються в механізмах маніпуляторів. Маніпулятором називається технічний пристрій, призначений для відтворення робочих функцій рухи людини. Приклад такого механізму показаний на рис.1.14.

а б

в г

Рис. 1.13. Схема кінематичних ланцюгів:

а – простий незамкнутий; б – складний незамкнутий;

в – простий замкнутий; г – складний замкнутий

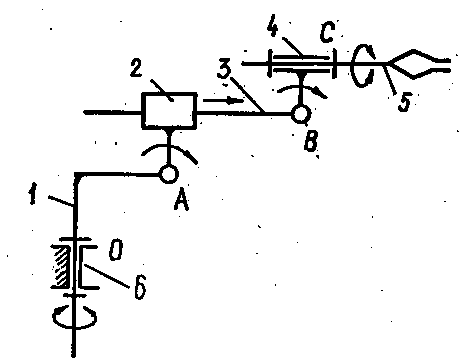
Рис.1.14. Схема механізму маніпулятора

У машинобудуванні використовуються переважно замкнуті кінематичні ланцюги. Ножний механізм являє собою деякий кінематичний ланцюг з однією нерухомою ланкою. Тому можна дати таке визначення механізму.

Механізм - це кінематичний ланцюг з однією нерухомою ланкою, у якого при заданому русі однієї або кількох ланок всі інші лан­ки виконують цілком визначені рухи.

1.5. Число ступенів вільності .Механізму

Ступенем вільності механізму (або числом ступенів вільності) називається число незалежних примусових рухів, які треба задати ланкам механізму, щоб забезпечити цілком визначені ( узгоджені) рухи всіх інших ланок.

Для визначення числа ступенів вільності будь-якого механіз­му необхідно підрахувати число ступенів вільності всіх рухомих ланок, вважаючи їх вільними тілами, не зв'язаними між собою кінематичними парами, а потім від цього числа слід відняти число умов зв’язку, які накладаються на ланки кінематичними парами.

Виведемо формулу для визначення числа ступенів вільності плоского механізму. Нехай плоский механізм складається з ланок, одна з яких є нерухомою. Тому кількість рухомих ланок складає n-1. Кожна вільна ланка в площині має три ступені вільності. Якщо б ланки механізму не були зв’зязані між собою,.то загальна кількість простих рухів усіх рухомих ланок складала . Але ж ланки механізму не с вільними тілами, вони зв’язані між собою кінематичними парами. Кожна пара 1-го роду зменшує загальну кількість рухів на 2, а кожна пара 2-го роду - на 1. Якщо ж механізм має всього p₁, пар 1-го роду та р₂ пар 2-го роду, то загальна кількість втрачених рухів буде складати 2p₁-1p₂. Віднявши втрачені ланками рухи від їхньої загальної кількості, одержимо число W ступенів вільності механізму:

1.1

Рівність (1.1) називається формулою П.Л.Чебишева ( І82І-І894).

Аналогічно можна одержати формулу для визначення числа ступенів вільності просторового механізму. Вона матиме вигляд:

1.2

де p₁,p₂,p₃,p₄,p₅ - число кінематичних пар відповідно 1-го,2-го,3-го,4-го та 5-го родів.

Рівняння ( 1.2) називається формулою А.П.Малишева (І879-І962 ).

Число ступенів вільності плоского механізму на практиці визначає кількість початкових ланок.

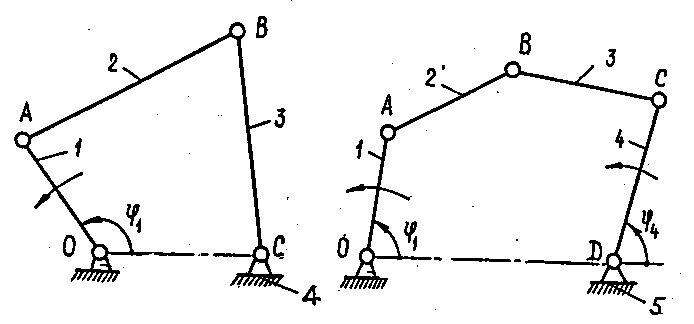
Початковою називається ланка, якій задасть закон руху при дослідженні механізму. Так, наприклад, для плоского шарнірного чотириланкового механізму, показаного на рис.1.15,а, число ступенів Вільності .

а б

Рис.1.15. Визначення ступенів вільності шарнірних механізмів:

а – чотири ланковий механізм (W=1); б – п’ятиланковий механізм (W=2)

Отже, механізм має одну початкову ланку, тобто досить зада­ти закон руху одній ланці щоб визначити рух усіх інших ланок. Якщо, наприклад, ланці І надати обертального руху, тоді ланки 2 і 3 будуть мати також цілком визначені рухи. Положення ланки І можна задати кутом повороту φ₁ , Ця кутова координата визначить положення і інших ланок ( 2 та 3). Тому її називають узагальненою координатою.

Для механізму, схема якого показана на рис.1.15,б, число ступенів вільності

Якщо у цьому механізмі задати положення лише ланки 1, то положення решти рухомих ланок буде невизначеним. Коли ж задати ще положення іншої ланки, наприклад, ланки 4 (кутом повороту φ) то всі інші ланки механізму будуть займати цілком визначене положення. Отже, механізм має дві початкові ланки, і положення всіх його ланок визначається двома узагальненими координатами.

Початкові ланки можуть збігатися із вхідними ланками механіз­му, а можуть і не збігатися. Добір початкової ланки зумовлюється зручністю визначення положень ланок механізму і зручністю аналізу його руху. Якщо у механізмі за початкову приймається ланка, яка виконує зворотно-поступальний рух, то узагальненою координатою буде її лінійна координата. На сxемах механізмів початкові ланки позначають круговими або прямими стрілками.

При дослідженні рухомості плоских механізмів можуть виявитися такі ланки, які вносять у механізм або зайві ступені вільності, або зайві умови зв’язку (зайві в’язі). Такі ланки називають пасивними. Так, наприклад, плоский кулачковий механізм (рис.1.16), який використовується в двигунах внутрішнього згоряння, має чотири ланки; кулачок 1, ролик 2, штовхач 3 та стояк 4. Ланки 1 та 4, 2. та 3 утворюють обертальні кінематичні пари 0 та В , ланки 3 та 4 - поступальну кінематичну пару, а ланки 1 та 2 - пару 2-го , роду. Число ступенів вільності

В той же час положення веденої ланки (штовхача 3) залежить лише від положення ведучої ланки (кулачка І). Пояснюється це тим що ролик 2 мас круглу форму і того центр обертання збігається з геометричним центром. Тому ролик може вільно обертатися навколо своєї осі, не впливаючи на характер руху всього механізму. Можливість обертання ролика є зайвим ступенем вільності, а ролик є пасивною ланкою. Він являє собою конструктивний елемент, який введено для зменшення опору сил тертя і спрацювання ланок.

Схему механізму шарнырного паралелограма, у якого зображено на рис.1.17. У механізмі паралелограма обидва кривошипи (ланки 1 та 3) обертаються в одному напрямі з однаковими кутовими швид-

костями а шатун 2 рухається поступально. Коли механізм

прийде в крайнє положення (рис.1.17,б) і всі ланки розташо-

вуються на одній прямій, то подальший рух стає не визначеним.

Механізм може або продовжувати рух як паралелограм, або точ-

Рис.1.16. Схема кулачкового механізму із зайвим ступенем вільності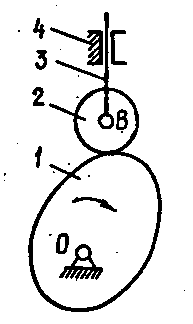

ка В може змінити напрям свого руху (рис.І.17,в) і механізм

перетвориться в

Рис.1.17. Схема механізму паралелограма

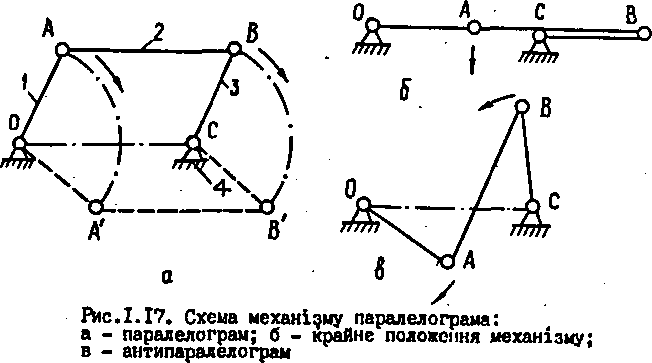
а – паралелограм; б – крайнє положення механізму; в – анти паралелограм

антипаралелограм. Щоб забезпечити визначеність руху, використовують механізм подвійного паралелограма (рис.1.18); у якого . Механізм як і раніше буде мати один ступінь вільності, хоч у відповідності з формулою (1.1) одержимо:

Рис.1.18. Схема механізму подвійного паралелограма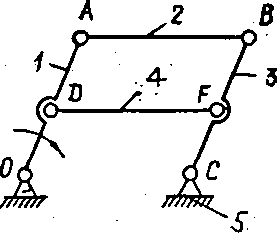

Такий результат обумовлений тим, що додаткова ланка 4 є пасивною. Утворюючи пари 1-го роду з ланками 1 та 3, вона вносить один зайвий (пасивний ) зв’язок (q = 1), який не враховано в формулі (1.1). • З урахуванням пасивного зв’язку (пасивні в’язі ) матимемо

що й відповідає дійсності. Якщо ж в механізм паралелограма ввести додаткову ланку 4, довжина якої (рис.1.19), то утворений кінематичний ланцюг дійсно матиме W = 0.

Рис.1.19. Кінематичний ланцюг з нульовим ступенем вільності

Деякі механізми мажуть мати дві і більше пасивних ланок. їх вводять у механізм для забезпечення визначеності руху, підвищення жорсткості системи, зменшення впливу деформацій на рух механізму, більш рівномірного розподілення сил, які діють на ланки механізму, зменшення сил тертя тощо.