
- •1. Структурний аналіз механізмів
- •1.1. Основні поняття та визначення
- •1.2. Класифікація кінематичних пар
- •1.4. Кінематичні ланцюги
- •1.5. Число ступенів вільності .Механізму
- •1.6. Пасивні в’язі. Раціональні механізми
- •1.7. Структура плоских важільних механізмів
- •1.8. Синтез чотириланкових важільних механізмів
- •1.9. Заміна у плоских механізмах вищих пар нижчими
- •2. Кінематичне дослідження плоских важільних механізмів
- •2.1. Задачі та методи кінематичного дослідження механізмів.
- •2.2. Побудова планів механізму і траєкторій окремих точок
- •2.3. Основні рівняння для швидкостей і прискорень
- •2.4. Теореми подібності для швидкостей та прискорень
- •2.5. Побудова планів швидкостей і прискорень механізму
- •2.6. Побудова планів швидкостей і прискорень шарнірного чотири ланкового механізму: а – план механізму; б – план швидкостей; в – план прискорень
- •2.6. Визначення радіуса кривизни траєкторії
- •2.7. Дослідження механізмів методом кінематичних діаграм
- •2.8. Аналітичний метод кінематики
- •3. Зубчасті механізми
- •3.1. Загальні відомості про зубчасті механізми
- •3.3 Евольвента кола, її рівняння і властивості
- •3.5. Елементи та властивості евольвентного зачеплення
- •3.6. Евольвента зубчаста передача
3.3 Евольвента кола, її рівняння і властивості
Евольвентою кола називається крива, яка описує будь-яка точка кривої при її перекочуванні без ковзання по цьому колу. Коло, по якому перекочується пряма, називається основним, а пряма – твірною прямою.
На
рис.3.10 зображені основне коло радіуса
rb
і твірна пряма n-n,
яка в початковому положенні показана
штрихами. При перекочуванні твірної
прямої по основному колу в одному
напрямку точка К
прямої описує праву гілку евольвенти
Рис.3.10.
Утворення евольвенти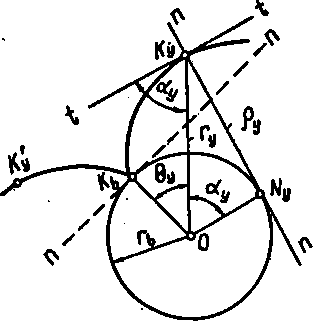 KbKy,
а при перекочуванні твірної прямої у
протилежному напрямку – ліву гілку
евольвенти
KbKy,
а при перекочуванні твірної прямої у
протилежному напрямку – ліву гілку
евольвенти
![]() .
.
![]() .
.
Кут
ϴу,
утворений початковим радіусом-вектором
евольвенти OKb
і її поточним радіусом-вектором ОКу,
називається евольвентним-кутом,
або інволютою кута αу,
тобто
![]() .
.
Положення будь-якої точки евольвенти цілком визначається двома параметрами: радіусом-вектором ry і евольвентним кутом ϴу.
В
зв’язку
з тим, що пряма n-n
перекочується по основному колу без
ковзання, можна скласти рівність
![]() .
Підставивши значення дуги і відрізка,
будемо мати
.
Підставивши значення дуги і відрізка,
будемо мати
![]() ,
,
звідки
![]() .
(3.5)
.
(3.5)
Зв’язок між радіусом-вектором ry і кутом αу встановлюється із трикутника KyONy залежністю.
![]() .
(3.6)
.
(3.6)
Формули (3.5) і (3.6) виражають рівняння евольвенти в параметричній формі.
Для геометричної теорії зачеплення важливе значення мають такі основні властивості евольвенти:
евольвента – симетрична крива, що має дві гілки, які сходяться в точці Кb на основному колі; отже, евольвента не має точок всередині основного кола;
точка Ny є миттєвий центр обертання прямої п-п і центр кривизни евольвенти в точці Ку; тому нормаллю до евольвенти в будь-якій її точці є пряма, дотична до основного кола;
відрізок Ку Ny є радіус кривизни евольвенти в точці Ку;
кут профілю αу і радіус кривизни ρу в початковій точці евольвенти (Кb) дорівнюють, нулю; при віддаленні точок евольвенти від основного кола кут профілю αу і радіус кривизни ρу збільшуються;
при збільшенні радіуса основного кола кривизна евольвентного профілю поступово зменшується і при rb=∞ евольвента перетворюється у пряму лінію.
3.4. Параметри евольвентного циліндричного нормального зубчастого колеса
Параметрами зубчатого колеса називаються розрахункові величини, які визначають основні розміри колеса. Ці параметри розглядають в будь-якому перерізі колеса площиною, перпендикулярною до його осі, тобто в торцевому перерізі. Розглянемо параметри циліндричного прямозубого зубчастого колеса.
В торцевому перерізі колеса (рис.3.11) коло западин діаметра df обмежує зуб’ї з боку тіла колеса, а з другого боку зуб’ї обмежені колом вершин діаметра da. Відстань між колами вершин і западин визначає висоту зуба h. Евольвентний профіль зуба відповідає цілком визначеному основному колу діаметра db. Крім перелічених кіл на рис.3.11 показане так зване ділильне коло діаметром d.
Ділильним
називається таке коло, яке перетинає
боковий евольвентний профіль зуба в
точці, для якої кут профілю
![]() .
У відповідності з рівнянням (3.6)
одержуємо таку залежність між діаметрами
ділильного та основного кіл:
.
У відповідності з рівнянням (3.6)
одержуємо таку залежність між діаметрами
ділильного та основного кіл:
![]() .
(3.7)
.
(3.7)

Рис.3.11. Параметри евольвентного циліндричного
нормального зубчастого колеса
Якщо довжина кола – ділильного, основного – поділити на число зуб’їв колеса, то одержимо довжини дуг між однойменними профілями двох сусідніх зуб’їв, які називаються відповідно кроком р по ділильному колу і кроком pb по основному колу.
Отже,
кроком зубчастого колеса називається
відстань між однойменними точками двох
сусідніх зуб’їв,
виміряна по дузі відповідного кола.
Дуги р
і pb
відповідають одному і тому ж кутовому
кроку
![]() .
Звідси випливає, що кроки пропорційні
радіусам відповідних кіл. Кутовий крок
можна також визначити із співвідношення
.
Звідси випливає, що кроки пропорційні
радіусам відповідних кіл. Кутовий крок
можна також визначити із співвідношення
![]() ,
,
де Z – число зуб’їв зубчастого колеса.
Важливим параметром зубчастого колеса є крок р по ділильному колу. Очевидно, що крок р, помножений на число зуб’їв Z визначає довжину ділильного кола:
![]() ,
,
звідки
![]() .
(3.8)
.
(3.8)
Величина m, що являє собою відношення кроку р до числа π, називається модулем зубчастого колеса. Модуль вимірюється в міліметрах. Значення модуля залежить від того, по якому колу він вимірюється. Значення модуля по ділильному колу стандартизовані.
Стандартом встановлені два ряди модулів. У першому ряду, якому слід віддавати перевагу, передбачені такі модулі в міліметрах: 0,05; 0,06; 0,08; 0,1; 0,12; 0,15; 0,2; 0,25; 0,3; 0,4; 0,5; 0,6; 0,8; 1,0; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25; 32; 40; 50; 60; 80; 100.
У другому ряду передбачені модулі, проміжні між модулями першого ряду, наприклад: 0,07; 0,09; 3,5; 4,5; 7; 9; 11 та інші.
За допомогою модуля по ділильному колу визначаються усі розміри зубчастого колеса. Так, наприклад, на основі рівностей (3.7) і (3.8) матиме таку формулу для діаметра основного кола:
![]() .
(3.9)
.
(3.9)
Із співвідношення (3.8) одержуємо таку формулу для визначення кроку колеса по ділильному колу:
![]() .
.
Оскільки кроки пропорційні відповідним радіусам, то крок по основному колу
![]() .
.
Зазначимо, що крок по ділильному колу дорівнює сумі товщини зуба S і ширині западини е по цьому колу:
![]() .
.
Залежно від товщини зуба по ділильному колу розрізняють три види зубчастих коліс:
колеса нормальні, або нульові, у яких товщина зуба дорівнює ширині западини:
![]() ;
;
колеса додатні, у яких товщина зуба більша ширини западини:
![]() ,
тобто
,
тобто
![]() ;
;
колеса від’ємні, у яких товщина зуба менша ширини западини:
![]() ,
тобто
,
тобто
![]() .
.
Зубчаста
передача, утворена двома нормальними
зубчастими колесами, називається
нормальною,
або нульовою.
У коліс нормальної передачі початкові
кола, які в процесі передачі руху
перекочуються одне по одному без
ковзання, збігаються з ділильними. Тому
діаметри цих кіл однакові, тобто
![]() ,
,
![]() .
.
Зубчасті
колеса додатні та від’ємні називаються
коригованими,
або колесами
зі
зміщенням,
а передача, у складі якої є кориговане
колесо, називається коригованою,
або передачею
зі зміщення.
У коліс коригованої передачі початкові
кола можуть не збігатися з ділильником.
У такому випадку
![]() ;
;
![]() .
Діаметр початкового кола можна визначити
із рівняння (3.6):
.
Діаметр початкового кола можна визначити
із рівняння (3.6):
![]() ,
,
де αW – кут профілю для точки евольвенти, розташованої на початковому колі.
Крок колеса по початковому колу pW називається кроком зачеплення. Між кроком зачеплення pW і основним кроком pb матиме залежність
![]() .
.
Початкові
кола коліс ділять зуб’ї на дві частини:
голівку
зуба
висотою ha,
і ніжку
зуба
висотою hf.
Для нормальних коліс звичайно приймають
![]() і
і
![]() .
Отже, висота ніжки зуба більша за висоту
голівки зуба. Тому у зубчастій передачі
між колом вершин одного колеса і колом
западин другого колеса існує радіальний
зазор
.
Отже, висота ніжки зуба більша за висоту
голівки зуба. Тому у зубчастій передачі
між колом вершин одного колеса і колом
западин другого колеса існує радіальний
зазор
![]() ,
який забезпечує нормальну роботу
передачі. Із наведених співвідношень
випливає, що висота зуба
,
який забезпечує нормальну роботу
передачі. Із наведених співвідношень
випливає, що висота зуба
![]() .
.
Для діаметрів кіл вершин і западин одержимо такі формули:
![]() ,
(3.10)
,
(3.10)
![]() .
(3.11)
.
(3.11)
У наведених формулах нижні знаки відносяться до колеса з внутрішніми зуб’ями.
В
практиці іноді використовують зубчасті
колеса із вкороченою висотою зуба. У
таких колесах
![]() і
і
![]() .
.
В залежності від числа зуб’їв Z діаметр основного кола db може бути більшим або меншим за діаметром кола западин df. При рівності цих діаметрів на основі формул (3.13) і (3.19) одержуємо
![]() ,
,
звідки Z=41,7.
Якщо Z > 41, то db < df і весь профіль зуба нормального колеса окреслюється евольвентою.
Якщо Z > 41, то db < df і тільки частина профілю зуба між колом вершин і основним колом окреслюється евольвентою. Ділянка профілю між основним колом і колом западин виходить автоматично при нарізанні колеса і залежить від форми інструменту і способу нарізання. На рисунках профіль зуба на цій ділянці зображають прямою лінією, напрямленою по радіусу, і роблять закруглення (галтель) радіуса 0,38m, з’єднуючи профіль зуба з колом западин.
У колеса а внутрішніми зуб’ями мають місце аналогічні співвідношення. Але при внутрішніх зуб’ях весь профіль зуба має бути окресленим евольвентою. Цій умові задовольняють тільки колеса з числом зуб’їв Z > 33. Тому нормальне колесо з внутрішніми зуб'ями повинно мати не менше 34' зуб'їв.
