2.6. Визначення радіуса кривизни траєкторії

Кінематичний аналіз дозволяє визначити радіус кривизни траєкторії в будь-якій точці. Нехай деяка точка S при русі механізму описує траєкторію δδ ( рис.2.8,а). Даному положенню точки S, показаному на рис.2.8,а відповідає конкретний (відповідний) план механізму. Для цього положення механізму будуємо план швидкостей і план прискорень, визначиємо швидкість і прискорення точки S. На рис 2.8,б швидкість V_S зображена відрізком , відкладеним від полюса р, а прискорення відрізком , відкладеним від полюса p' (рис.2.8,в).

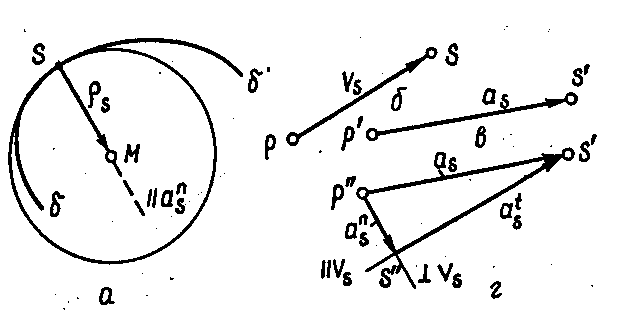
Рис.2.8. Визначення радіуса кривизни траєкторії: а - траєкторія б-б точки δ; б - швидкість точки S; в - прискорення точки S; г - нормальне і тангенціальне прискорення точки S

Розкладемо прискорення точки S на дві складові: нормальне і тангенціальне (рис.2.8,г). Тангенціальне прискорення напрямлене паралельно вектору ,а нормальне - перпендикулярно вектору . Відклавши від точки р'' вектор і розклавши його на дві складові за вказаними напрямками, одержимо величину і напрямок цих складових.

Нормальне прискорення зв’язане з радіусом кривизни і швидкість рівнянням

,

звідки .

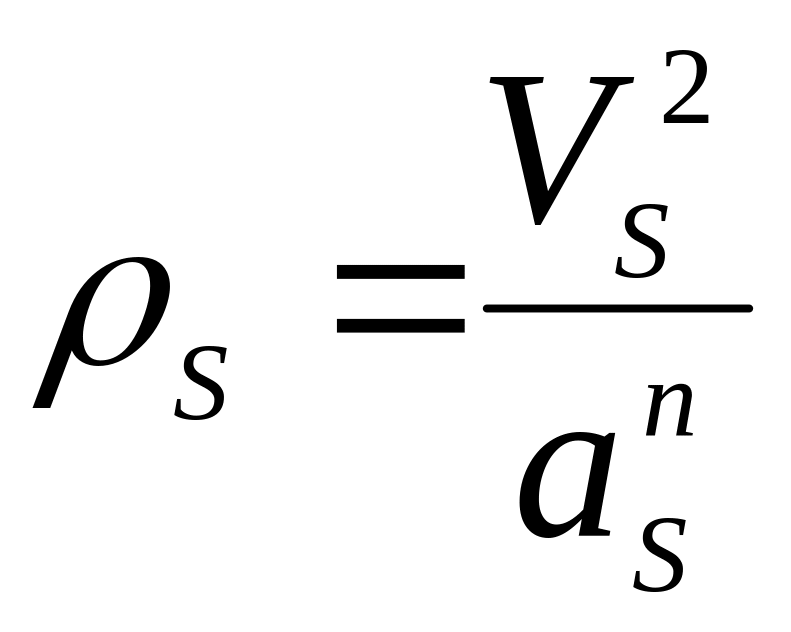Нормальне прискорення завжди напрямлене до центра кривизни траєкторії. Тому, провівши через точку S, лінію паралельно і відклавши від точки S величину радіуса кривизни ρ_S у напрямку нормального прискорення, одержимо положення центра кривизни M.

Опишемо навколо точки М коло радіуса ρ_S. Це коло називається кругом кривизни. Воно повинно збігатися із траєкторією δδ на деякій ділянці кривої.

2.7. Дослідження механізмів методом кінематичних діаграм

Кінематичними діаграмами називаються графіки зміни кінематичних параметрів переміщення, швидкості та прискорення будь-якої точки або ланки механізму залежно від часу або узагальненої координати.

Розглянемо побудову кінематичних діаграм , , для повзуна (точки В) кривошипно-повзунного механізму (див.рис.2.1).

Для побудови діаграми переміщень необхідно спочатку побудувати декілька планів механізму, наприклад 8, як це показано на рис.2.1. Переміщення S повзуна від його початкового (крайнього) положення (наприклад, від верхньої мертвої точки) будемо вимірювати відрізками , , , тощо. Отже, переміщення , тощо.

Побудуємо прямокутну систему координат (рис.2.9,а). Нa осі абсцис діаграми відкладемо відрізок , який зображає час одного оберту кривошипа (період) або кут повороту кривошипа Визначаємо масштабний коефіцієнт часу

, с/мм,

де n - частота обертання кривошипа, хв^-1.

Відрізок 0D ділимо на таку ж кількість рівних частин, на яку поділена траєкторія точки А кривошипа на рис.2.1. Точки 0,1,2, ... діаграми відповідають моментам часу, коли механізм займає відповідне положення. По осі ординат від точки 1,2,3, ... відкладаємо відповідні переміщення точки В у вигляді відрізків , , і т.д. при масштабному коефіцієнті . Якщо відрізки , на діаграмі будуть відповідно рівні відрізкам , … на планах механізму, то і масштабні коефіцієнти К_s i K_l будуть рівні (К_s = K_l). З'єднавши точки 0,1 ,2 , ... плавною кривою, одержимо діаграму переміщень повзуна (точки В) кривошипно-повзунного механізму.

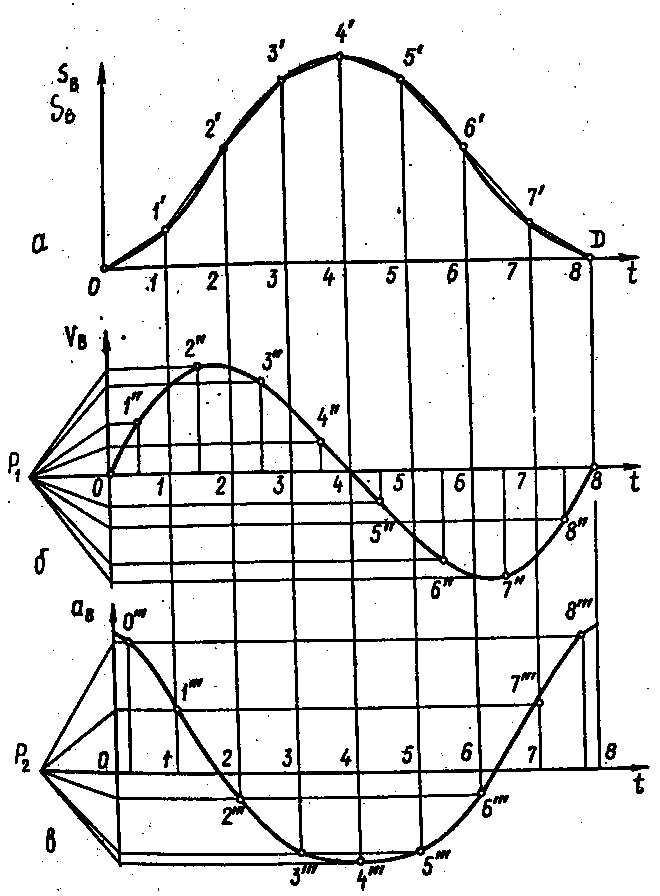
Рис.2.9. Побудова діаграми швидкостей і прискорень методами графічного диференціювання: а – діаграма переміщення точки В; б – діаграма швидкостей точки В; в – діаграма прискорення точки В

Для побудови діаграм і використовуюсь метод графічного диференціювання.

Під діаграмою будуємо нову прямокутну систему координат , вісь абсцис ділимо на відрізки так само, як і на діаграмі . На осі абсцис вліво від початку координат відкладаємо відрізок довільної довжини. Відстань називається полюсною відстанню.

Тoчки 0,1', 2', 3', ... діаграми з’єднуємо хордами 0 - 1', 1' - 2', 2' - 3' … .З точки p₁ діаграми проводимо промені паралельно цим хордам до перетину з віссю ординат. Від одержаних на осі ординат точок проводимо прямі паралельно осі абсцис до перетину з ординатами, які проведені через середини відповідних відрізків на осі абсцис. Одержуємо точки 1'', 2'', 3'' ... . З’єднавши точки 0, 1", 2", ... плавною кривою, одержуємо діаграму швидкостей (точки В).

Масштабний коефіцієнт осі ординат діаграми , визначаємо за формулою

.

Так само методом графічного диференціювання діаграми можна одержати діаграму прискорень повзуна (рис.2.9,в). Масштабний коефіцієнт діаграми визначається за формулою

.

Побудовані діаграми дозволить визначити швидкість і прискорення точки В в будь-якому положенні механізму.