3.14. Способы определения потерь напора при равномерном движении жидкости

Основной формулой при расчёте напорных трубопроводов явля­е­т­ся формула Дарси-Вейсбаха:

,

а при расчёте течений в открытых руслах – формула Шези:

.

Применение этих формул связано с определением коэффициен­тов  и С.

При ламинарном движении жидкости коэффициент  для труб определяется по формуле

. (3.43)

Впервые наиболее исчерпывающие данные о значении  были получены Никурадзе. Результаты показаны на рис. 3.19.

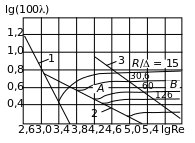
Рис. 3.19

В пределах прямой 1 коэффициент  зависит не от шерохо­ва­тости стенок трубы, а от числа Re (см. формулу 3.43). Прямая 2 представляет зависимость для гидравлических гладких труб, у которых шероховатость меньше толщины ламинарного при­стенного слоя.

Коэффициент  для гидравлических гладких труб определяется по формуле Блазиуса (прямая 2):

(3.44)

Между линиями 2 и линией 3 слева располагается зона А, в ко­то­рой  зависит как от числа Рейнольдса, так и от шероховатости по­верхности стенок труб.

Для определения  в этой области может применяться формула А. Д. Альтшуля:

, (3.45)

где kэ –

эквивалентная равномерно зернистая шероховатость, опре­де­ляемая опытным путем.

В области Б коэффициент  зависит только от шероховатости.

Для определения  в этой области рекомендуется формула Никурадзе

, (3.46)

где r –	радиус трубы;
 –	абсолютная шероховатость стенок трубы.

Сущеструют формулы Ф. А. Шевелёва, Н. З. Френкеля, Л. А. Тепакса, Б. Н. Шифринсона, Н. Ф. Фёдорова и других.

3.15. Местные гидравлические сопротивления

Местные сопротивления вызываются фасонными частями, ар­ма­турой и другими элементами трубопровода. При движении жид­кости на местных сопротивлениях изменяется величина и направ­ле­ние скорости.

Потери, связанные с преодолением местных сопротивлений, про­пор­циональны кинетической энергии потока:

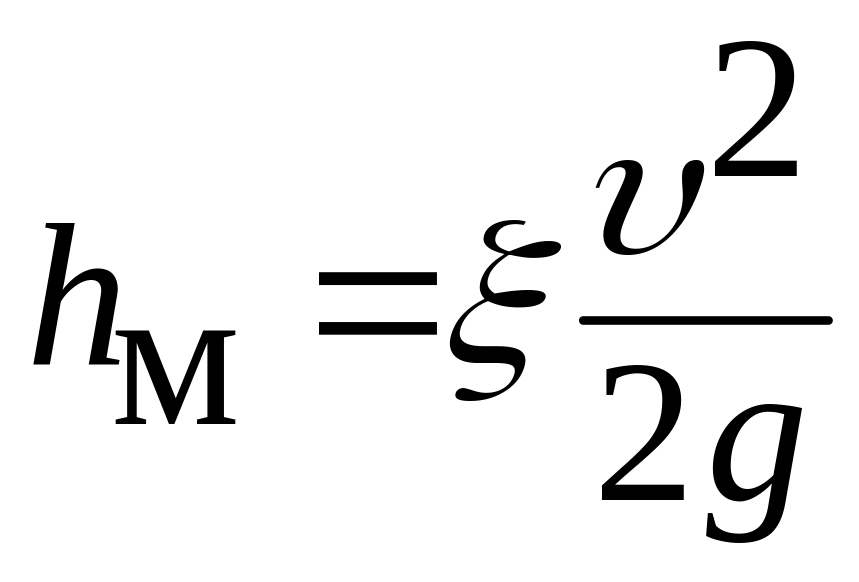, (3.47)

где м –

коэффициент местных сопротивлений зависит не только от вязкости и скорости движения основного потока, но главным образом от геометрической формы и размеров сопротивления.

При турбулентном режиме движения жидкости потери h_м зависят только от геометрических характеристик сопротивления.

Рассмотрим вопрос о потере напора при внезапном расширении трубопровода (рис. 3.20). Часть энергии в этом случае расходуется на сложное циркуляционное движение жидкости в кольцевом про­странстве между струёй и стенками трубы за сечением 1–1.

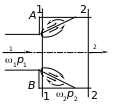
Рис. 3.20

Вследствие отрыва потока и связанного с ним вихреобразования на участке трубы между сечениями 1–1 и 2–2 наблюдаются зна­чи­тельные потери напора.

Учитывая, что давление на торцевой стенке АВ практически равно давлению на выходе из узкой части трубы р₁, найдём вели­чи­ну потерь по уравнению Бернулли:

(3.48)

Из теоремы импульсов для сечений 1–1 и 2–2 можно записать:

. (3.49)

Пренебрегая силами трения на участке 1–2 и учитывая, что , после деления на обеих частей уравнения (3.49) получим:

или

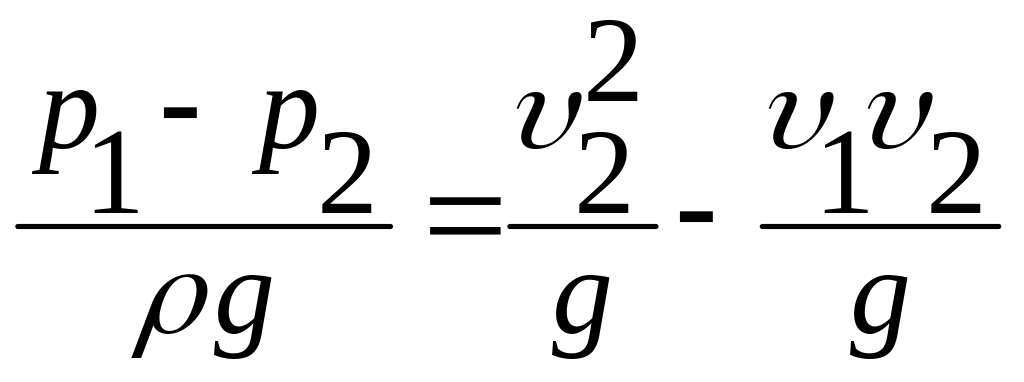. (3.50)

Подставляя выражение (3.50) в уравнение (3.48), найдём:

или

. (3.51)

То есть, потери напора при внезапном расширении равны ско­рост­ному напору от потерянной скорости. Выражение (3.51) назы­вается теоремой, или формулой Борда.

Формулу (3.51) можно привести к виду:

.

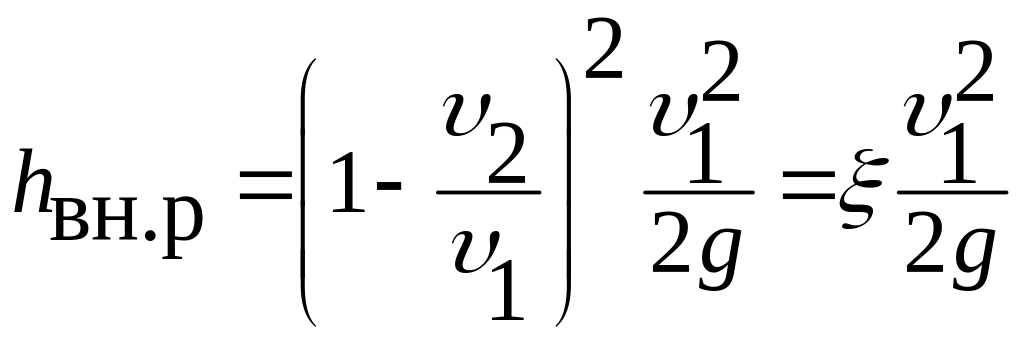С учётом того, что ₁₁ = ₂₂ и 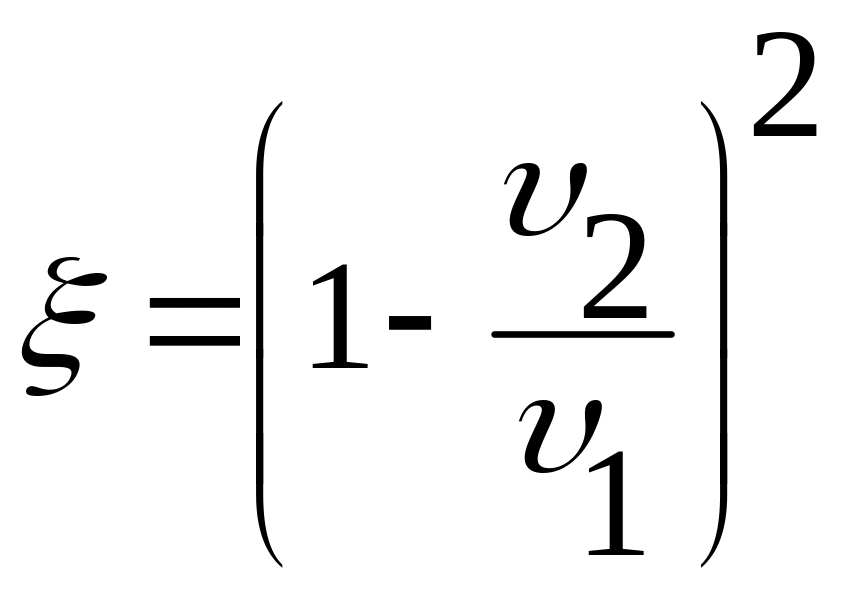, получим:

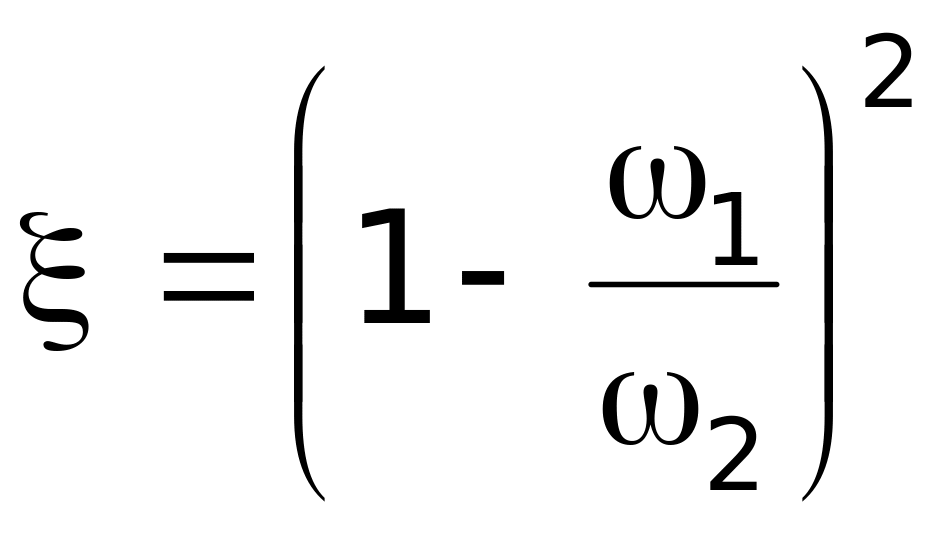– относится к скорости ₁;

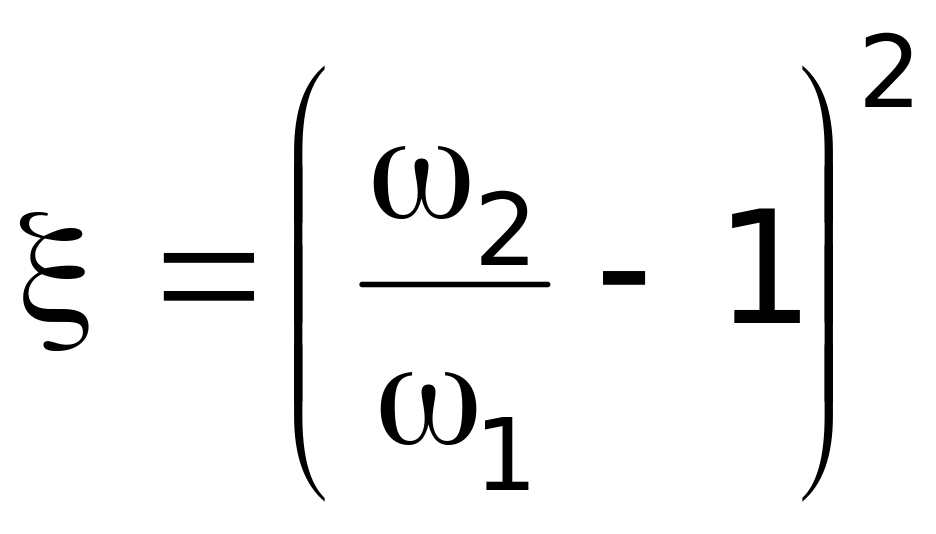– относится к скорости ₂.

Суммарные потери напора в трубопроводе постоянного диаметра

.
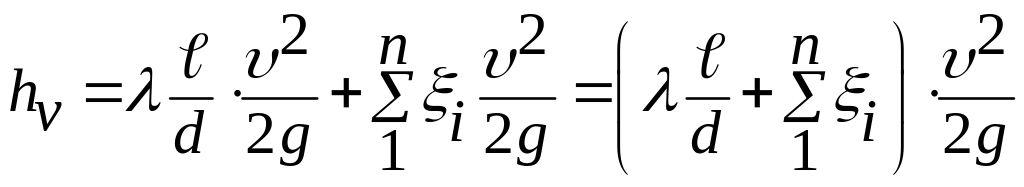