Задания для самостоятельной работы
ЗАДАНИЕ 1. Составить программы для решения следующих задач:
Варианты задания 1.
Даны два момента времени в часах, минутах и секундах (h1, m1, s1) и (h2, m2, s2). Определить, какое время раньше, первое или второе.
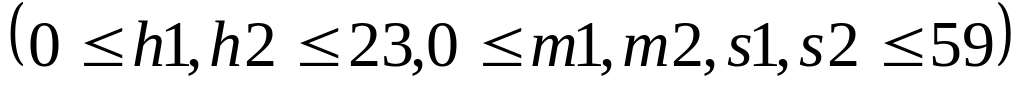
Заданы две даты (d1, m1, y1) и (d2, m2, y2). Определить, какая дата позднее.
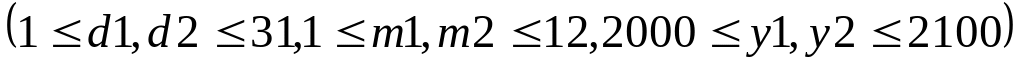
Даны длины сторон треугольника. Определить вид треугольника: “равносторонний”, “равнобедренный”, “разносторонний”. Для двух последних случаев предусмотреть случай “прямоугольный”.
Задано время в часах, минутах и секундах (h1, m1, s1). Определить время (h2, m2, s2), на одну секунду больше заданного.
Задана дата (d1, m1, y1) и (d2, m2, y2). Определить, какая дата позднее.
Даны длины сторон параллелограмма и одна из его диагоналей. Определить вид параллелограмма: ”ромб”, “прямоугольник”, “квадрат”, “параллелограмм”.
Даны длины двух сторон треугольника и угол (в градусах) между этими сторонами. Определить вид треугольника: “равносторонний”, “равнобедренный”, “разносторонний”. Для двух последних случаев предусмотреть случай “прямоугольный”.
Определить, какие корни в квадратном уравнении
:
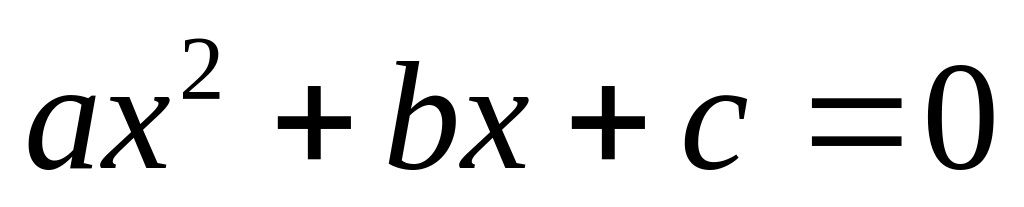действительных корней нет, корни
кратные, корни различные. В случае
наличия действительных корней, вывести
их значения.Даны три различных числа a, b, c. Переопределить значения переменных так, чтобы: a < b < c.
Даны два угла (в градусах) треугольника. Определить вид треугольника: “равносторонний”, “равнобедренный”, “разносторонний”. Для двух последних случаев предусмотреть случай “прямоугольный”.
Дано натуральное число N (N<100). Определить, верно ли, что
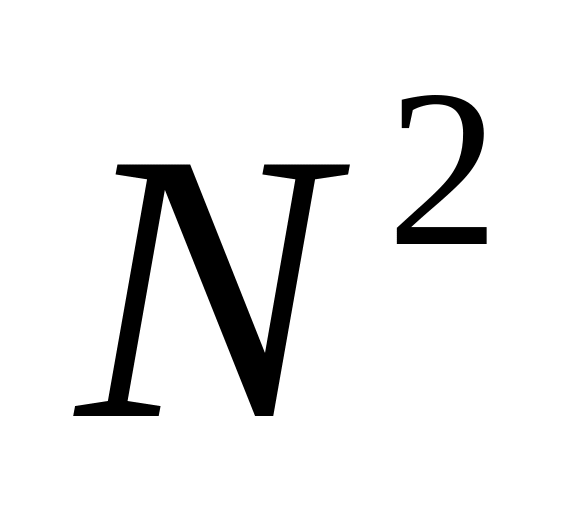равно
кубу суммы цифр числа N .Дано натуральное число N (N<10000). Определить, является ли это число перевертышем с учетом четырех цифр. Например, такими числами являются 2222, 1661, 0440.
Дано натуральное число N (N<10000). Определить, верно ли, что это число содержит ровно три одинаковые цифры, как, например, числа 2220, 6676, 0006.
Дано натуральное число N (N<10000). Определить, верно ли, что все четыре цифры числа различны, как, например, у чисел 1234, 0541.
Даны целые m, n (
),
указывающие момент времени: “m часов,
n минут”. Определить наименьшее время
(число полных минут), которое должно
пройти до того момента, когда часовая
и минутная стрелки на циферблате
совпадут.
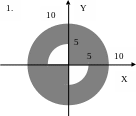
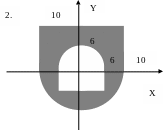
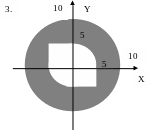
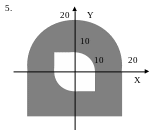
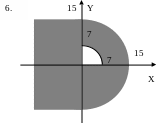
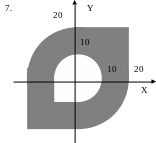
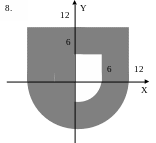
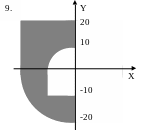
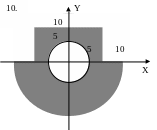
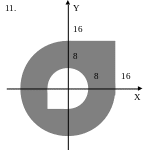
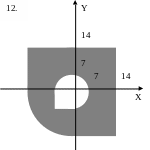
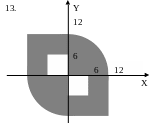
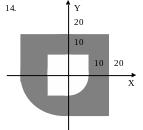
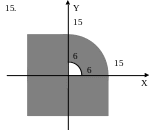
ЗАДАНИЕ 2. Составить программы для определения кратчайшего расстояния от заданной точки с координатами (X, Y) до границы фигуры, если:
точка находится вне фигуры (Для точки, находящейся внутри фигуры, выдать соответствующее сообщение.);
точка находится внутри фигуры (Для точки, находящейся вне фигуры, выдать соответствующее сообщение.).
Варианты задания 2.
