10. Модуль graph

Модуль GRAPH представляет собой библиотеку типов, констант, процедур и функций для работы в графических режимах. Модуль находится в файле GRAPH.TPU.

В графическом режиме экран представляет собой матрицу точек (пикселей). Любое изображение является совокупностью точек. Количество точек (разрешающая способность экрана) зависит от типа адаптера и режима его работы. Графический адаптер это специальная микросхема в компьютере, позволяющая управлять выводом на монитор графической информации. Для взаимодействия программы с адаптером необходим соответствующий графическому адаптеру драйвер – файл с расширением .BGI.

Процедуры и функции модуля graph

1. InitGraph (Var D, M: Integer; Path:String); - инициализация графического режима. Параметры: D – код драйвера; M – код режима работы; Path – путь к драйверу. Параметры D и M должны быть описаны в программе как переменные целого типа. Задать их можно в режиме автоопределения: если присвоить D значение константы Detect до использования процедуры, то задание драйвера и режима его работы произойдет автоматически, при этом выбирается режим с максимальным разрешением 640 x 480 пикселей и 16-цветовой палитрой. Параметр Path задается как строковая константа или переменная (в режиме автоопределения необходимо указать путь к файлу EGAVGA.BGI).

2. CloseGraph; - закрытие графического режима.

3. MoveTo (X, Y: Integer); - перемещение текущего указателя в точку с координатами (X, Y).

4. PutPixel (X, Y: Integer; C: Word); - установка пикселя (X, Y) цветом С.

5. Line (X1, Y1, X2, Y2: Integer); - построение отрезка между точками (X1, Y1) и (X2, Y2).

6. LineTo (X, Y: Integer); - построение отрезка от точки текущего указателя до точки с координатами (X, Y).

7. LineRel (dX, dY: Integer); - построение отрезка от точки текущего указателя до точки с координатами (X+dX, Y+dY), где (X, Y) – координаты точки текущего указателя..

8. Rectangle (X1, Y1, X2, Y2: Integer); - построение контура прямоугольника, где (X1, Y1) – координаты левой верхней точки прямоугольника, (X2, Y2) – правой нижней точки.

9. Bar (X1, Y1, X2, Y2: Integer); - построение закрашенного прямоугольника.

10. Circle (X, Y: Integer; R: Word); - построение окружности, где (X, Y) – координаты центра, R – радиус.

11. Ellipse (X, Y: Integer; NU, KU: Word; XR, YR: Word); - построение эллипса или дуги эллипса, где (X, Y) – координаты центра, NU, KU – величины углов в градусах, отсчитываемые против часовой стрелки от горизонтальной оси, проходящей через центр, до начальной и до конечной точек дуги эллипса соответственно, XR, YR – горизонтальная и вертикальная полуоси эллипса.

12. FillEllipse (X, Y: Integer; XR, YR: Word); - построение закрашенного эллипса.

13. Arc (X, Y: Integer; NU, KU, R: Word); - построение окружности или дуги окружности.

14. SetColor (C: Word); -установка текущего цвета, которым будут изображаться контуры фигур и тексты.

15. SetBkColor (C: Word); - установка цвета фона.

16. SetFillStyle (P, C: Word); - установка текущего орнамента P и текущего цвета заполнения фигур C.

17. FloodFill (X, Y: Integer; B: Word); - закрашивание области, ограниченной непрерывной линией. Здесь (X, Y) – координаты любой точки внутри области, B – цвет линии (контура), до которой производится закрашивание.

18. SetLineStyle (S, P, T:Word); - установка текущих параметров линии, где S -стиль, P - шаблон, T – толщина.

19. SetTextStyle (F, D, S: Word); - установка текущих параметров шрифта: F - тип, D - направление выдачи текста, S - размер символов.

20. OutTextXY (X, Y: Integer; S: String); - вывод строки символов S, начиная с точки с координатами (X,Y).

21. OutText (S: String); - вывод строки символов S, начиная с точки текущего указателя.

22. ClearDevice; - очистка графического экрана.

23. SetViewPort (X1, Y1, X2, Y2: Integer; F: Boolean); - установка графического окна. Здесь F – ограничитель: если F=True, то все построения проводятся только в пределах окна.

24. ClearViewPort; - очистка окна.

25. GetMaxX: Integer; - определение максимального значения координаты Х.

26. GetMaxY: Integer; - определение максимального значения координаты Y.

Пример 18. Построить график функции .

Program Example_18;

Uses Graph;

Const mas=30; {масштаб - количество пикселей в единичном отрезке}

Var gd, gm, c, mx, my, mx2, my2: Integer; x, y: Real; s: String;

Begin

gd:= Detect;

InitGraph(gd, gm, 'c:\lang\tp7\bgi'); {инициализация графического режима}

mx:=GetMaxX; my:=GetMaxY; {определение максимальных значений координат}

mx2:=mx div 2; my2:=my div 2; {определение вспомогательных переменных}

Line(0, my2, mx, my2); {ось X проходит по середине экрана}

MoveTo(mx2-10, 10); LineRel(10, -10); LineRel(10, 10); {стрелка направления оси X}

SetTextStyle(0, 0, 1);

For c:=-10 to 10 do {цикл для разметки оси X на интервале [-10, 10]}

If c<>0 Then

Begin

Line(mx2+c*mas, my2-5, mx2+c*mas, my2+5);

Str(c, s); OutTextXY(mx2+c*mas, my2+6, s)

End;

Line(mx2, 0, mx2, my); {ось Y проходит по середине экрана}

MoveTo(mx-10, my2-10); LineRel(10, 10); LineRel(-10, 10);{стрелка на оси Y}

For c:=-7 to 7 do {цикл для разметки оси Y на интервале [-7, 7]}

If c<>0 Then

Begin

Line(mx2-5, my2+c*mas, mx2+5, my2+c*mas);

Str(c, s); OutTextXY(mx2+6, my2-c*mas, s)

End;

x:=-5; y:=0.5*x*x-5;

MoveTo(round(mx2+x*mas), round(my2-y*mas)); {установка нач. точки графика}

While x<=5 do {цикл для построения графика в виде ломаной на интервале [-5,5]}

Begin

x:=x+0.1; y:=0.5*x*x-5;

LineTo(round(mx2+x*mas), round(my2-y*mas))

End;

{обозначение осей, начала координат и графика функции}

SetTextStyle(0, 0, 2);

OutTextXY(mx2+10, 10, 'X'); OutTextXY(mx -20, my2+20, 'Y');

OutTextXY(mx2+10, my2+10, '0'); OutTextXY(mx-160, 100, 'y=0,5x-5');

SetTextStyle(0, 0, 1); OutTextXY(mx-65, 95, '2');

Readln; {задержка содержимого экрана}

CloseGraph {закрытие графического режима}

End.

Пример 19. Построить заданное изображение, применив какой-нибудь способ раскраски, и размножить его на экране (получить не менее трех изображений).

Пояснение к программе. Центры окружностей (x,y) одинакового радиуса r расположены на одной дуге окружности с центром, совпадающим с центром самой маленькой окружности (x0,y0), через определенные углы u.

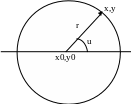
Используя полярную систему координат, рассчитаем координаты центров окружностей: x= x0+ r*cos(u); y= y0- r*sin(u) (знак ‘-’ используется из-за направления Y сверху вниз).

Program Example_19;

Uses Graph;

Var gd, gm: Integer;

{***процедура построения одного изображения***}

Procedure Izo(x0, y0: Integer); {x0, y0 - координаты центра маленькой окружности}

Var k, r, rc, x, y, x0, y0, i, j: Integer; u: Real;

Begin

k:=1; {количество окружностей на дуге одного радиуса}

rc:=5; {радиус окружностей, располагающихся на одной дуге}

r:=0; {радиус дуги}

For i:=1 to 4 do {цикл по количеству дуг, включая дугу для маленькой окружности}

Begin

u:=0;

For j:=1 to k do {цикл по количеству окружностей на одной дуге}

Begin

{рассчитываем полярные координаты центра окружности}

x:=round(x0+r*cos(u)); y:=round(y0-r*sin(u));

SetColor(k); Circle(x, y, rc); {строим окружность цветом k}

SetFillStyle(1, k); FloodFill(x, y, k); {закрашиваем ее тем же цветом}

If k<>1 Then u:=u+Pi/(k-1) {увеличиваем угол для центра след. окружности}

End;

k:=k+2; rc:=rc+5; r:=r+5+2*rc {изменяем все параметры для следующей дуги}

End;

End; {конец описания процедуры}

Begin {начало программы}

gd:=Detect;

InitGraph(gd, gm, 'c:\lang\tp7\bgi');

{три раза обращаемся к процедуре – получаем три изображения на экране}

Izo(160, 185); Izo(480, 185); Izo(320, 385);

Readln;

CloseGraph

End.