Алгоритм 8 Расчет коэффициента ранговой корреляции Спирмена rs

1. Определить, какие два признака или две иерархии признаков будут участвовать в сопоставлении как переменные А и В.

2. Проранжировать значения переменной А, начисляя ранг 1 наименьшему значению. Занести ранги в первый столбец таблицы.

3. Проранжировать значения переменной В. Занести ранги во второй столбец таблицы.

4.Подсчитать разности d между рангами А и В по каждой строке таблицы и занести в третий столбец таблицы.

5. Возвести каждую разность в квадрат (d²). Эти значения занести в четвертый столбец таблицы.

6.Подсчитать сумму квадратов ∑d².

7. При наличии одинаковых рангов рассчитать поправки:

Та=∑(а³ - а)/12; Тb=∑(b³ - b)/12, где а - объем каждой группы одинаковых рангов в ранговом ряду А; b - объем каждой группы одинаковых рангов в ранговом ряду В.

8.Рассчитатъ коэффициент ранговой корреляции по формуле:

а) при отсутствии одинаковых рангов

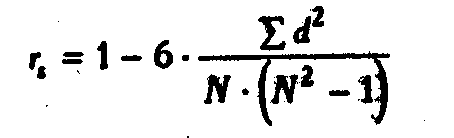
б) при наличии одинаковых рангов

где ∑d². - сумма квадратов разностей между рангами; Та и Тb - поправки на одинаковые ранги; N - количество испытуемых или признаков, участвовавших в ранжировании.

9. Определить по Табл. ХVII Приложения 2 критические значения rs для данного N. Если rs превышает критическое значение или, по крайней мере, равен ему, корреляция достоверно отличается от 0.

Алгоритм 9 Расчет коэффициента корреляции Пирсона rxy

1. Определить, какие два признака будут участвовать в сопоставлении, как переменные х и у.

2. Подсчитать общую сумму для каждой переменной отдельно (∑х и ∑у).

3. Найти среднее арифметическое значение для х и у.

Мх=∑х/N Му=∑у/N

4. Найти величины отклонений каждого из первичных результатов от Мх и Му и заносим в 4, 5 столбец таблицы: xi=Мх-х; yi=Му-у.

5. Возвести каждое отклонение xi, yi в квадрат: xi², yi². Заносим результата в 6, 7 столбец таблицы.

6. Найти значения среднего квадратичного отклонения для каждой переменной по формулам: σх= 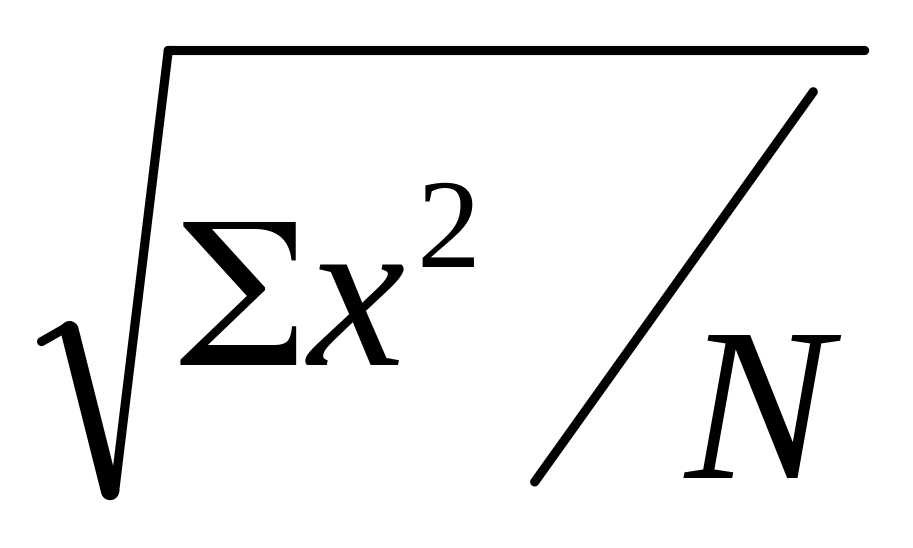; σу=

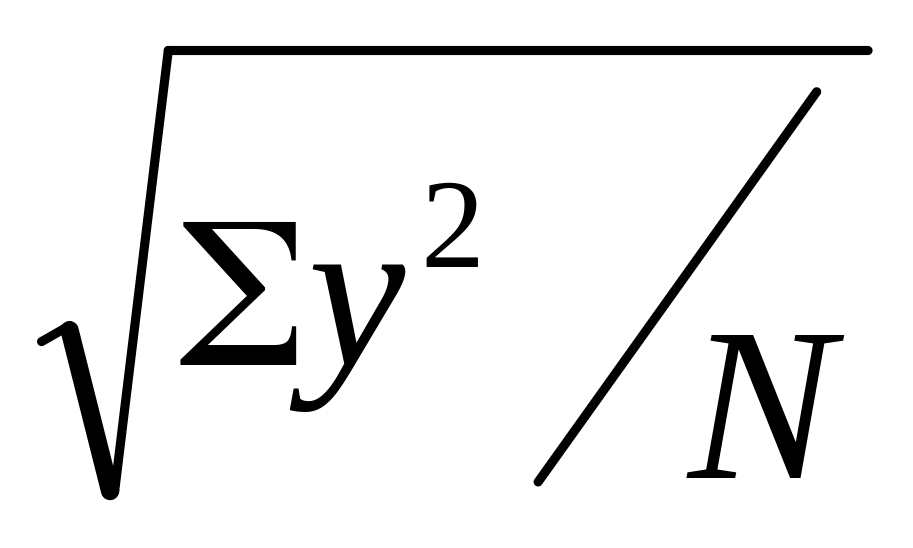
7. Определить произведения для каждой пары отклонений xi, yi. Значения занести в 8 столбец таблицы.

8. Рассчитать коэффициент корреляции по формуле:

rху= ∑(хi ∙ уi) / (N∙ σх∙ σу); где хi – отклонение величины Х от средне арифметической Мх;

уi - отклонение величины Y от средне арифметической Му; N – объем выборки сравниваемых пар первичных результатов; σх – среднеквадратичное отклонение для первичных результатов Х; σу - среднеквадратичное отклонение для первичных результатов Y.

9. Определить по таблице XVI критических значений rху для данного N. Если rху превышает критические значения или равен ему, корреляция достоверно отличается от нуля.

Приложение 2

Таблицы критических значений

Таблица I

Критические значения критерия Q Розенбаума для уровней статистической значимости

p≤0,05 и p≤0,01

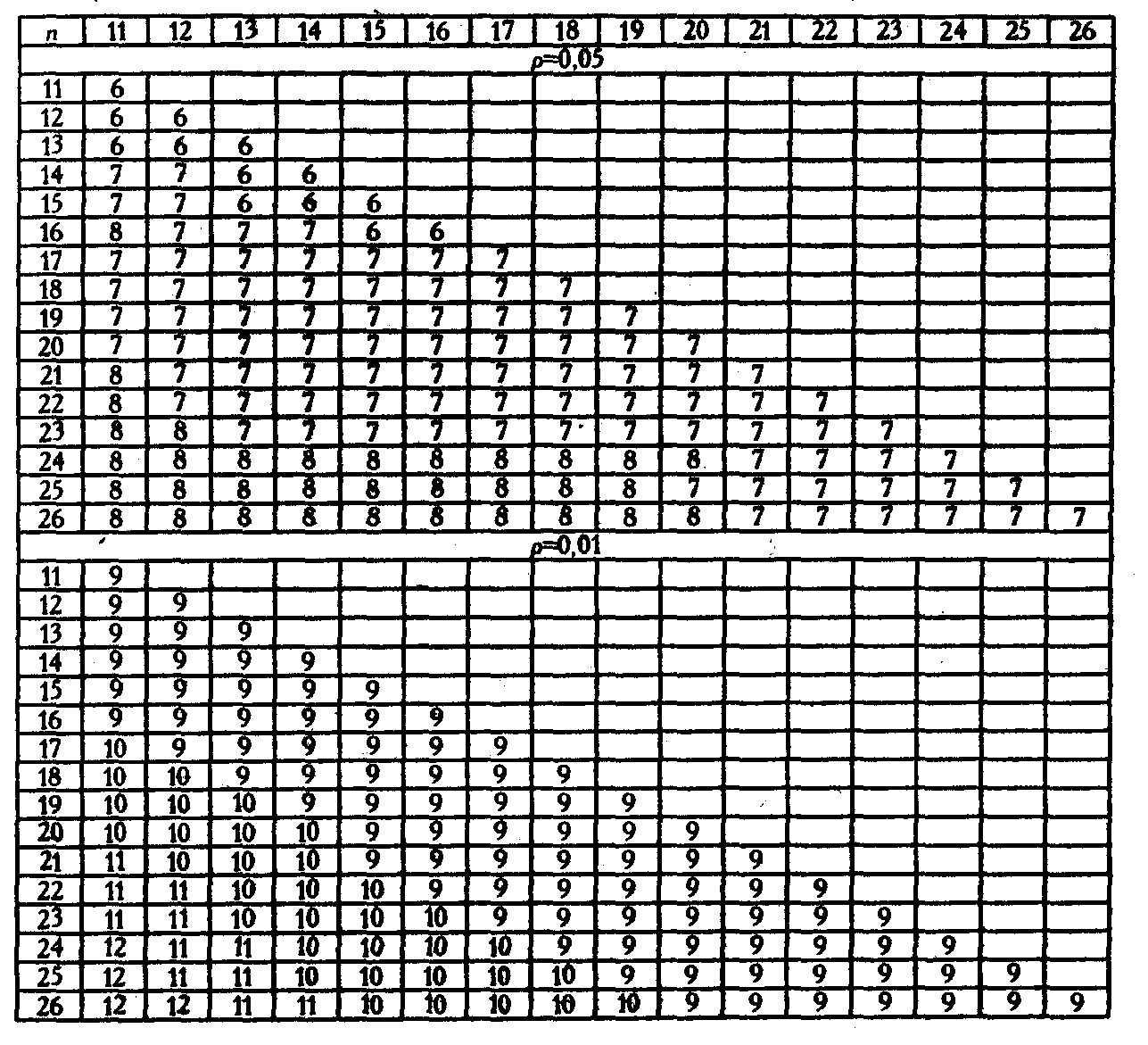
Таблица II

Критические значения критерия U Манна-Уитни для уровней статистической значимости p≤0,05 и p≤0,01

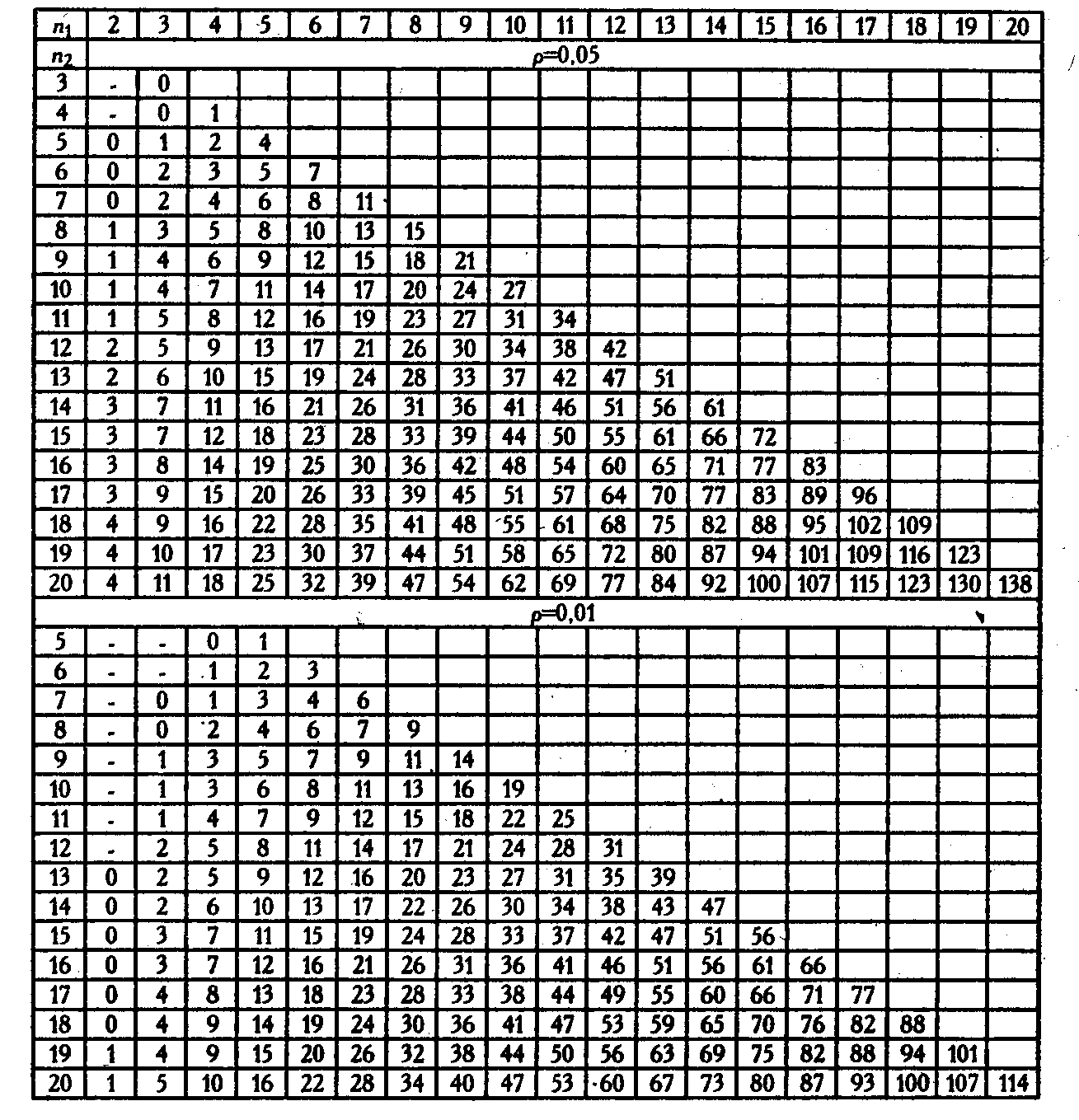
Таблица II. Продолжение

Таблица II. Продолжение

Таблица II. Продолжение

Таблица II. Продолжение

Таблица II. Окончание

Таблица III

Критические значения критерия H Крускала-Уоллиса

для разных сочетаний n1, n2 и n3

Таблица V

Критические значения критерия G для уровней

статистической значимости p≤0,05 и p≤0,01

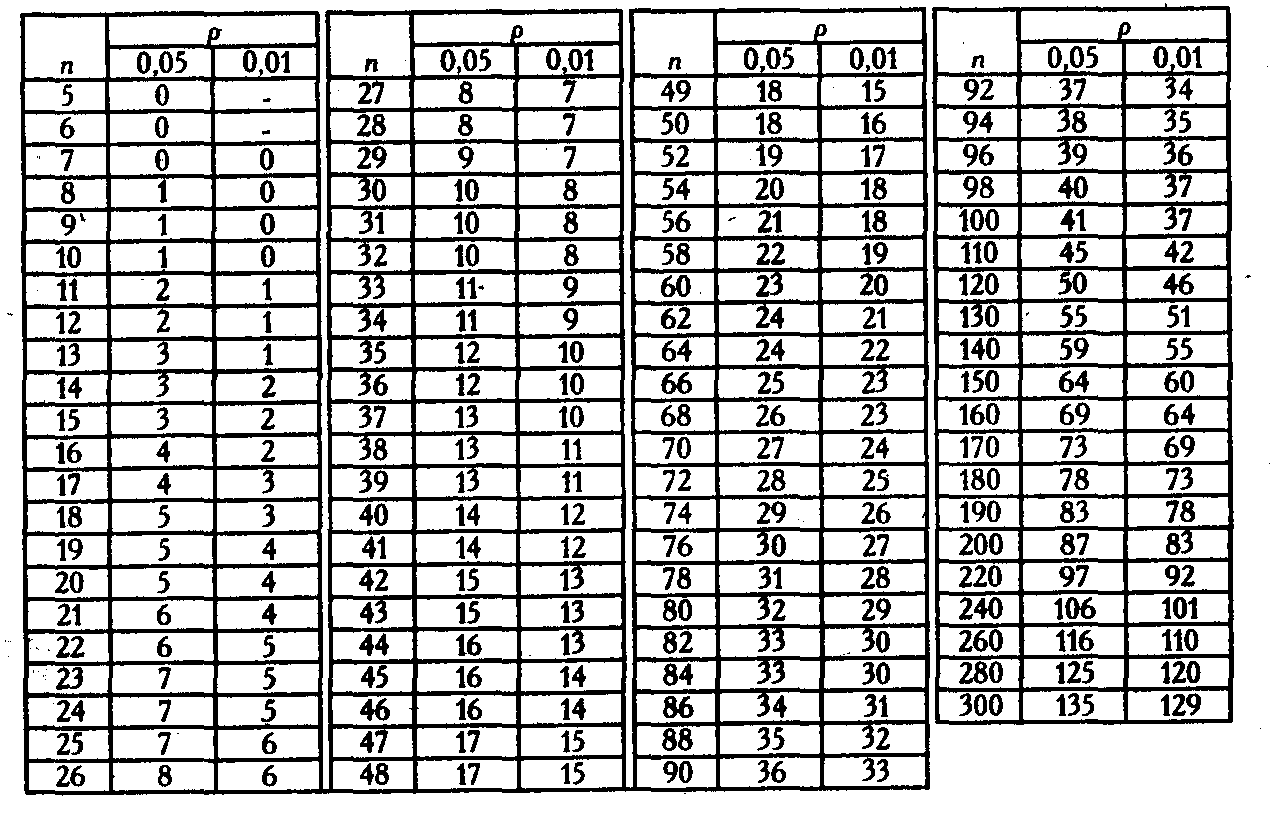
Таблица VII-А

Критические значения критерия Фридмана для количества условий c=3 и количества испытуемых от двух до девяти (2≤n≤9)

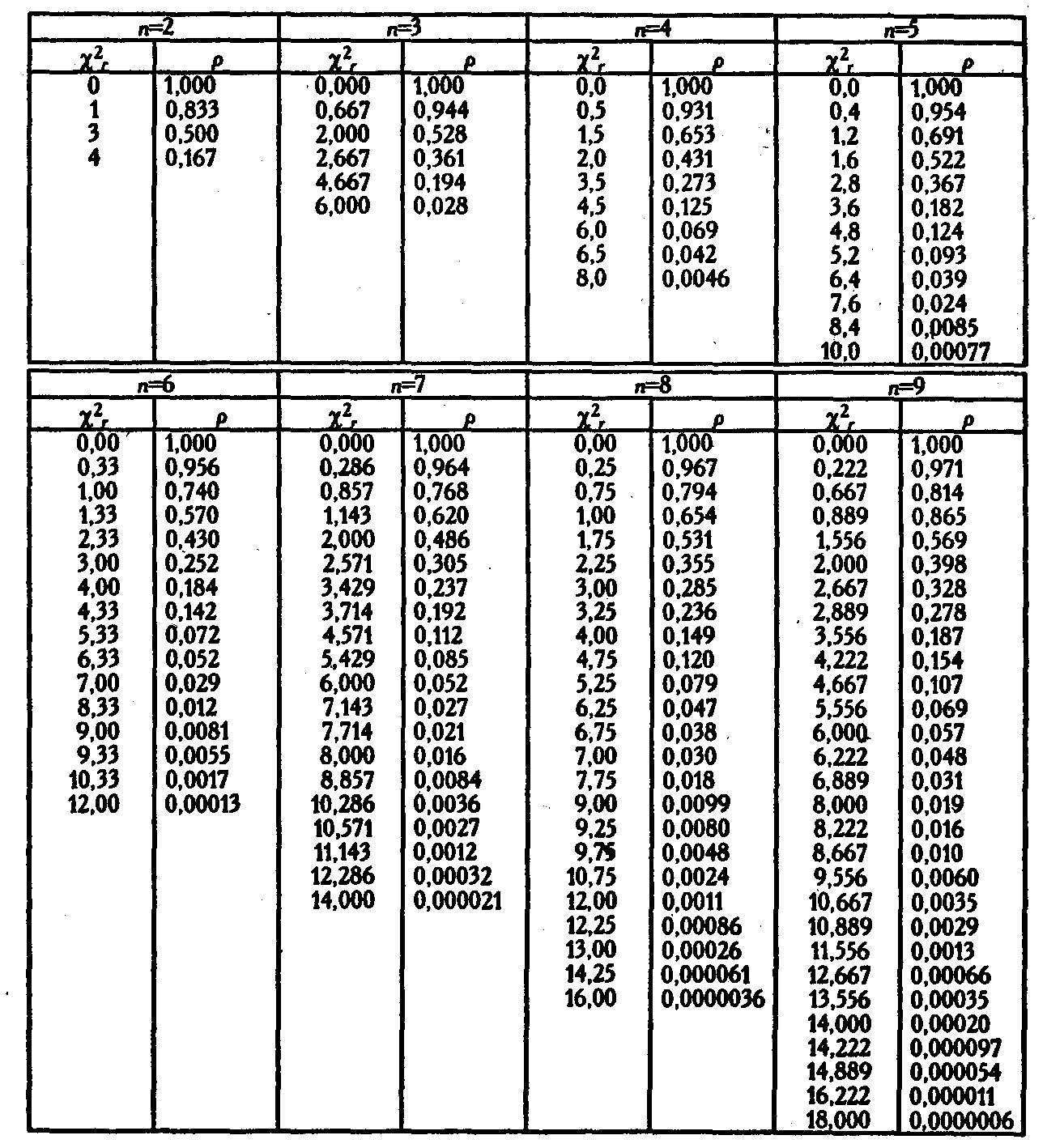
Таблица VII-Б

Критические значения критерия Фридмана для количества условий c=4

и количества испытуемых от двух до четырех (2≤n≤4)

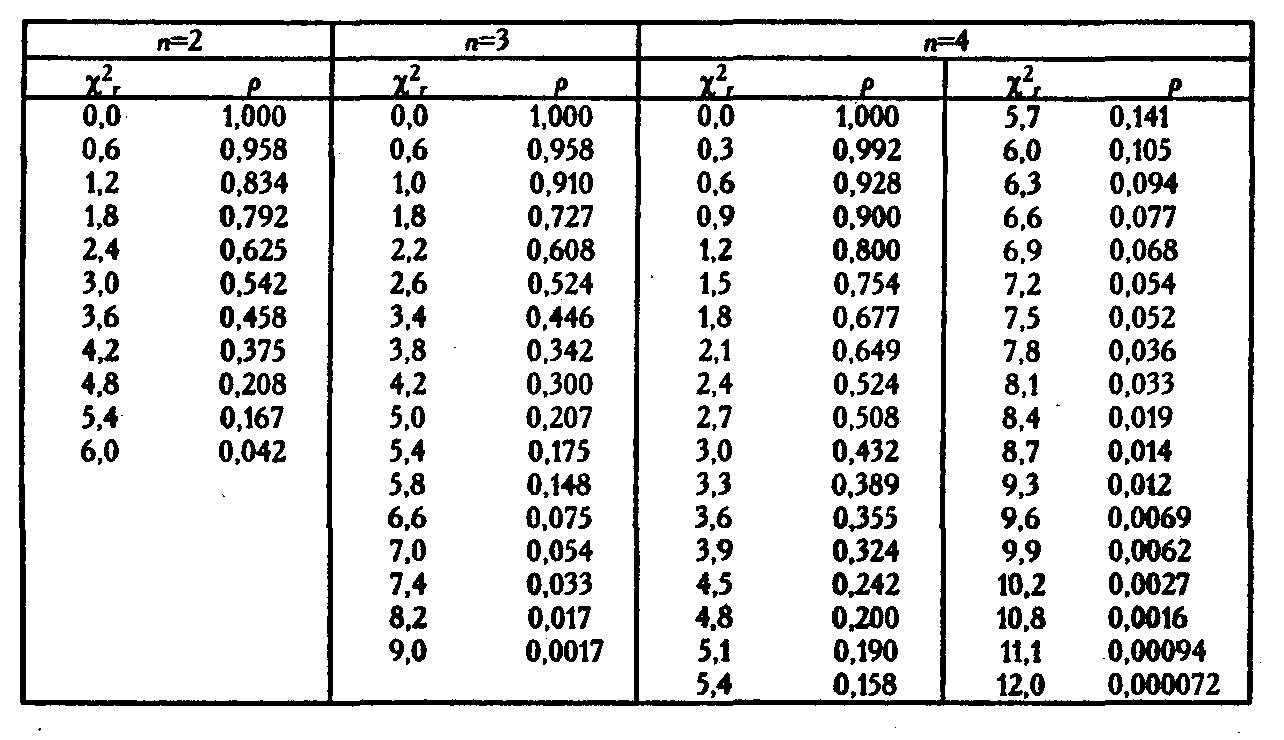
Таблица IX

Критические значения критерия χ² для уровней статистической значимости p≤0,05 и p≤0,01 при разном числе степеней свободы ν

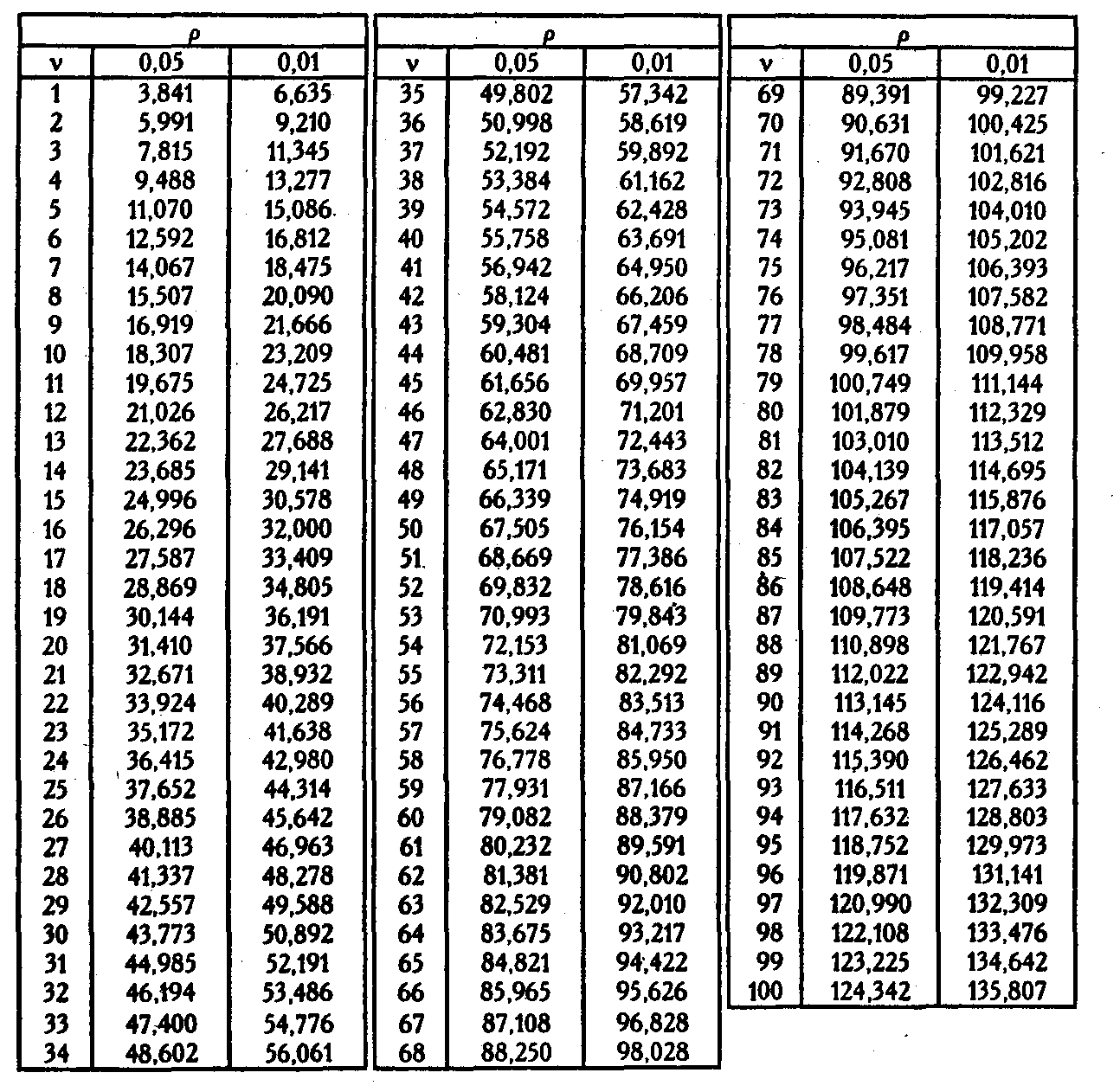
Источник: Сидоренко Е.В. Методы математической обработки в психологии. – СПб.: ООО «Речь», 2004.

Таблица XII

Величины угла φ (в радианах) для разных процентных долей: φ=2∙arcsin√P

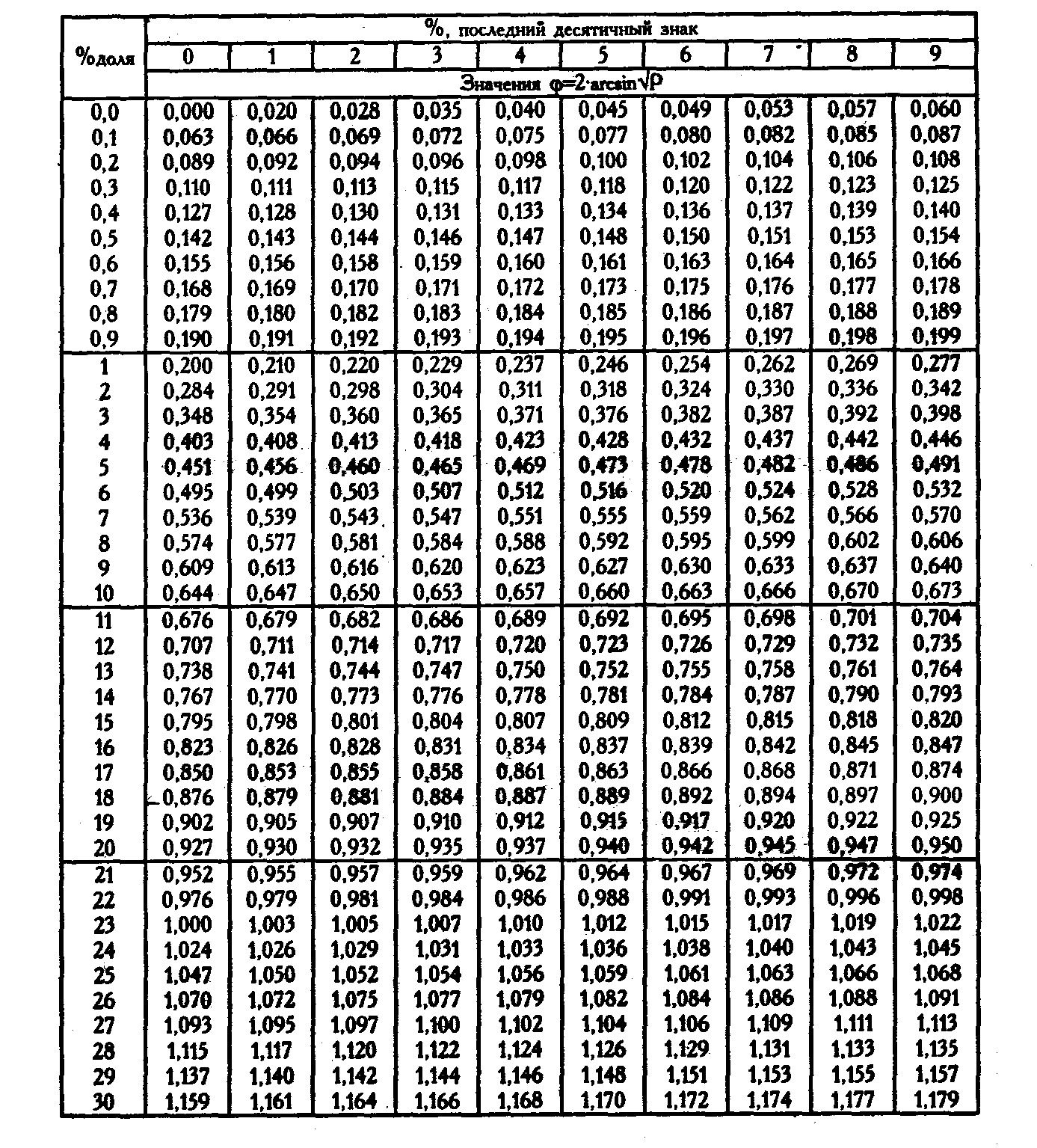
Таблица XII. Продолжение

Таблица XII. Окончание

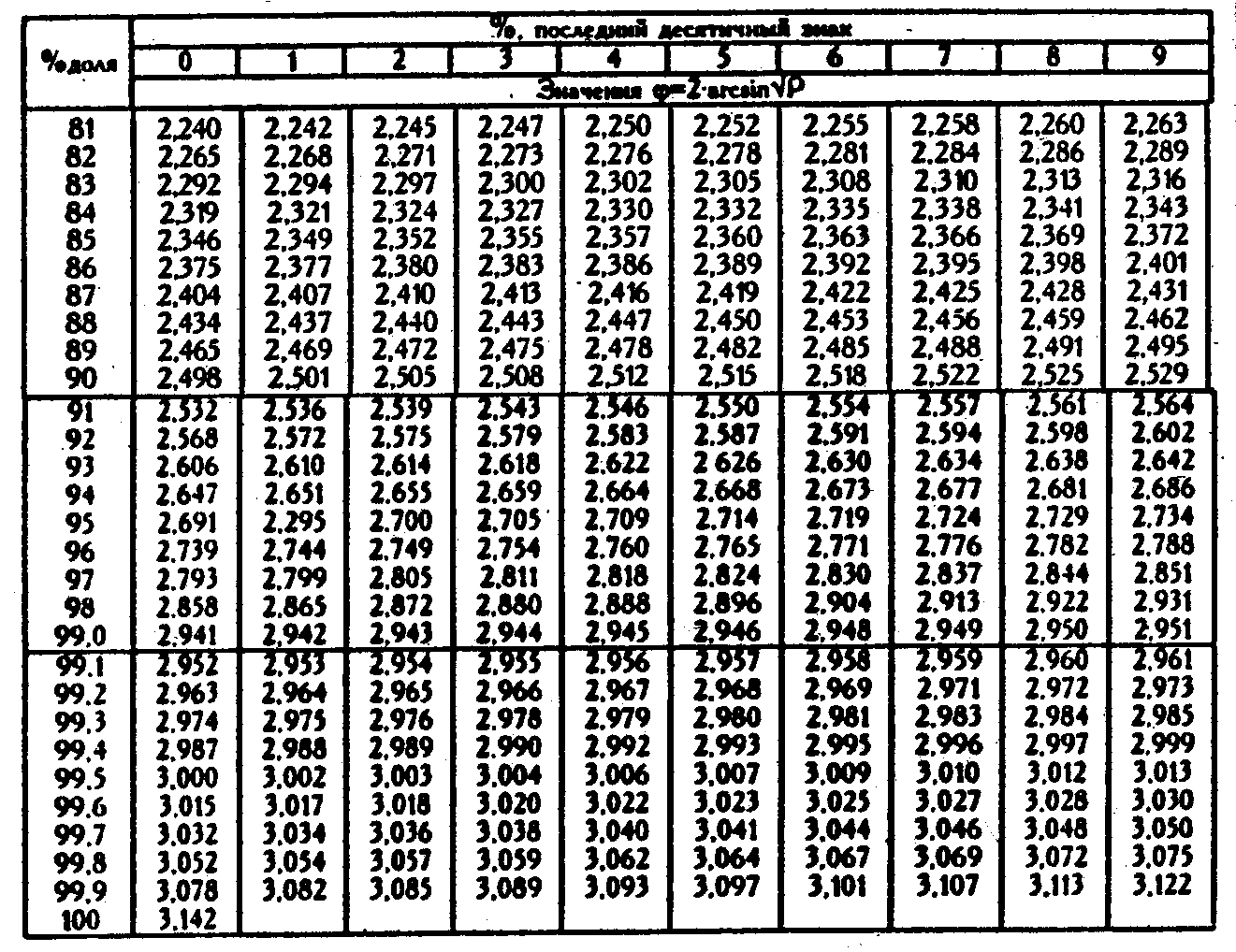
Таблица XVI

Критические значения коэффициента корреляции rxy Пирсона

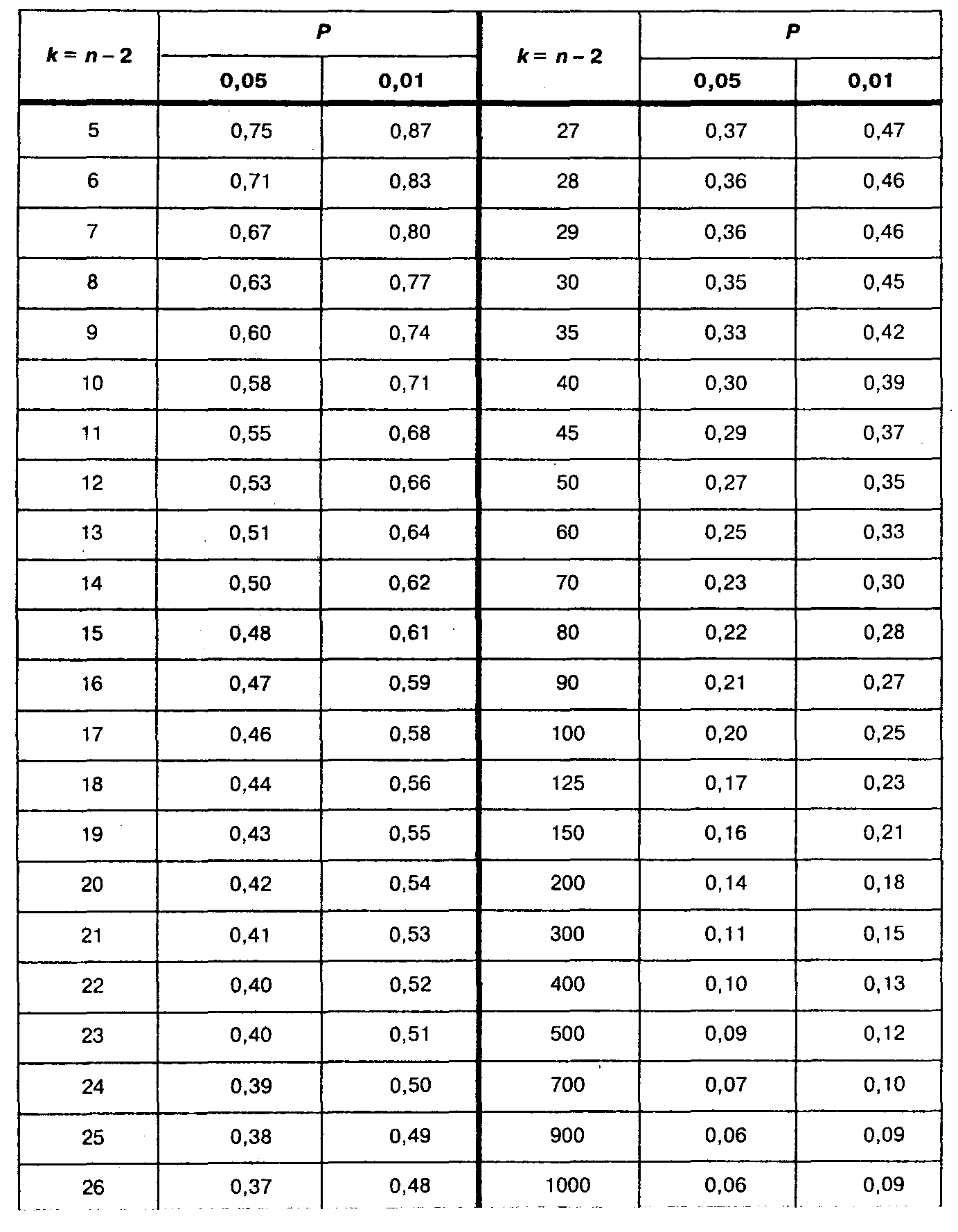
Таблица XVII

Критические значения коэффициента корреляции рангов Спирмена

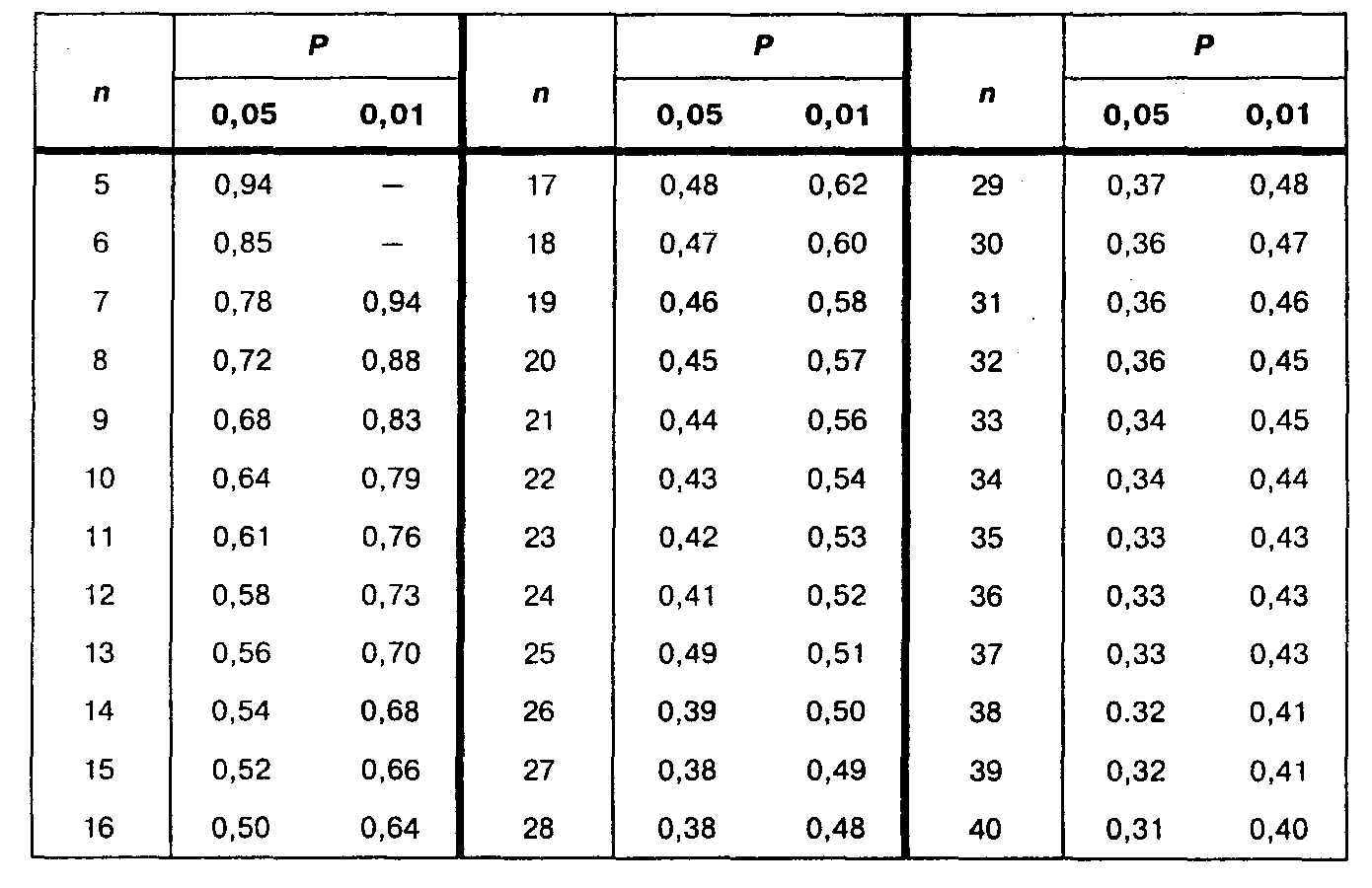
Приложение 3