1.6. Зубчатые колеса,

изготовляемые со смещением исходного контура.

В станочном зацеплении рейки и изготовляемого зубчатого колеса делительная прямая рейки может касаться и не касаться делительной окружности колеса. В первом случае колесо называется изготовленным без смещения исходного контура, а во втором – со смещением. Величина смещения исходного контура определяется произведением модуля m на коэффициент смещения Х. Если рейка смещается от центра заготовки, то принимается Х>0 и колесо называется положительным, если к центру – то Х<0 и колесо называется отрицательным. При Х=0 зубчатое колесо называется нулевым.

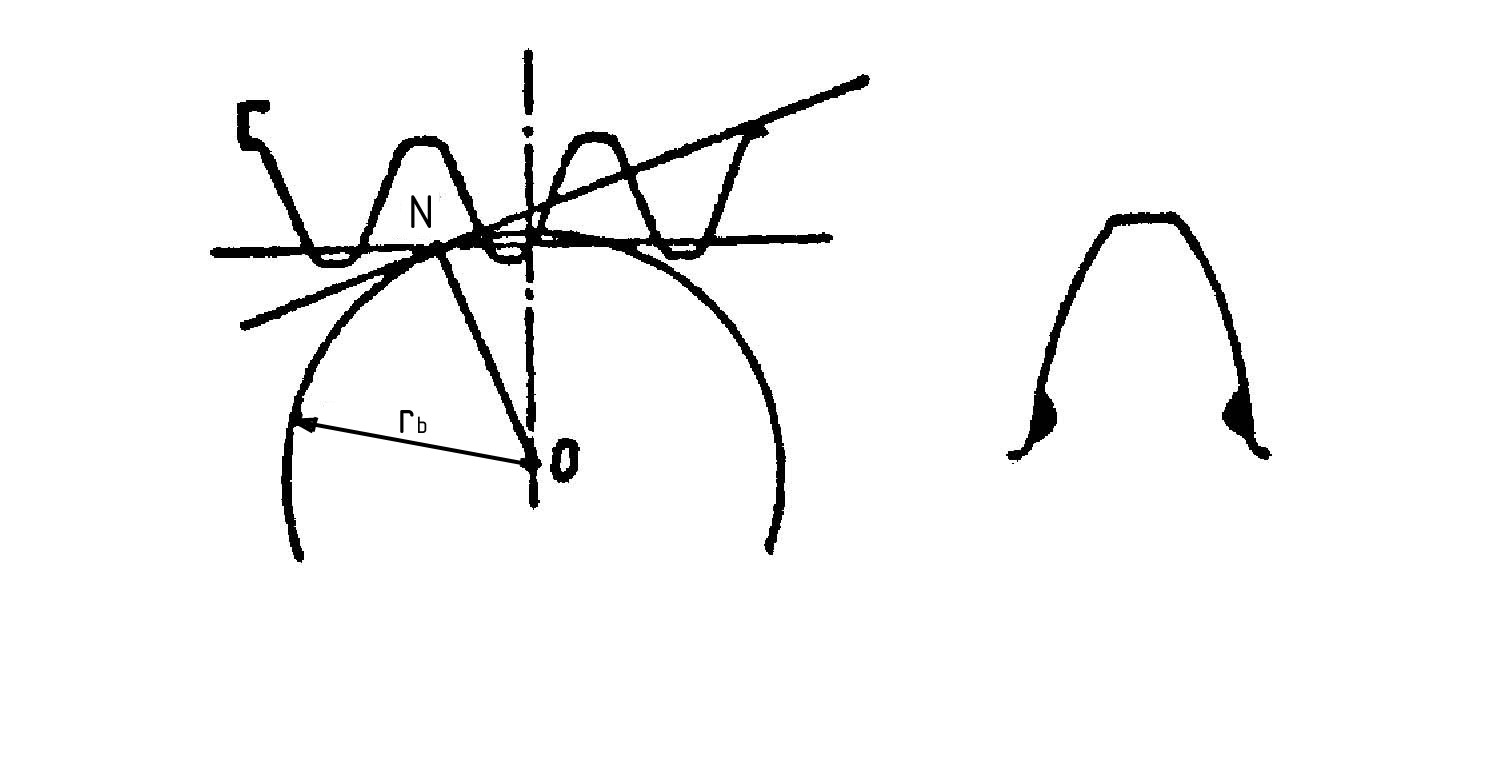
а) б)

Рис.10. Подрезание зубьев.

Если при нарезании зубьев колеса прямая головок пересекает линию зацепления ниже точки N (рис.10 а)), то возникает явление подреза (рис.10 б)), при котором часть металла ножки зуба удаляется режущим инструментом, что ослабляет зуб в опасном (на изгиб) сечении.

Чтобы исключить подрез, рейку смещают от центра заготовки на столько, чтобы прямая головок проходила через или выше точки N (рис.10 а)). Из этого условия находится минимальное число зубьев, которое можно нарезать без подреза ножки, т.е.

и при стандартном исходном контуре равно 17.

При изготовлении зубчатых колес минимальный коэффициент смещения, обеспечивающий отсутствие явления подреза, определяется из выражения

или для стандартного исходного контура

(4)

Из (4) следует, что при Z >17 подрез ножки зуба будет отсутствовать даже при отрицательном смещении инструмента.

При положительном смещении исходного контура толщина зуба по делительной окружности увеличивается, а по окружности вершин уменьшается. Поэтому максимальный коэффициент смещения ограничивается условием заострения зубьев и определяется из выражения

где - угол профиля зуба по окружности головок зубьев.

Можно заметить, что наряду с явлением подреза при изготовлении колес по методу обката могут наблюдаться и другие искажения эвольвентного профиля, например, интерференция /1/.

1.7. Коэффициент перекрытия.

Для непрерывной передачи движения от одного колеса к другому необходимо, чтобы следующая пара зубьев вступала в зацепление не позже, чем предыдущая пара выйдет из зацепления. Это условие выполняется при , где и -дуги зацепления (рис.6), а - шаг по начальной окружности.

Дугой зацепления называют дугу по начальной окружности, которую описывает соответствующая точка зуба, находящегося в зацеплении с зубом парного колеса.

Численно условие непрерывности зацепления оценивают коэффициентом перекрытия

где - угол перекрытия (центральный угол дуги зацепления),

- угловой шаг зубьев.

Коэффициент перекрытия показывает среднее число пар зубьев, находящихся одновременно в зацеплении, и характеризует плавность передачи. В строительном машиностроении рекомендуется .

1.8. Коэффициент удельного скольжения.

При относительном движении зацепляющихся зубьев происходит качение и скольжение одной эвольвентной поверхности по другой. Скольжение зубцов увеличивает потери на трение в передаче и приводит к износу рабочих поверхностей зубьев. Для оценки скольжения зубьев используют коэффициент удельного скольжения или просто удельное скольжение , под которым понимают отношение скорости скольжения контактной точки к скорости общей точки по поверхности зуба данного зубчатого колеса в направлении скольжения.

Удельное скольжение зубца первого колеса по зубцу второго и второго по первому равно:

;

;

где - радиусы кривизны профилей зубцов в точке контакта (соответственно N₁K и N₂K по рис.4),

- передаточное отношение,

- скорость скольжения.

В полюсе зацепления скорость скольжения и удельное скольжение равны нулю. Наибольшее удельное скольжение возникает в нижних точках активных профилей зубьев.