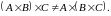Національний технічний університет України
«Київський політехнічний інститут»
Методичні вказівки
до типової розрахункової роботи
з математичного аналізу
Вступ до математичного аналізу.
Диференціальне та інтегральне числення
функцій однієї змінної.
Київ - 2013
Множини та дії над ними Основні поняття
Поняття множини є одним з найбільш важливих первісних, не означуваних понять математики. Для раціонального аналізу навколишнього світу його уявляють складеним із окремих «об’єктів». Виділення цих об’єктів та зібрань є природнім способом організації математичного мислення.
Під
множиною
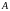 ми розуміємо довільне зібрання визначених
же різних об’єктів, що розглядаються
як єдине ціле. Об’єкти, з яких складається
множина, називаються її елементами.
Поняття елемента теж є первісним.
ми розуміємо довільне зібрання визначених
же різних об’єктів, що розглядаються
як єдине ціле. Об’єкти, з яких складається
множина, називаються її елементами.
Поняття елемента теж є первісним.
Той
факт, що об’єкт
 є елементом множини
,
позначається символом
є елементом множини
,
позначається символом
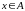 (читається «
належить
»).
Якщо
не є елементом
,
це позначається
(читається «
належить
»).
Якщо
не є елементом
,
це позначається
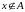 (читається «
не належить
»).
Множина, що не має елементів, називається
порожньою і позначається символом
(читається «
не належить
»).
Множина, що не має елементів, називається
порожньою і позначається символом
 .
.
Таким чином, множина вважається заданою, якщо про кожний «об’єкт», що розглядається, можна сказати, що він або належить множині , або ні.
Отже, кожна множина характеризується певною ознакою, згідно якої довільний елемент належить чи не належить даній множині.
Приклади множин:
Множина
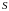 всіх символів цієї сторінки.
всіх символів цієї сторінки.Множина
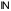 натуральних чисел (позначається
натуральних чисел (позначається
 ).
).Множина
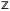 цілих чисел (позначається
цілих чисел (позначається
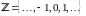 ).
).Множина
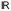 дійсних чисел.
дійсних чисел.
Звичайно
в конкретних міркуваннях елементи всіх
множин, що розглядаються в даній
математичній теорії, вибирають із деякої
широкої множини
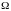 (своєї для кожного випадку), яка називається
універсальною множиною, або універсумом.
(своєї для кожного випадку), яка називається
універсальною множиною, або універсумом.
Щоб задати множину, потрібно вказати, які елементи їй належать. Це можна зробити двома способами:
Прямим перечисленням елементів множини.
Якщо
множина
складається з елементів
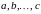 ,
це позначається як
,
це позначається як
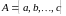 .
.
Характеристичною властивістю (ознакою) елементів множини.
Якщо
А — множина всіх елементів
універсуму, що мають дану властивість
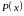 ,
це позначається:
,
це позначається:
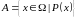 ,
або
,
або
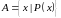 ,
чи
,
чи
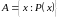 .
.
Приклади множин:
Множина
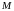 парних цілих чисел запишеться как
парних цілих чисел запишеться как
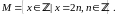
Множина
 раціональних чисел:
раціональних чисел:
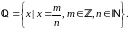
Дві
множини
і
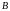 називаються рівними, якщо кожний елемент
множини
є елементом множини
і навпаки. Рівність множин
і
позначається як
називаються рівними, якщо кожний елемент
множини
є елементом множини
і навпаки. Рівність множин
і
позначається як
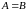 .
.
З
означення рівності випливає, що рівні
множини складаються з одних і тих же
елементів, причому порядок розміщення
елементів множин неістотний, наприклад,
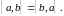
Дії над множинами
Включення.
Множина називається підмножиною множини , якщо кожний елемент множини є елементом множини . Символічно:
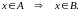
Це
позначають як
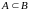 або
або
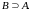 Порожня множина
вважається підмножиною будь-якої
множини:
Порожня множина
вважається підмножиною будь-якої
множини:
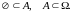
Зауважимо,
що множини рівні тоді і тільки тоді,
коли
і
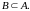
Операції над множинами можна символічно задати геометричними фігурами на площині.
Зображення включення .
Об’єднання.
Об’єднанням
множин
і
називається множина, що складається з
тих елементів, які належать принаймні
одній із множин
або
(позначають
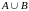 ),
тобто
),
тобто
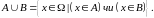
Зображення об’єднання .
Властивості операції об’єднання:
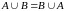 (комутативність),
(комутативність),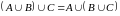 (асоціативність),
(асоціативність),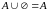 ,
,
де
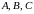 — довільні множини з універсуму
.
— довільні множини з універсуму
.
Перетин.
Перетином
множин
і
називається множина, що складається із
спільніх елементів множин
і
(позначають
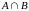 ),
тобто
),
тобто
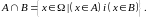
Зображення перетину .
Властивості операції перетину:
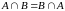 (комутативність),
(комутативність),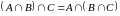 (асоціативність),
(асоціативність), ,
,
де — довільні множини з універсуму .
Операції об’єднання та перетину пов’язані між собою двома дистрибутивними законами:
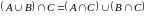 ,
,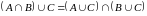 ,
,
де — довільні множини з універсуму .
Різниця.
Різницею
множин
і
називається множина, що складається з
усіх тих елементів множини
,
що не належать множині
(позначають
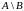 ),
тобто
),
тобто
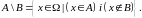
Зображення різниці .
Доповнення.
Доповненням
до множини
називається множина
 (позначають
(позначають
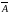 ),
тобто
),
тобто
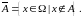
Зображення доповнення .
Властивості операції доповнення:
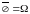 ,
,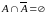 ,
,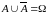 ,
,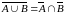 (перший
закон двоїстості),
(перший
закон двоїстості),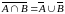 (другий
закон двоїстості).
(другий
закон двоїстості).
Симетрична різниця.
Симетричною різницею множин і називається множина
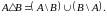
Зображення
симетричної різниці
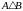 .
.
Властивості симетричної різниці:
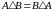 (комутативність),
(комутативність),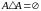 ,
,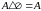 .
.
Прямий добуток.
Впорядкованою
парою елементів
 і
і
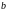 називається множина
називається множина
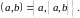
Елемент
називається першим елементом пари, а
елемент
— другим. Спорядковані пари
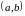 і
і
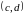 рівні тоді і тільки тоді, коли рівні їх
відповідні елементи
рівні тоді і тільки тоді, коли рівні їх
відповідні елементи
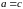 і
і
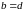 :
:
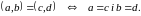
Зауважимо,
що при
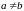 маємо, що
маємо, що
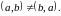
Прямим
добутком множин
і
називається множина відповідних пар,
в яких перший елемент належить множині
,
а другий — множині
(позначають
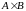 ),
тобто
),
тобто
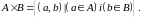
Приклади прямого добутку:
Нехай
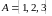 ,
,
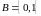 .
.
Тоді
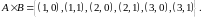
Нехай
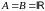 .
Тоді прямий добуток
.
Тоді прямий добуток
 є множиною всіх впорядкованих пар
дійсних чисел і позначається
є множиною всіх впорядкованих пар
дійсних чисел і позначається
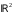 .
Отже
.
Отже
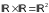 .
Відомо, що вибравши систему координат
на площині, можна кожну точку площини
задати впорядкованою парою чисел. Метод
координат застосував у XVII
ст. французький математик і філософ
Рене Декарт, тому прямий добуток іноді
називають декартовим.
.
Відомо, що вибравши систему координат
на площині, можна кожну точку площини
задати впорядкованою парою чисел. Метод
координат застосував у XVII
ст. французький математик і філософ
Рене Декарт, тому прямий добуток іноді
називають декартовим.
Зауважимо, що для прямого добутку, взагалі кажучи,
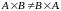
За
аналогією з впорядкованою парою можна
ввести поняття впорядкованої трійки
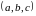 елементів множин
елементів множин
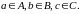
За означенням впорядкована трійка
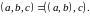
Дві
впорядковані трійки
і
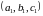 рівні тоді і тільки тоді, коли
рівні тоді і тільки тоді, коли
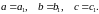
Множина
всіх впорядкованих трійок елементів
множин
називається прямим (декартовим) добутком
цих множин і позначається
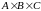 .
Тобто
.
Тобто
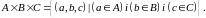
Зауважимо, що взагалі кажучи,