Неопределённость вида
Пример 10. Найти а)
,
б)
Решение.
Ответ: а) 0, б)
Неопределённость вида
Для раскрытия данной неопределённости
необходимо сначала привести её к виду
или
,
что можно сделать, убрав один из множителей
в знаменатель как обратную величину,
т.е.
.
Раскрытие получающихся неопределённостей
рассмотрено ранее.
Пример 11. Найти а)
,
б)
Решение.
а)
б)
Ответ: а) 1, б) 3
Непрерывность функции
Пример 12.
Решение. В точке
функция
не является непрерывной. Существуют
и конечный предел
,
но
.
Следовательно, точка
является точкой устранимого разрыва .
График функции имеет следующий вид:
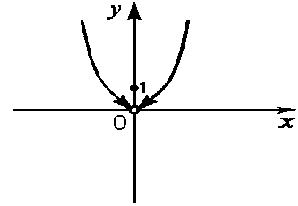
Пример 13. Функция задана различными аналитическими выражениями для различных областей изменения аргумента х:
Найти односторонние пределы и скачок функции в точках разрыва и построить график.
Решение. Данная функция определена
и непрерывна в интервалах
.
При
меняется аналитическое выражение
функции и только в этой единственной
точке функция может иметь разрыв.
Определим односторонние пределы функции в этой точке:
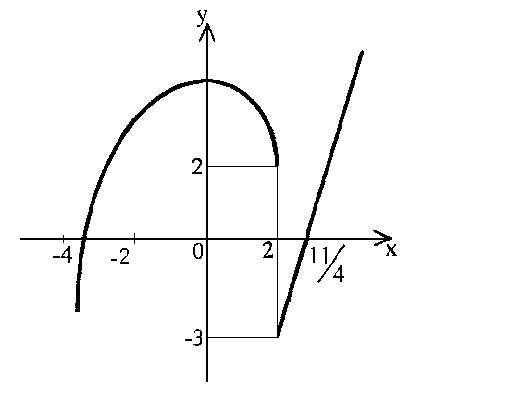
Так как односторонние пределы функции
в точке
не равны между собой, то в этой точке
функция имеет разрыв I
рода. Скачок функции равен:
График функции имеет следующий вид:
Пример 14. Дана функция
.
Исследовать ее на непрерывность.
Решение. Областью определения данной
функции является интервал
,
т.к.
,
т.е. в точке
будет разрыв. Определим, какого же рода
он будет. Для этого рассмотрим односторонние
пределы функции в точке
:
(т.к.
,
то
,
значит
,
а
при
Следовательно,
)
(т.к.
,
то
,
значит
,
а
при
Следовательно,
)
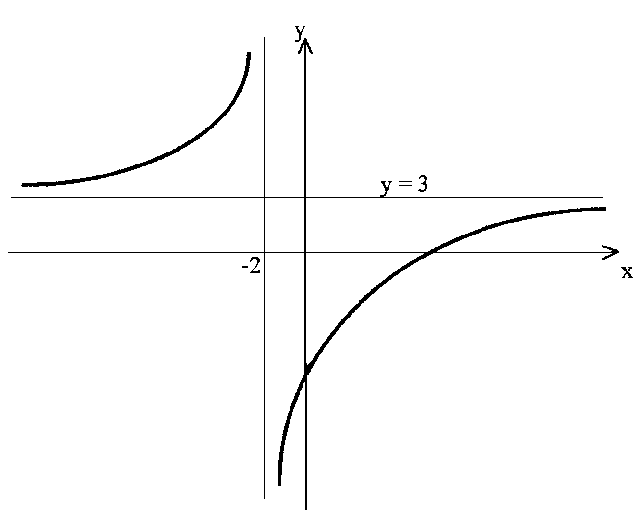
Таким образом, в точке данная функция имеет разрыв II рода.
Данная функция является дробно-линейной. Графиком дробно-линейной функции служит равносторонняя гипербола, асимптоты которой параллельны осям координат.
Дифференциальное исчисление Вычисление производных от элементарных функций
Теорема:
Если функции
и
заданы в окрестности точки
,
а в самой точке имеются конечные
производные, то функции
где
и
- постоянные,
а в случае
и
также имеют в точке
конечные производные. При этом имеют
место формулы:
(1)
(2)
(3)
- где значения всех
функций взяты при
.
Таблица производных простейших элементарных функций:
Рассмотрим примеры вычисления производных.
Пример 1:
Найти
и
,
если
Решение:
По правилу дифференцирования частного
(3) находим общее выражение для производной
(полагаем
Подставляя в
значения
и
,
находим частные значения производной:
Ответ:
Пример 2:
Найти
Решение:
Сначала получим правило дифференцирования
произведения
воспользовавшись (2).
Имеем
Применим
его для вычисления
Тогда
Ответ:
Пример 3: Продифференцировать функции:
а)
б)
в)
Решение:
а) 
Правила дифференцирования можно применять в “уме”, не делая столь подробных записей.
б) 
так как
.
в)
Ответ:
а)
;
б)
;
в)
