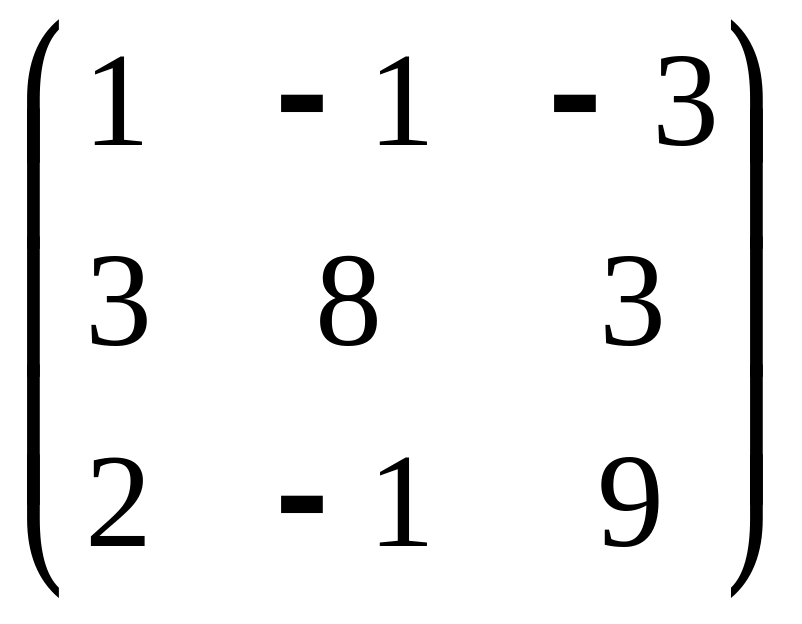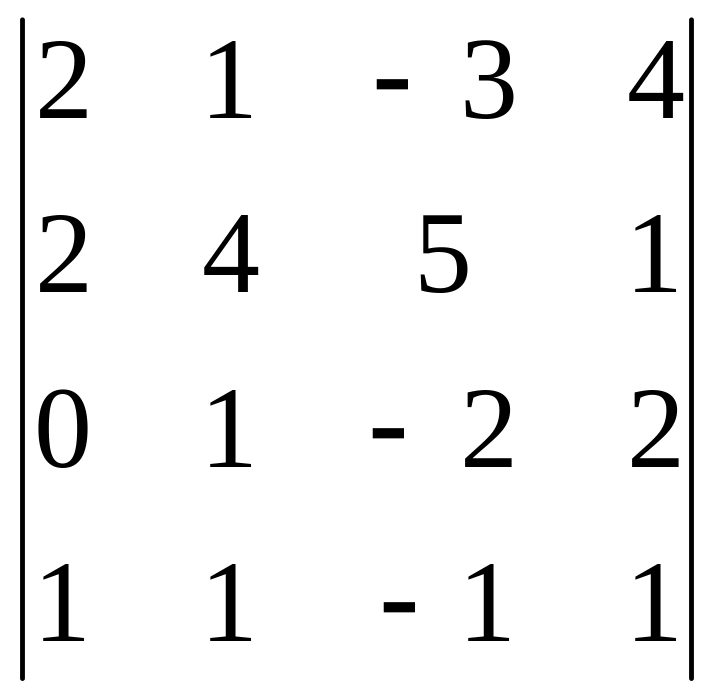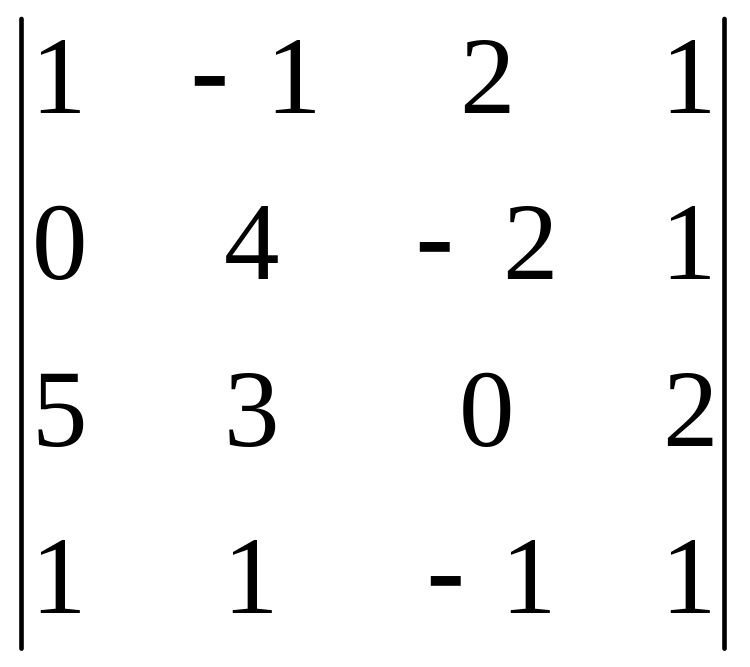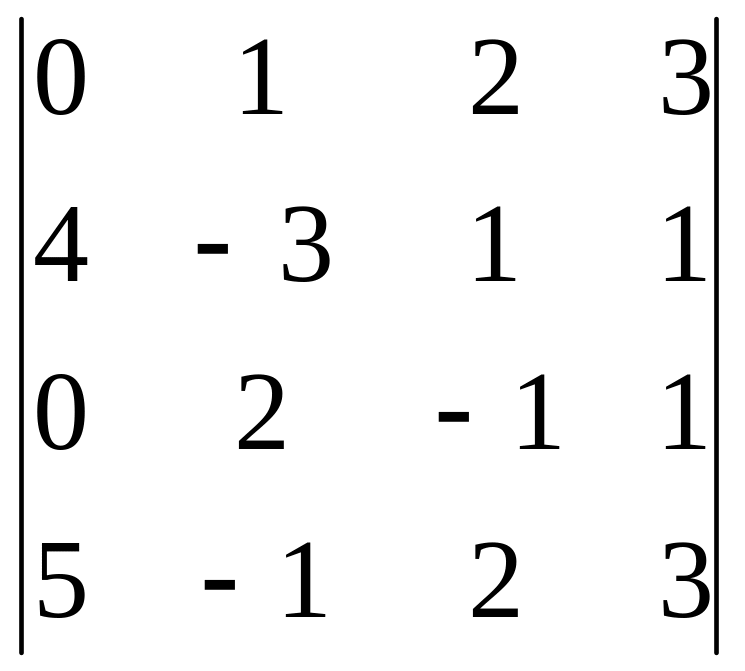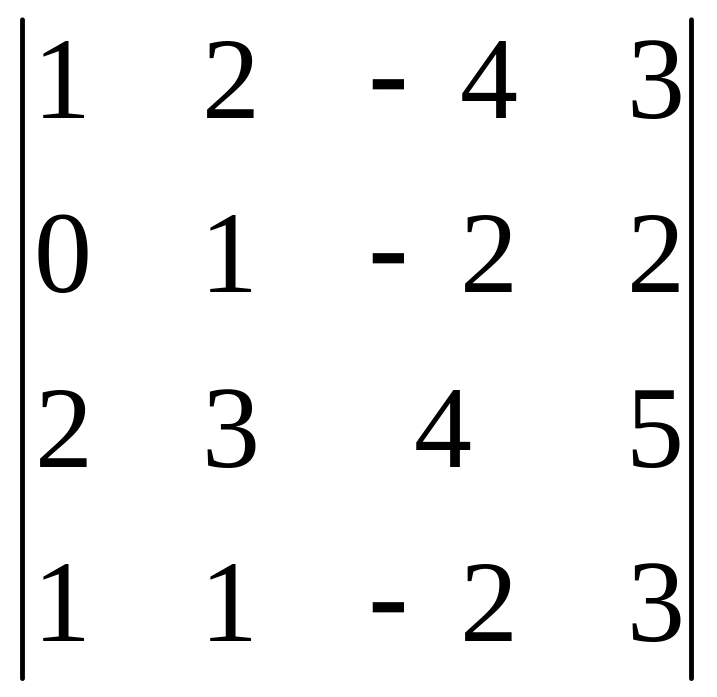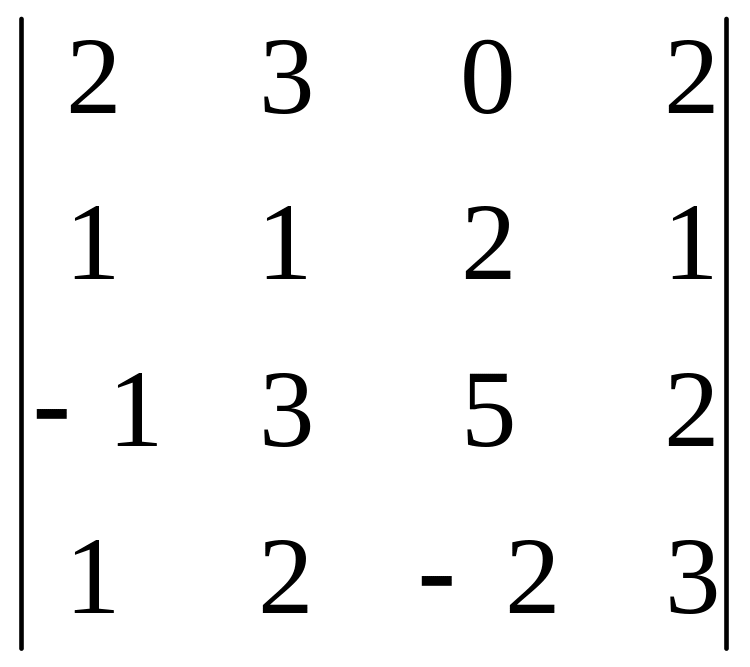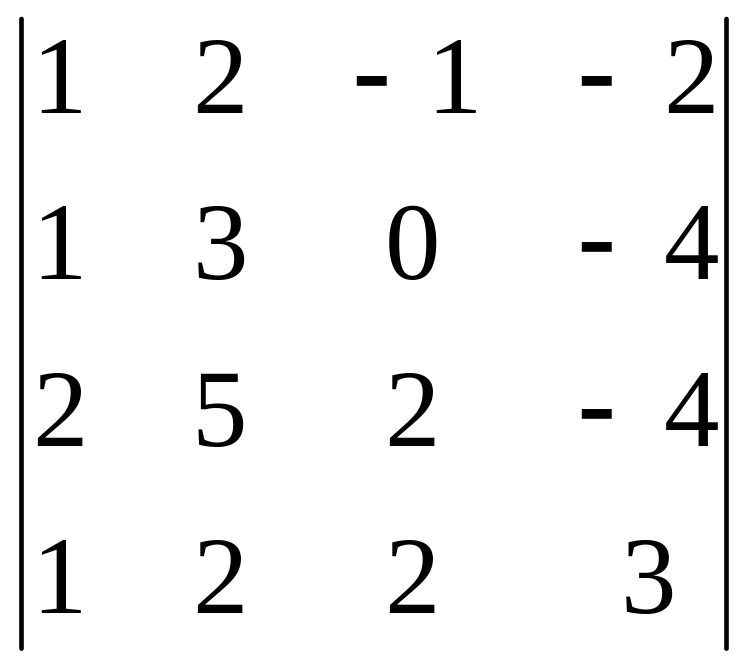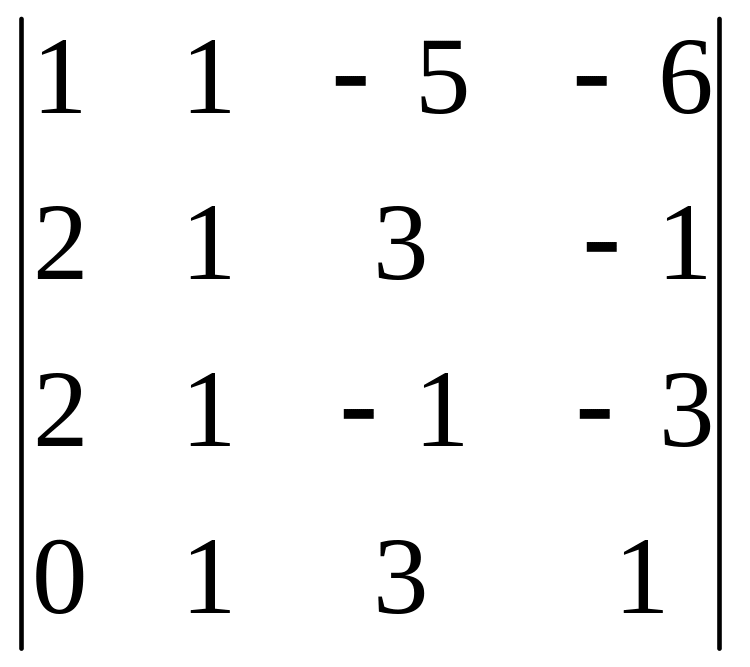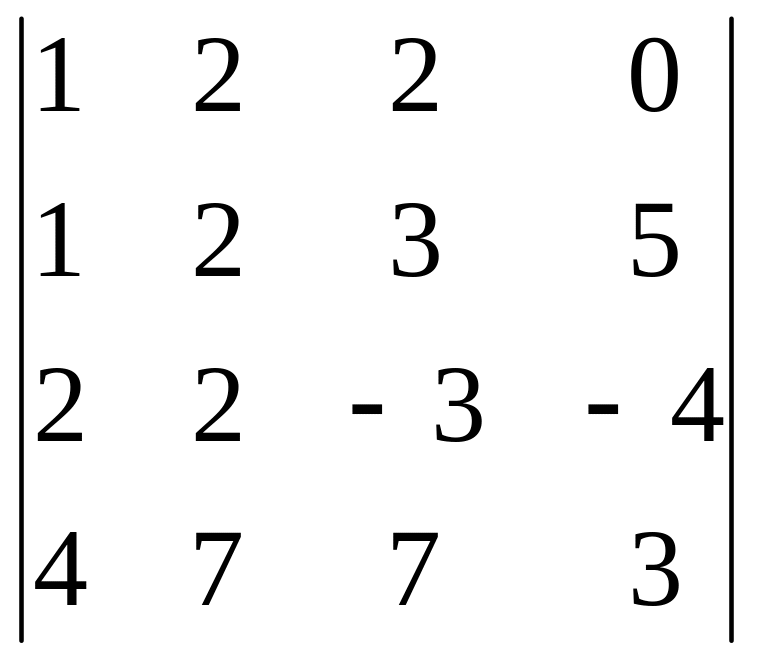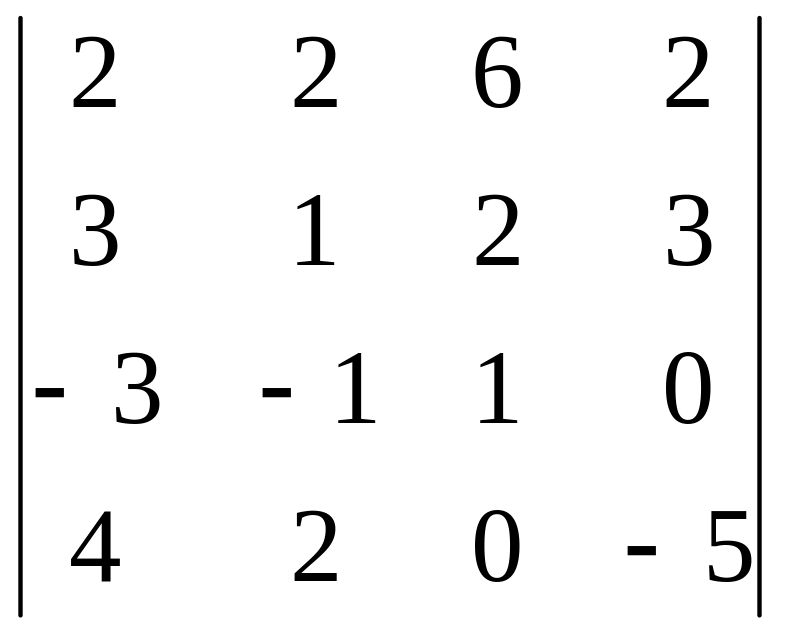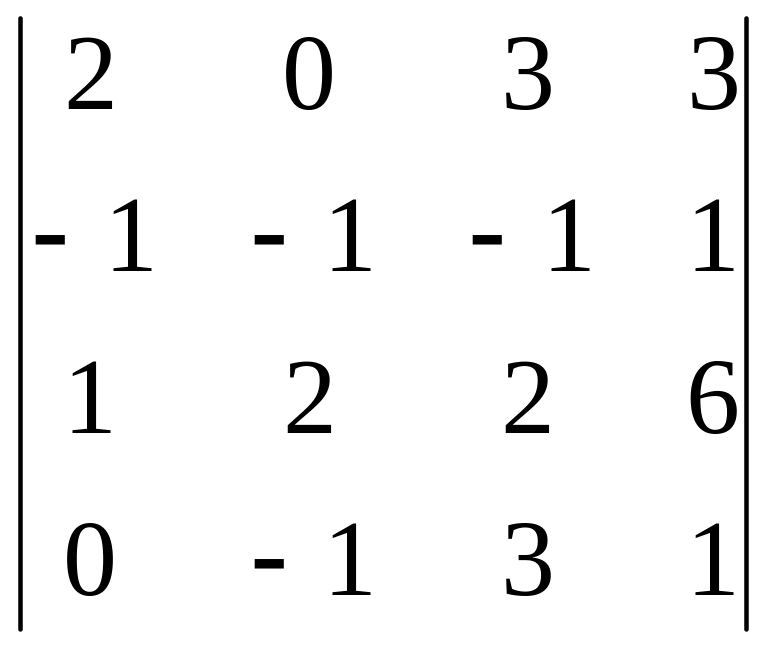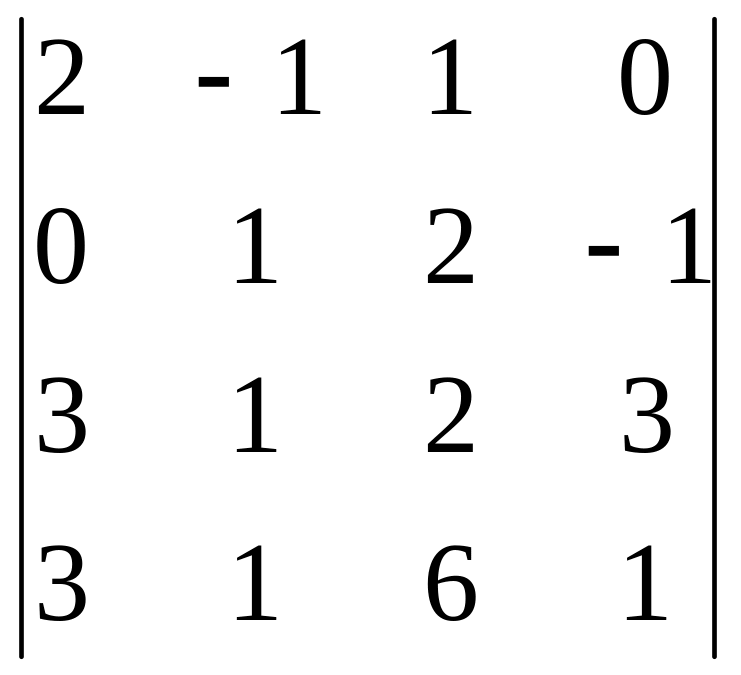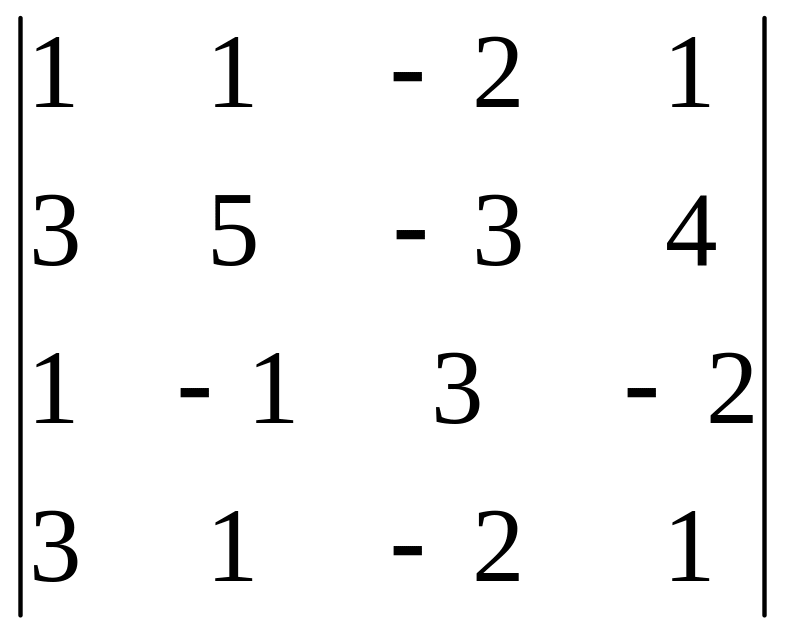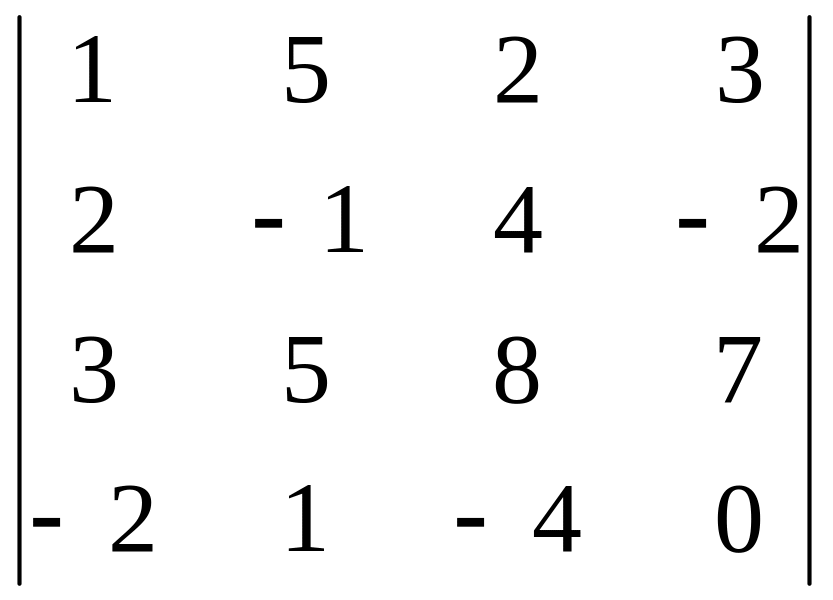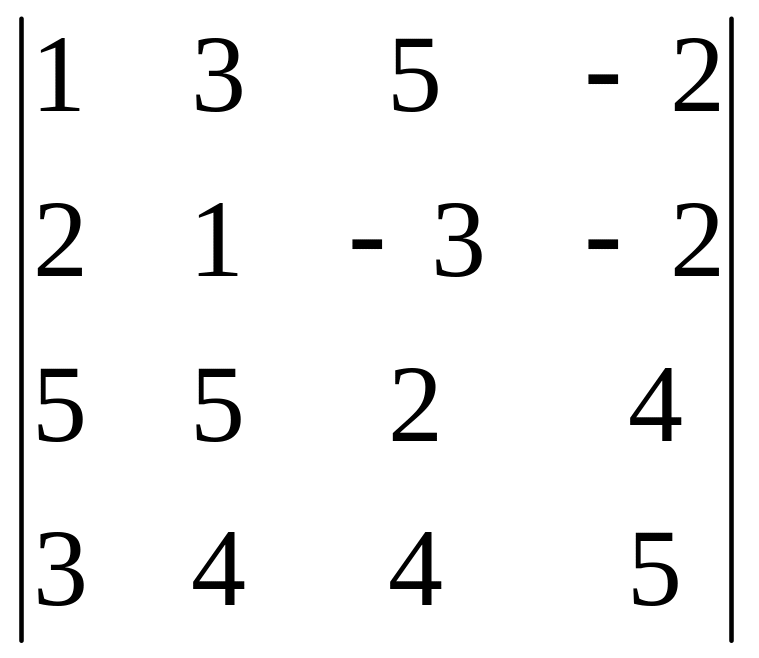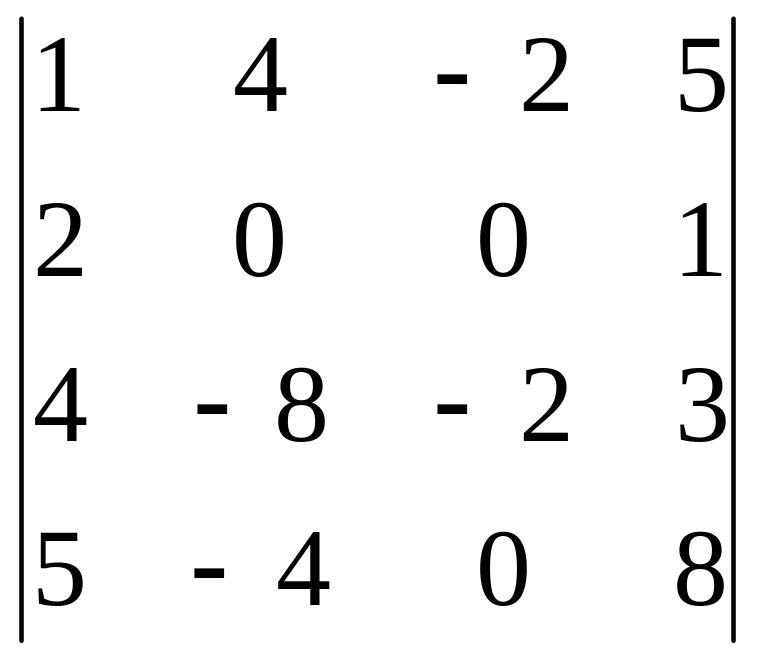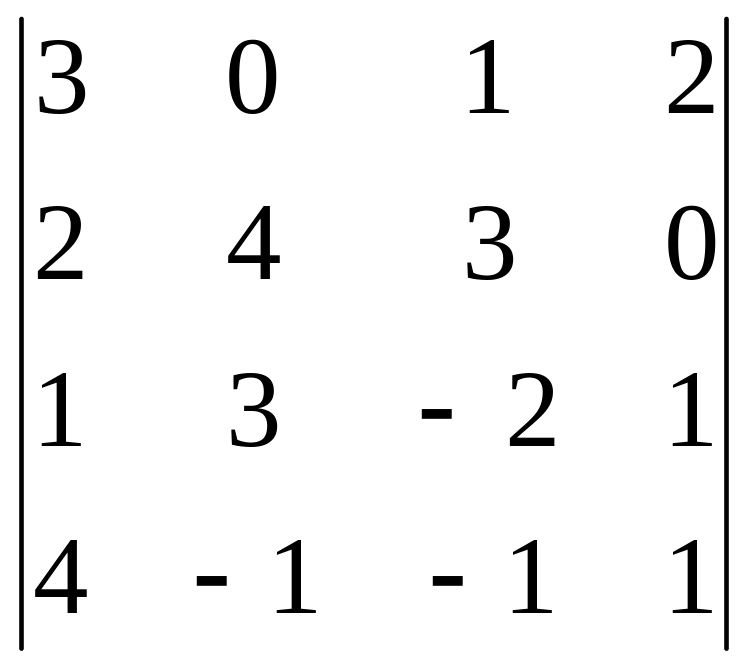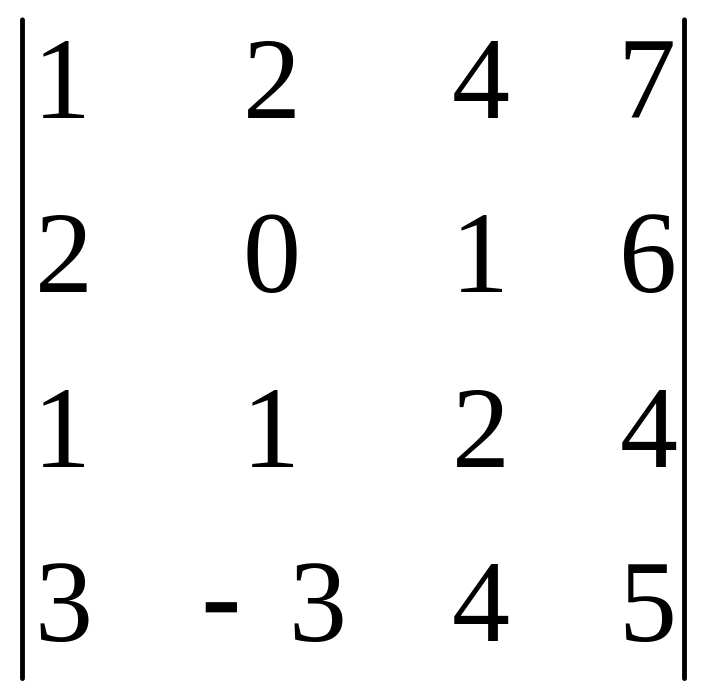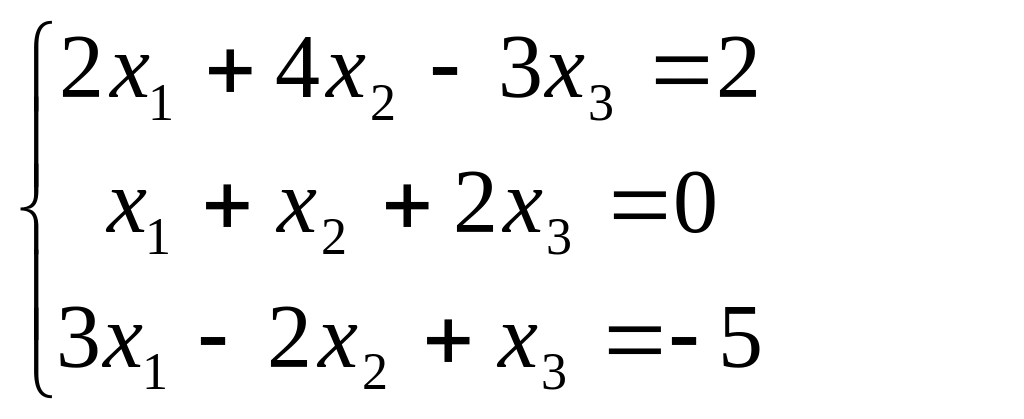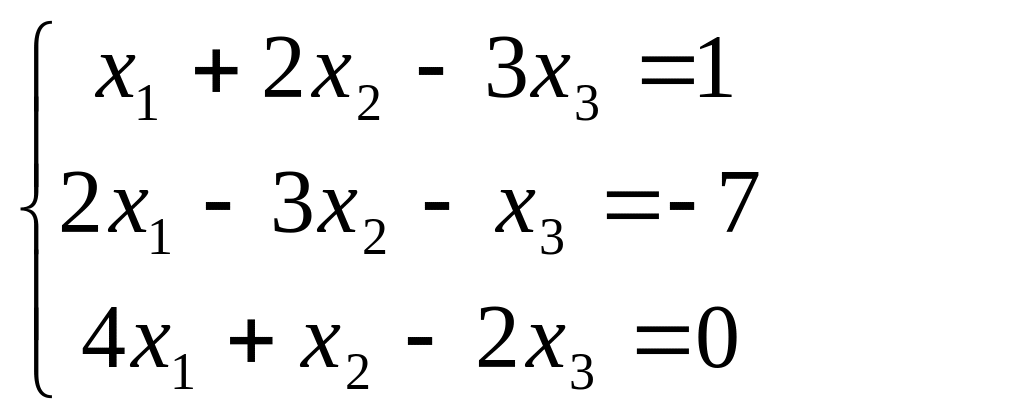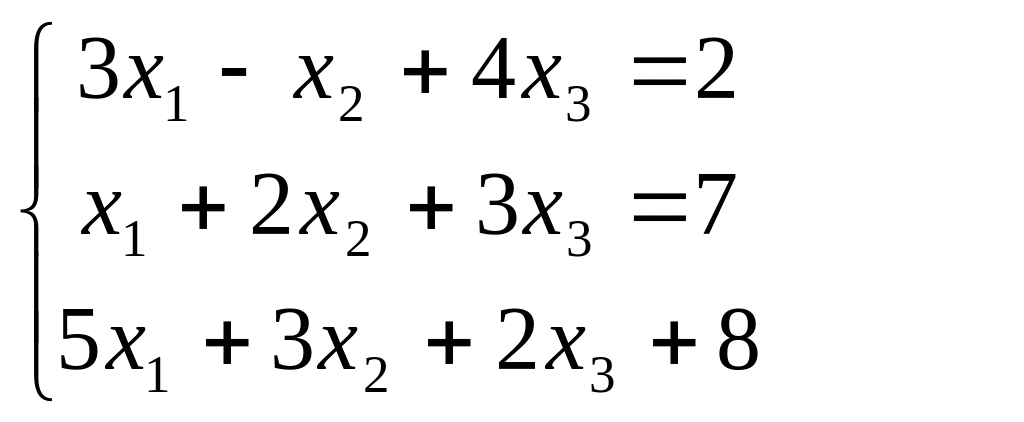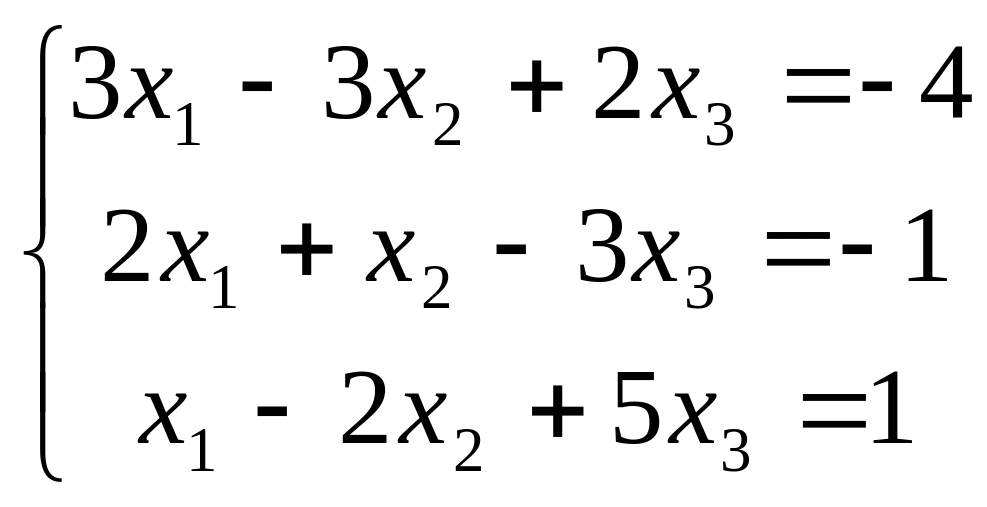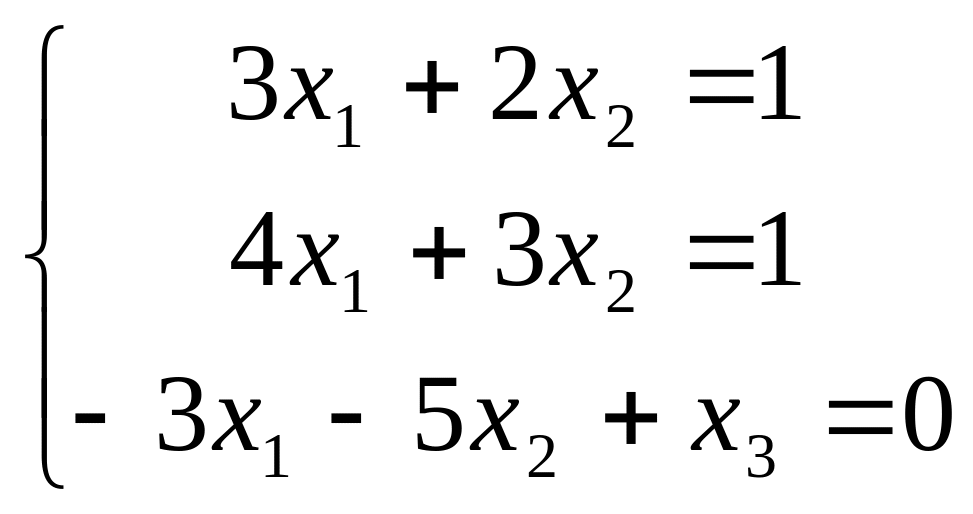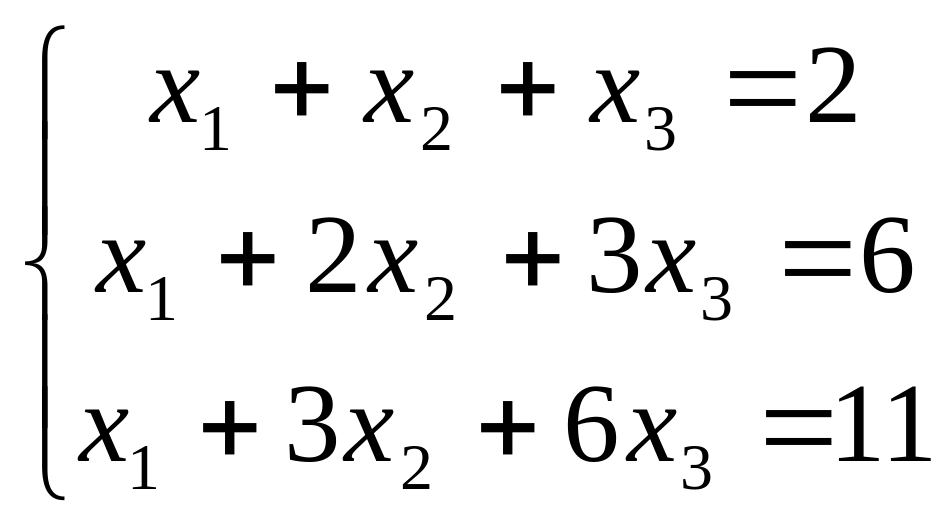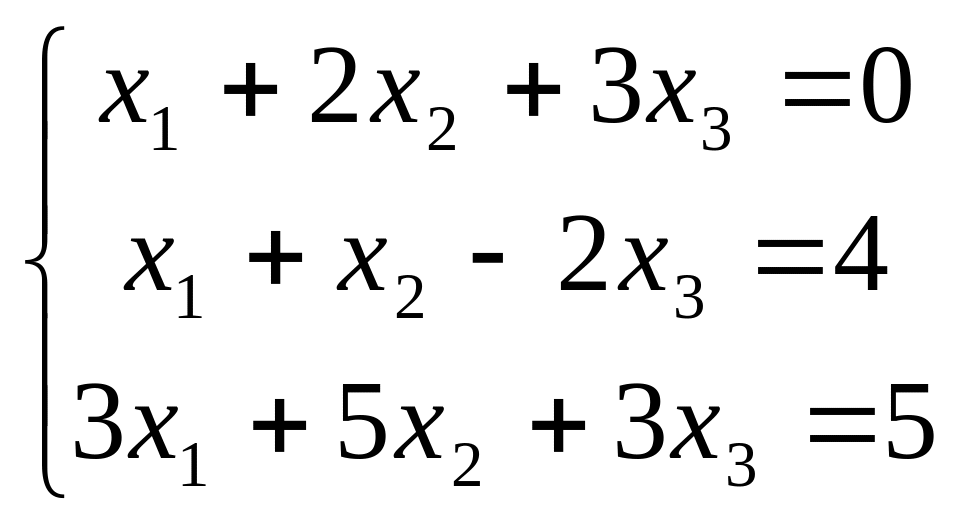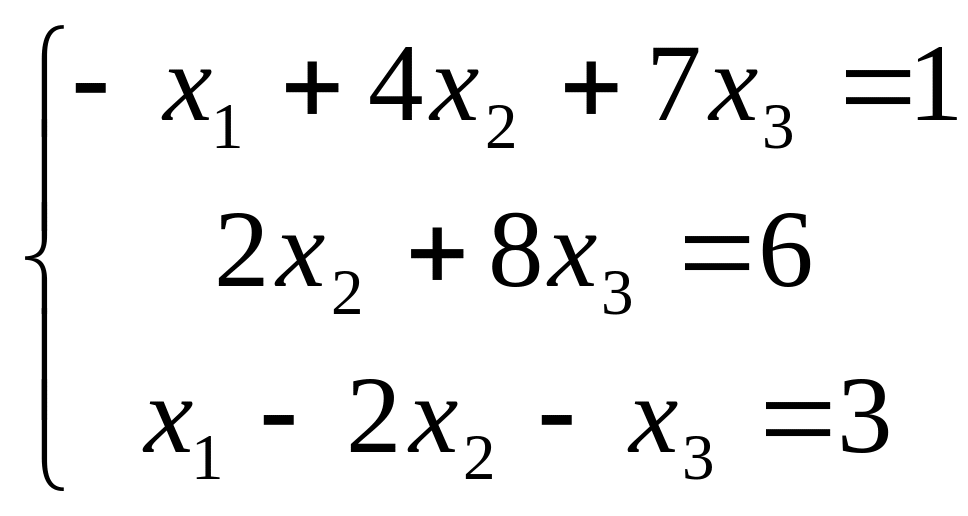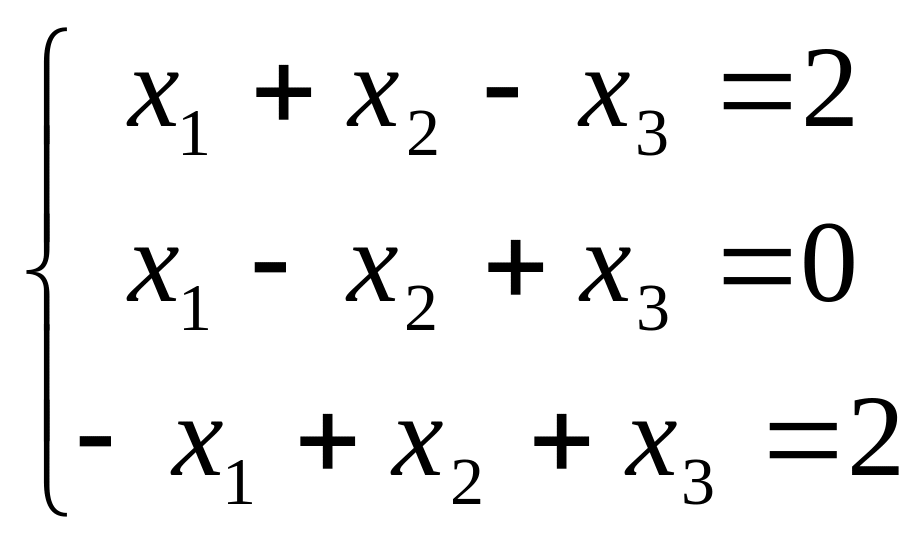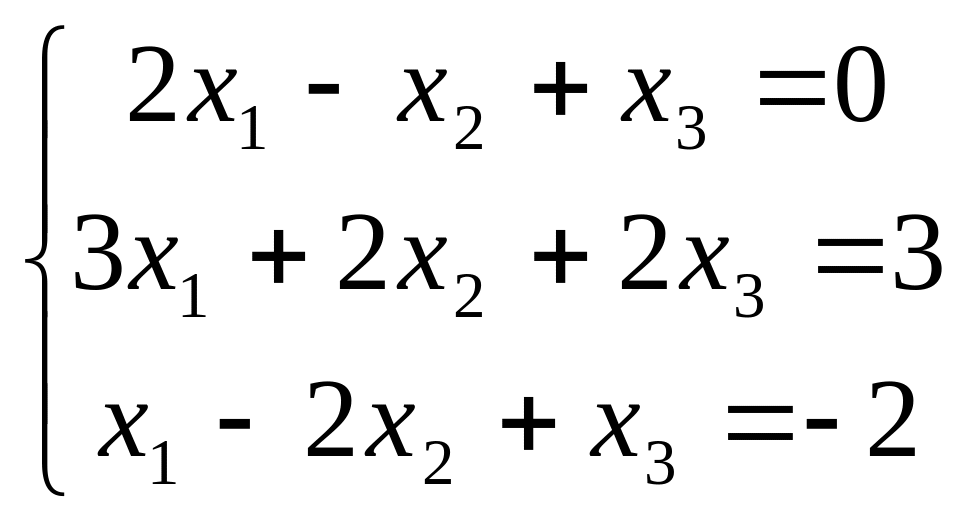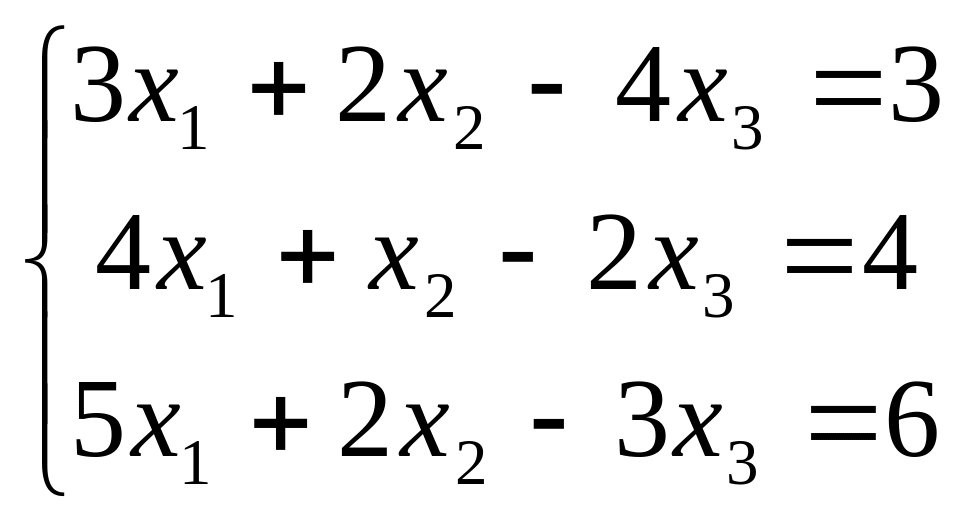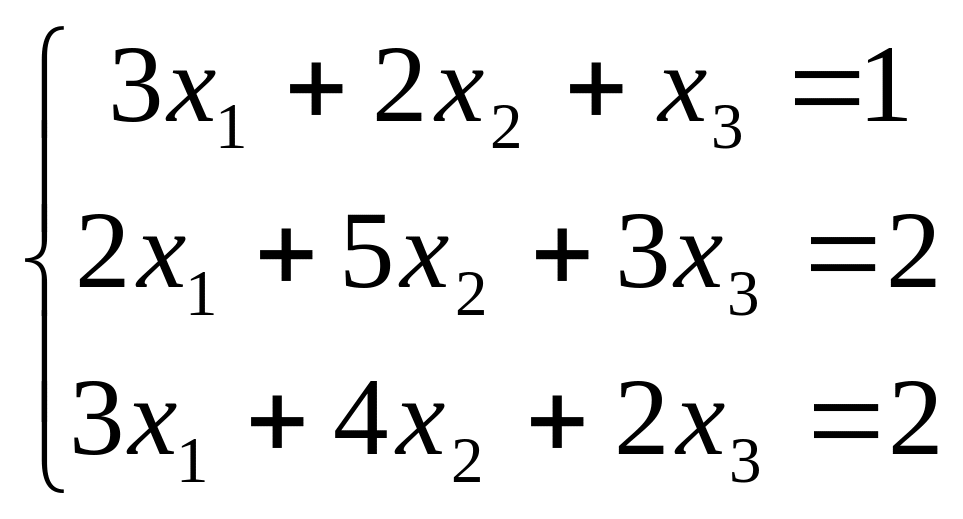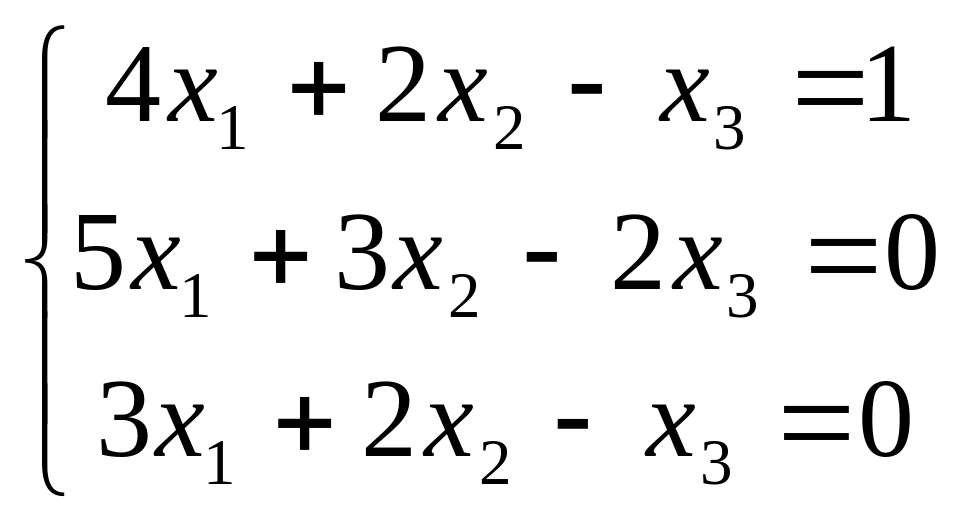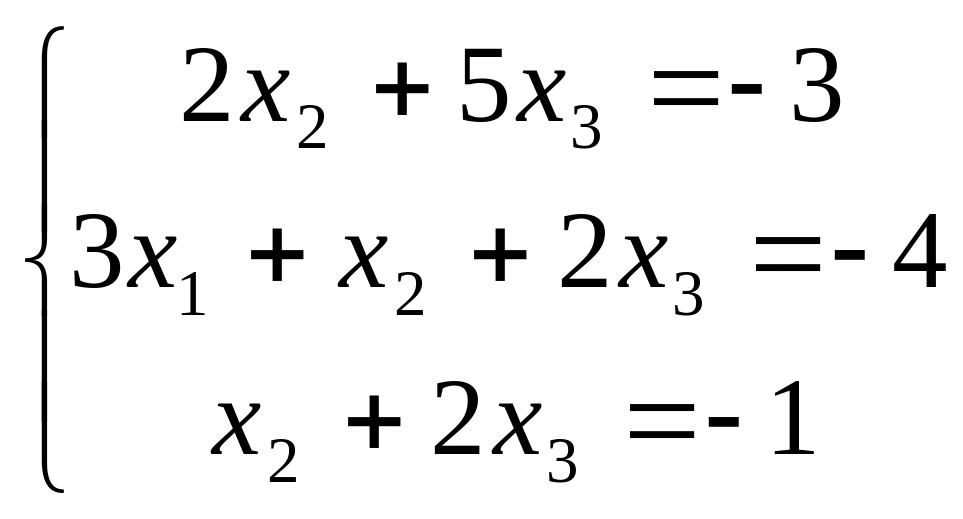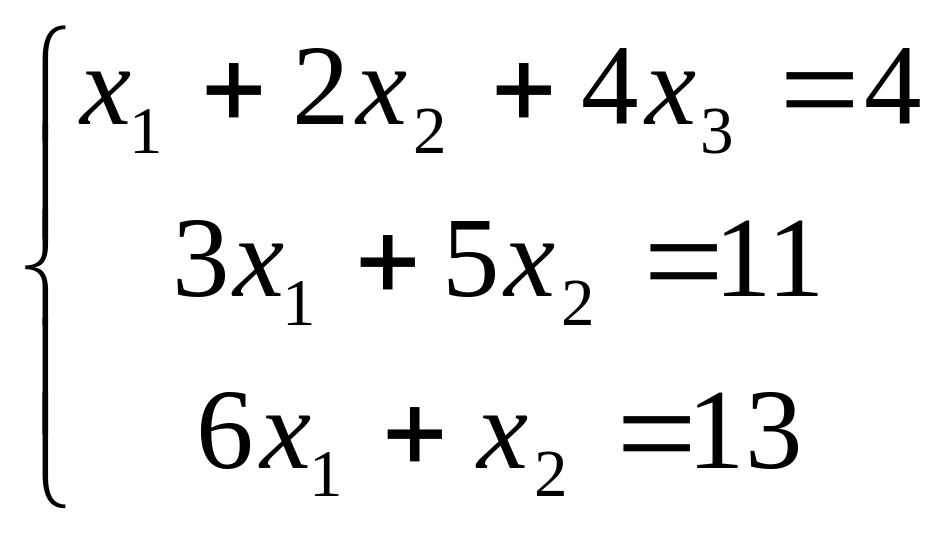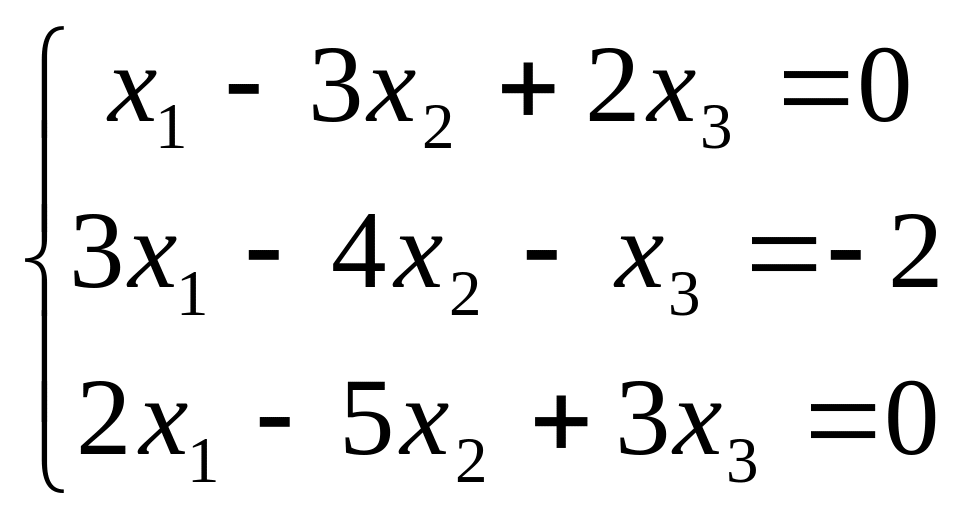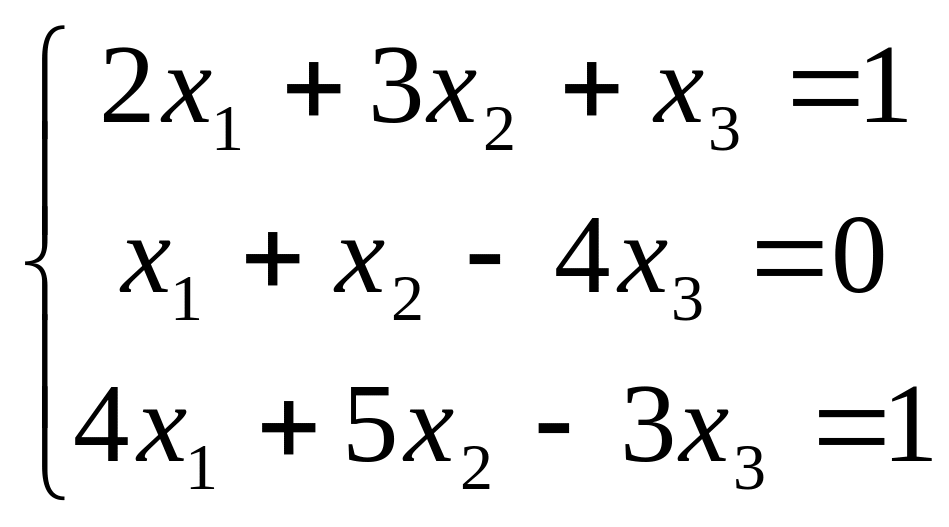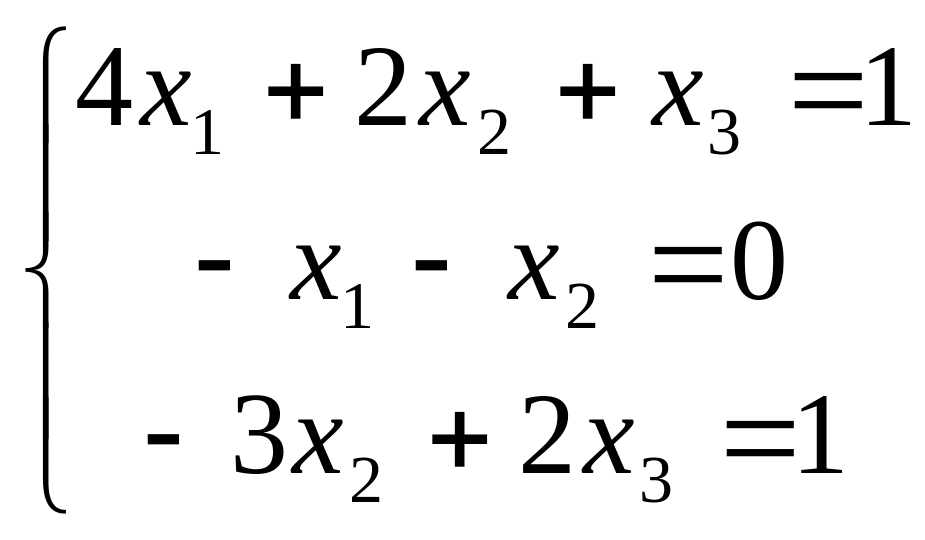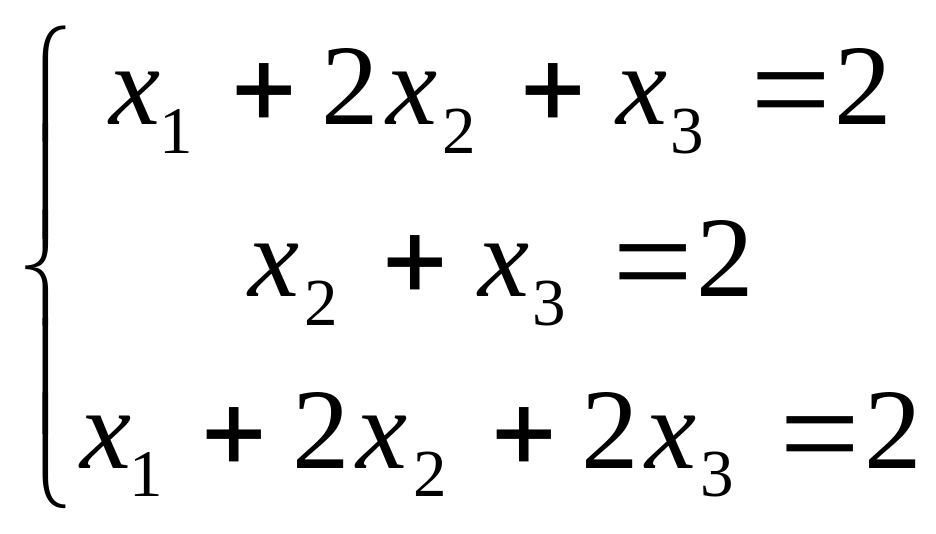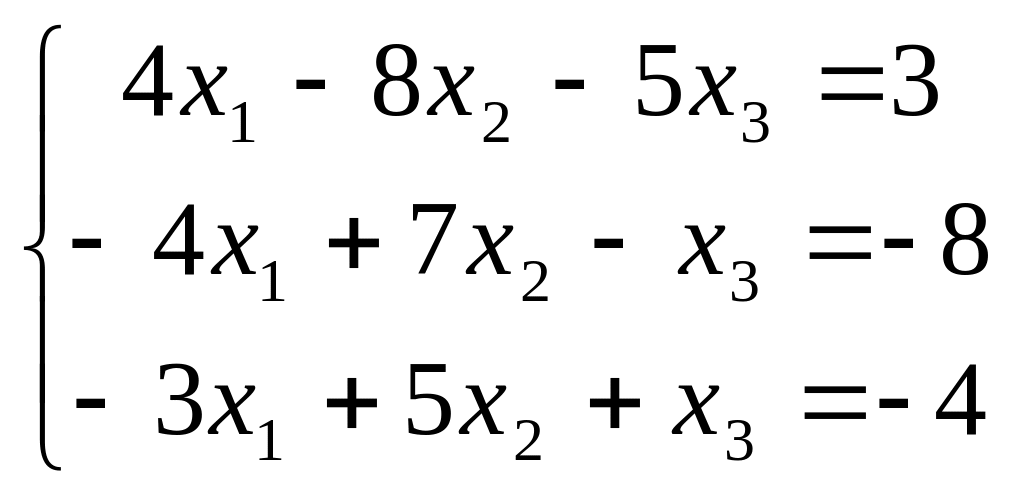Задачи для контрольной работы
В задачах 1-20 даны
вершины треугольника АВС. Найти: 1)
длину стороны АВ; 2) уравнения сторон
АВ и АС и их угловые коэффициенты;
3) внутренний угол А; 4) уравнение
высоты CD и её длину;
5) систему линейных неравенств, определяющих
![]() .
.
В задачах 21-40 определить тип кривой, привести к каноническому виду и построить кривую.
В задачах 41-49
составить уравнение линии, для каждой
точки которой отношение расстояний до
точки
![]() и до прямой
и до прямой
![]() равно числу
равно числу
![]() .
Полученное уравнение привести к
простейшему виду и построить кривую.
.
Полученное уравнение привести к
простейшему виду и построить кривую.
В задачах 50-54
составить уравнение линии, для каждой
точки которой её расстояние до точки
равно расстоянию до прямой
![]() .
Полученное уравнение привести к
каноническому виду и построить кривую.
.
Полученное уравнение привести к
каноническому виду и построить кривую.
В задачах 55-60 составить уравнение линии, используя заданные в условии соотношения для её произвольной точки. Полученное уравнение привести к каноническому виду и построить кривую.
Расстояние от каждой точки кривой до точки
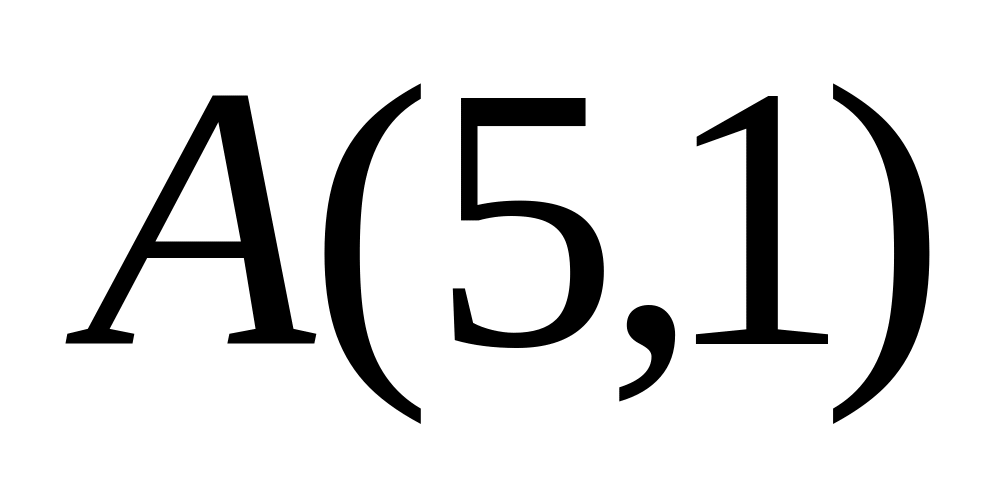 вдвое больше, чем расстояние до точки
вдвое больше, чем расстояние до точки
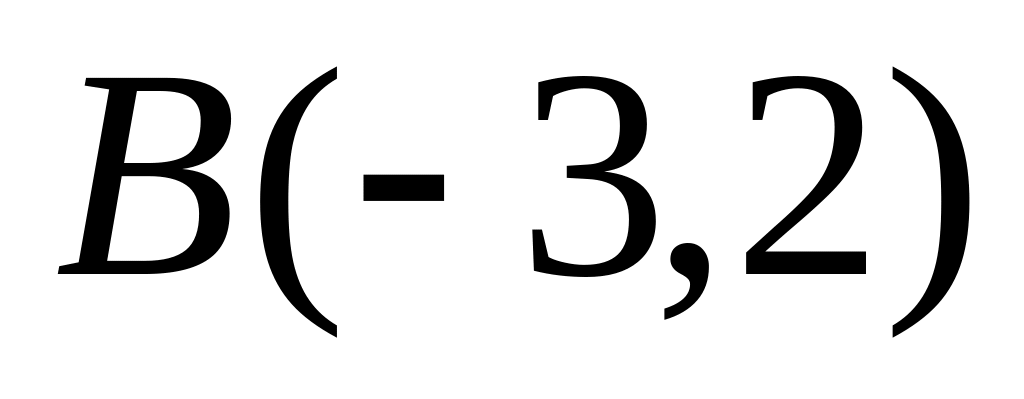 .
.Каждая точка кривой равноудалена от точек
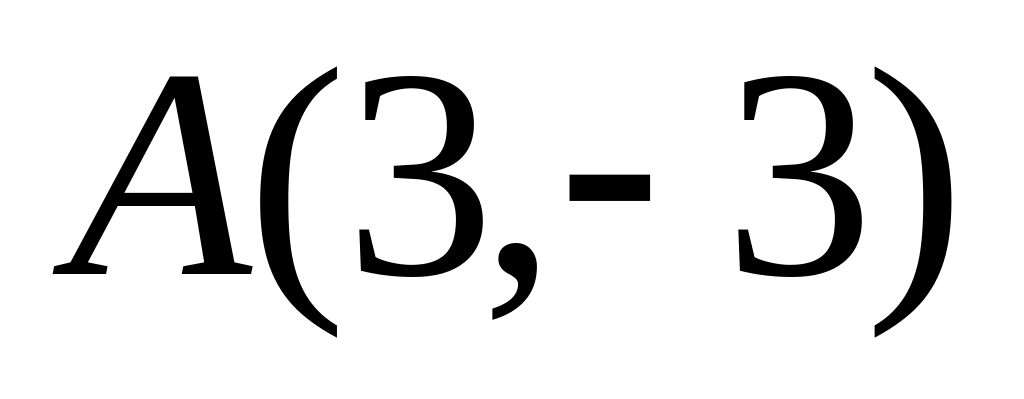 и
и
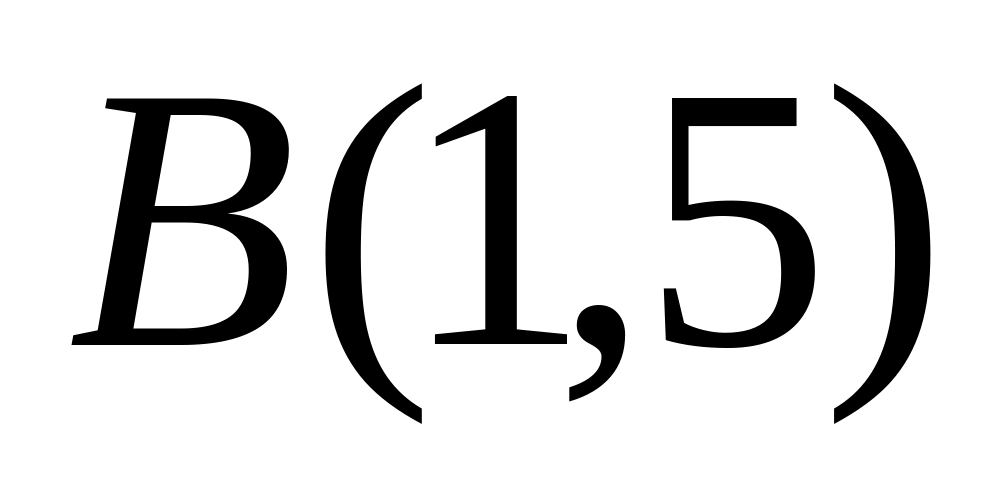 .
.Расстояние от каждой точки кривой до точек
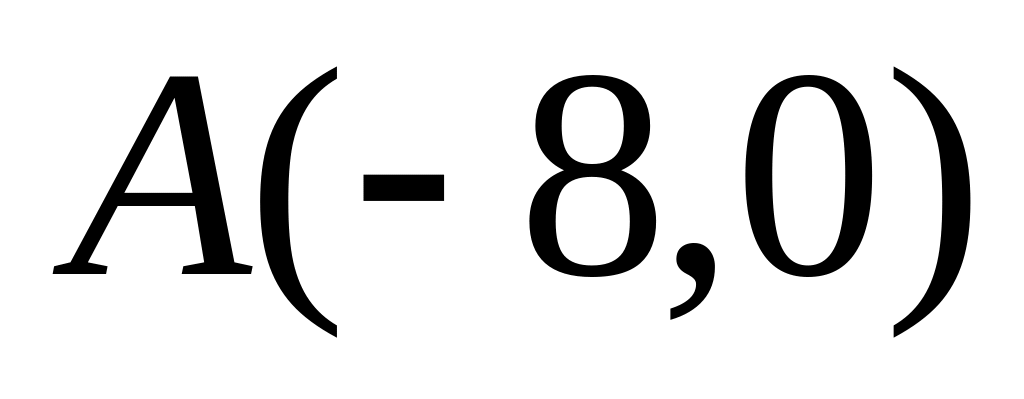 и
и
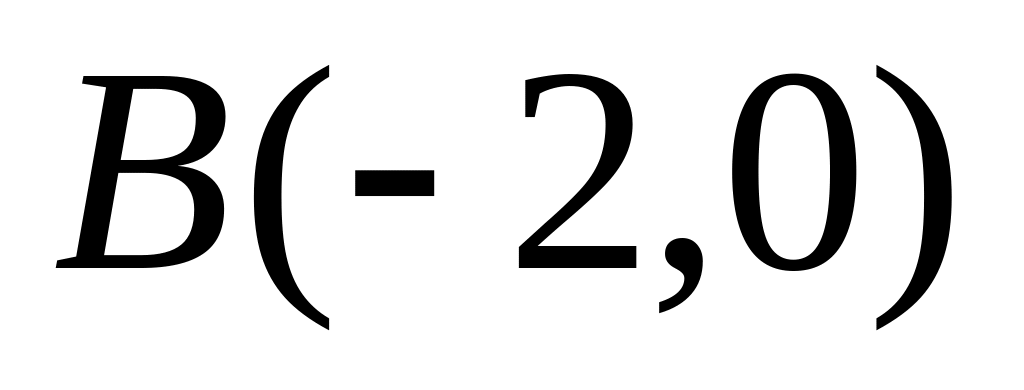 относятся как 2:1.
относятся как 2:1.Каждая точка кривой равноудалена от точек
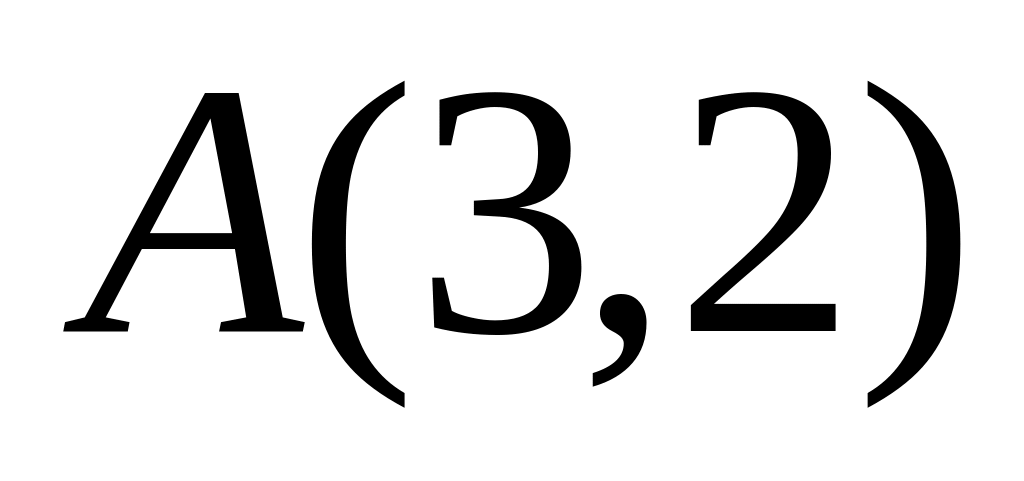 и
и
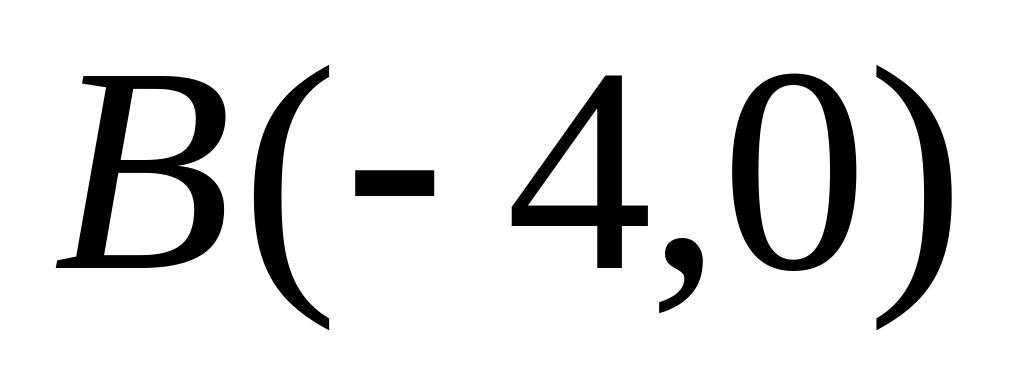 .
.Для каждой точки кривой сумма расстояний до двух данных точек
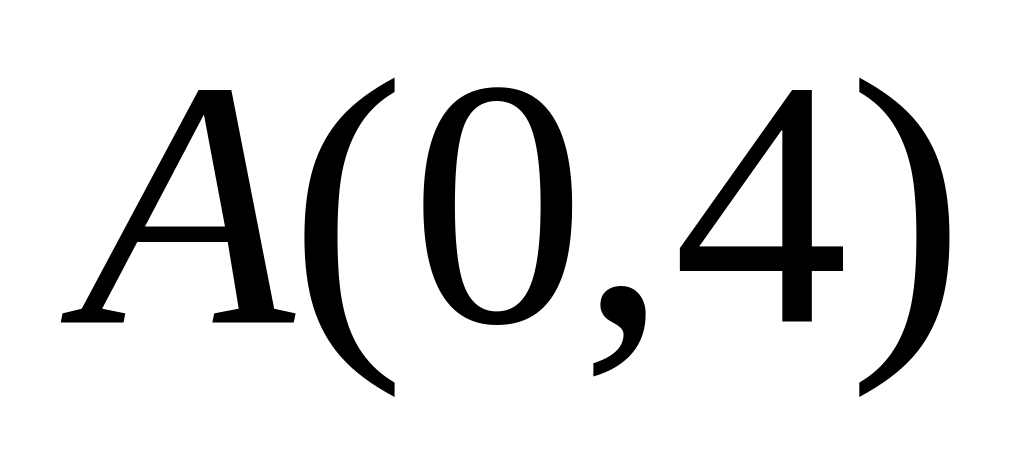 и
и
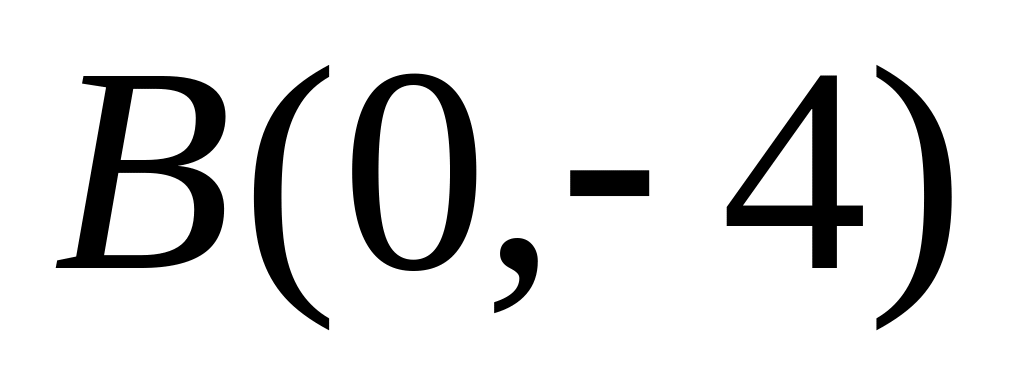 равна 10.
равна 10.Каждая точка кривой равноудалена от точки
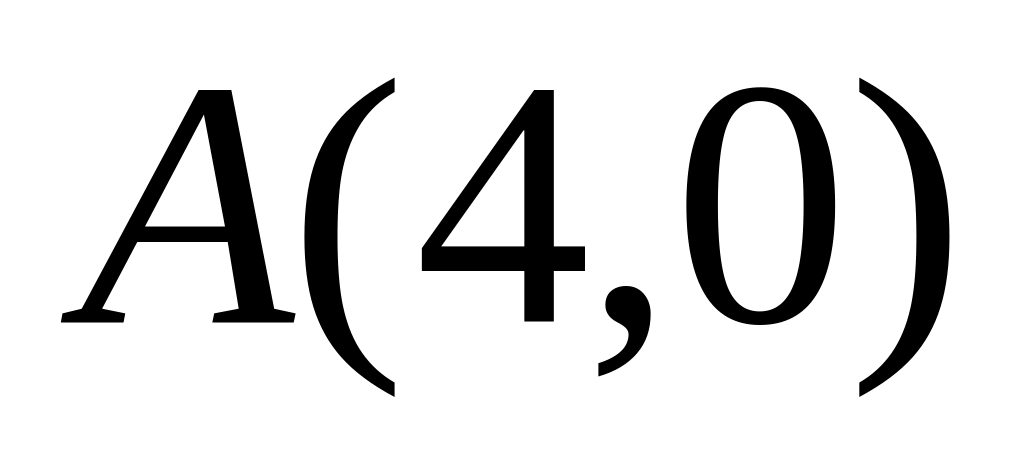 и от прямой
и от прямой
 .
.
В задачах 61-80 даны вершины треугольника АВС. Найти:
длины и уравнения сторон АВ, АС и ВС, их угловые коэффициенты;
угол между прямыми АВ и АС;
уравнение высоты СД;
уравнение медианы СЕ;
уравнение биссектрисы СК.
А (-4;2) , В (0;-1) , С (3; 3)
А (-3;-2) , В (0;-1) , С (-2; 5)
А (4;3) , В (-3;2) , С (1;-6)
А (1;2) , В (3;5) , С (5;2)
А (-2;1) , В (4;3) , С (-2;1)
А (1;-1) , В (6;4) , С (2;6)
А (2;0) , В (5;3) , С (2;6)
А (3;1) , В (4;6) , С (6;3)
А (-2;0) , В (6;6) , С (1;-4)
А (-2;1) , В (3;6) , С (5;2)
А (-2;2) , В (1;-4) , С (4;5)
А (-2;0) , В (2;6) , С (4;2)
А (-2;0) , В (2;4) , С (4;0)
А (0;7) , В (6;-1) , С (2;1)
А (-4;2) , В (2;-5) , С (5;0)
А (-3;0) , В (2;5) , С (3;2)
А (-4;-3) , В (-5;0) , С (5;6)
А (0;-4) , В (3;0) , С (0;6)
А (-4;3) , В (4;-1) , С (3;3)
А (-5;0) , В (7;9) , С (5;-5)
В задачах 81-99 даны
точки А, В, С и Д. Найти : 1) векторы
![]()
![]()
![]() ;
;
![]() =
3
=
3![]() +
1/2
+
1/2![]() ;
2) длины векторов
;
2) длины векторов
![]() .
.
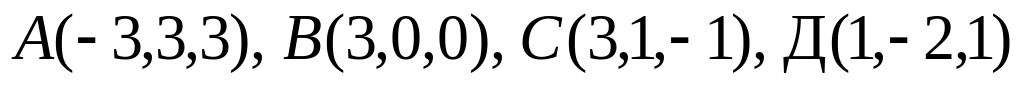
А (-2;4;4), В (4;1;1), С (4;2;0), Д (2;-1;2)
А (-5;1;1), В (1;-2;-2), С (1;-1;-3), Д (-1;-4;1)
А (0;6;6), В (6;3;3), С (6;4;2), Д (4;1;4)
А (-2;1;1), В (0;-3;-3), С (0;-2;-4), Д (-2;-5;-2)
А (-1;2;1), В (1;-2;-3), С (1;-1;-4), Д (-1;-4;-2)
А (1;2;2), В (3;-2;-2), С (3;-1;-3), Д (1;-4;-1)
А (-2;2;2), В (0;-2;-2), С (0;-1;-3), Д (-2;-4;-1)
А (-2;2;1), В (0;-2;-3), С (0;-1;-4), Д (-2;-4;-2)
А (-2;1;2), В (0;-3;-2), С (0;-2;-3), Д (-2;-5;-1)
А (1;2;-1), В (3;-2;3), С (1;1;1), Д (2;3;1)
А (3;1;2), В (5;-3;6), С (3;0;4), Д (4;2;4)
А (3;-2;3), В (1;2;-1), С (1;1;-3), Д (2;3;1)
А (2;3;1), В (6;2;0), С (4;2;1), Д (4;6;0)
А (3;1;0), В (4;3;-2), С (5;2;2), Д (4;2;3)
А (2;-3;0), В (4;-2;2), С (3;-1;-2), Д (4;-5;-1)
А (2;0;-2), В (0;-3;0), С (2;-1;-1), Д (-4;2;2)
А (3;0;0), В (3;1;-1), С (1;-2;1), Д (-3;3;3)
А (4;1;1), В (4;2;0), С (2;-1;2), Д (-2;4;4)
Задачи
100-120. В пирамиде
![]() даны декартовы координаты точек вершин
даны декартовы координаты точек вершин
![]() .
Найти: 1) координаты векторов
.
Найти: 1) координаты векторов
![]() ;
2) определить длины рёбер
;
3) найти угол между рёбрами
и
;
4) вычислить площадь грани
;
5) вычислить объём пирамиды
.
;
2) определить длины рёбер
;
3) найти угол между рёбрами
и
;
4) вычислить площадь грани
;
5) вычислить объём пирамиды
.
Задачи 121-140. Даны
векторы
![]() .
Показать, что векторы
образуют базис и найти координаты
вектора
в этом базисе.
.
Показать, что векторы
образуют базис и найти координаты
вектора
в этом базисе.
В
задачах 141-160 даны координаты трёх точек
![]() .
Требуется: 1) записать векторы
и
в системе орт; 2) найти площадь треугольника,
построенного на векторах
и
.
.
Требуется: 1) записать векторы
и
в системе орт; 2) найти площадь треугольника,
построенного на векторах
и
.
В задачах 161-180 дан определитель D.
Записать разложение определителя по какой-либо строке или столбцу.
Вычислить определитель, получив предварительно нули в какой-либо строке или столбце.
В задачах 181-200 дана система линейных уравнений. Решить её методом Крамера, матричным способом, методом Гаусса
В задачах 201-220 даны матрицы А и В.
а) найти матрицу
![]()
в) решить матричное уравнение AX=B
А=
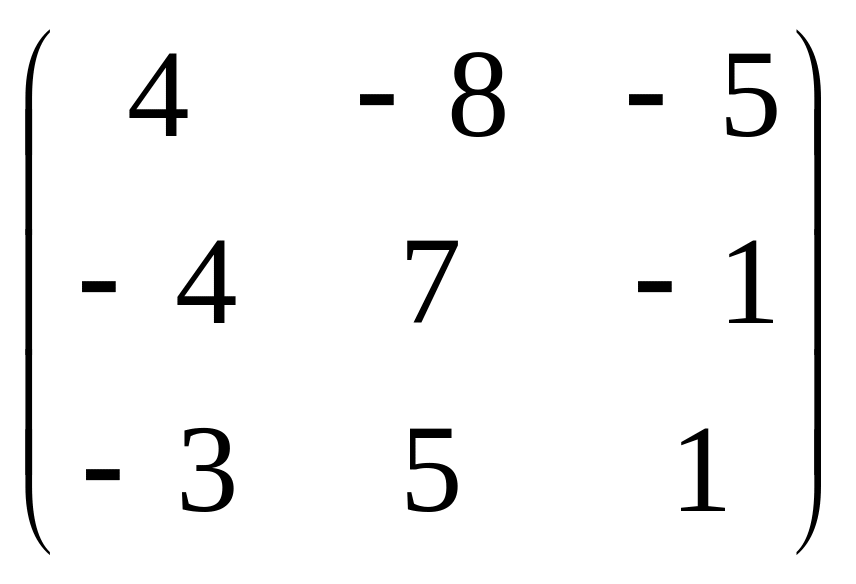 ;
В =
;
В =
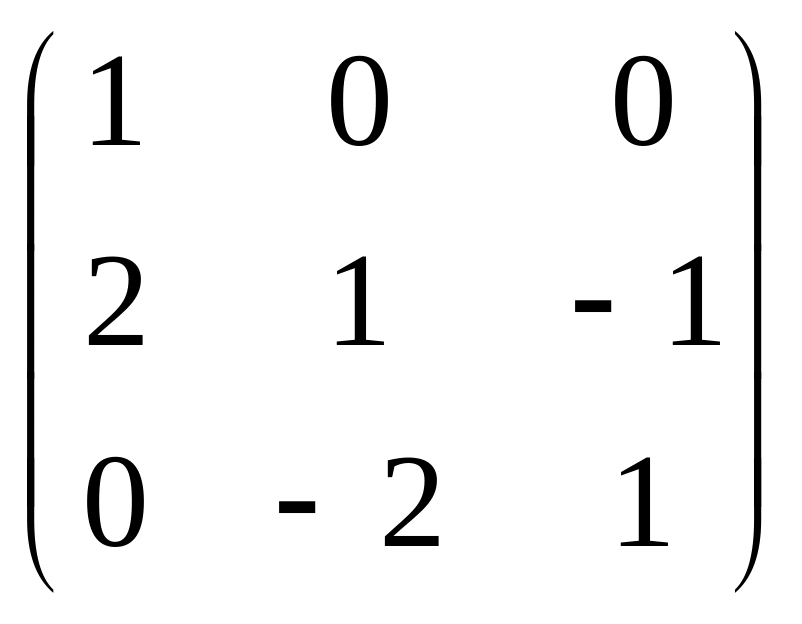
А =
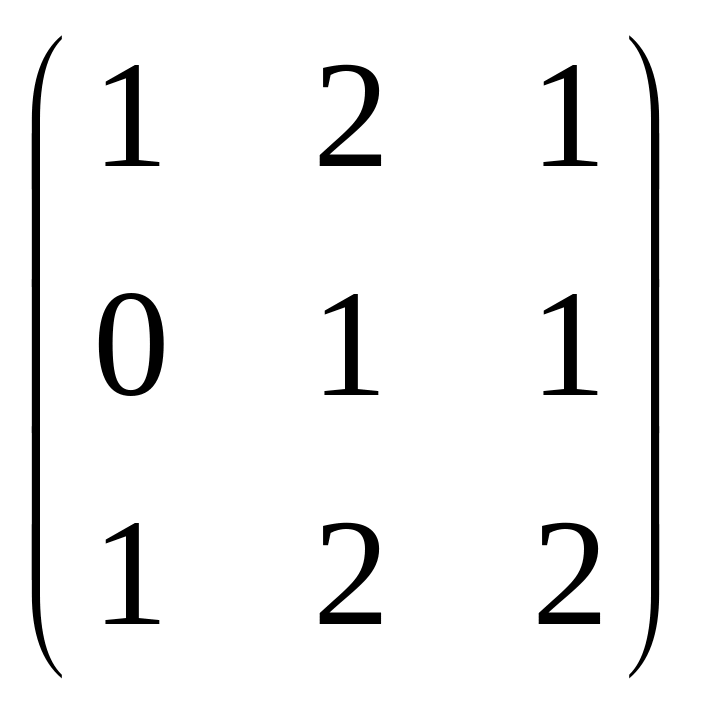 ;
В =
;
В =
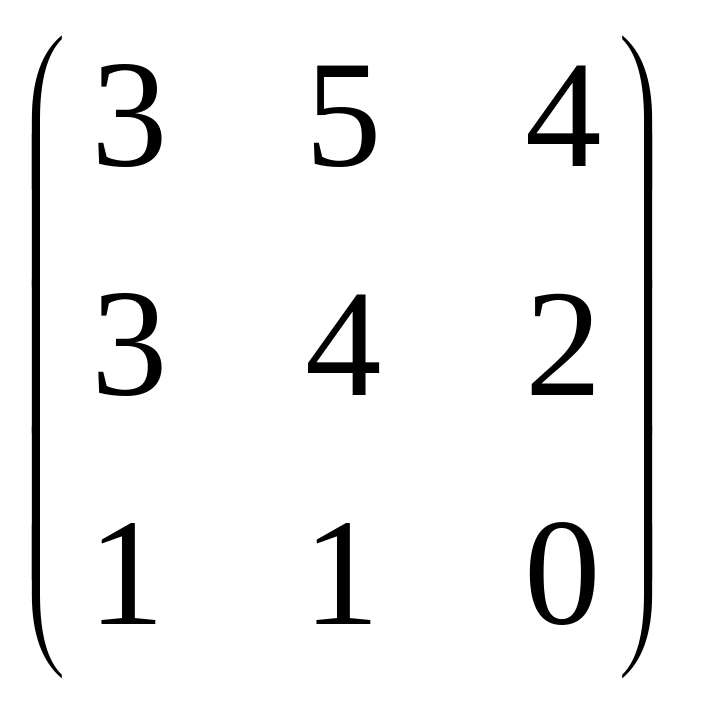
А=
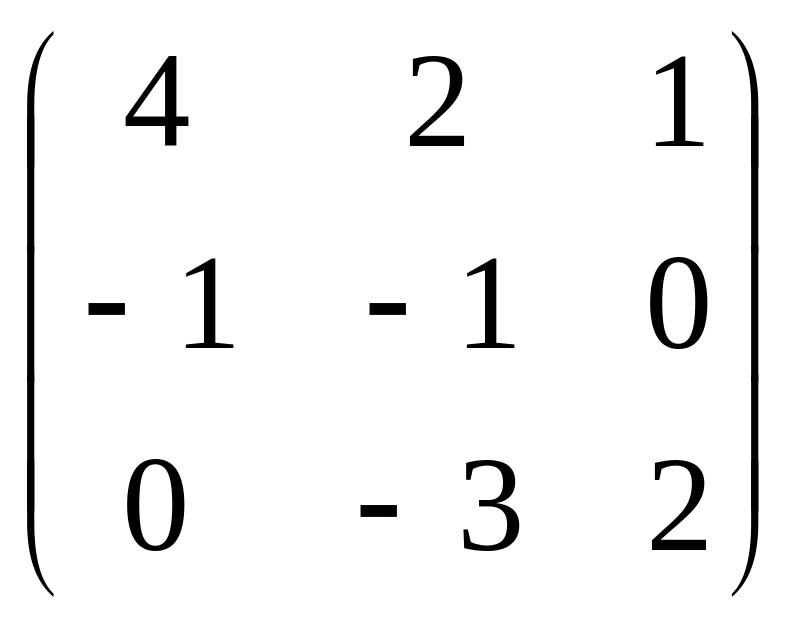 ;
В =
;
В =
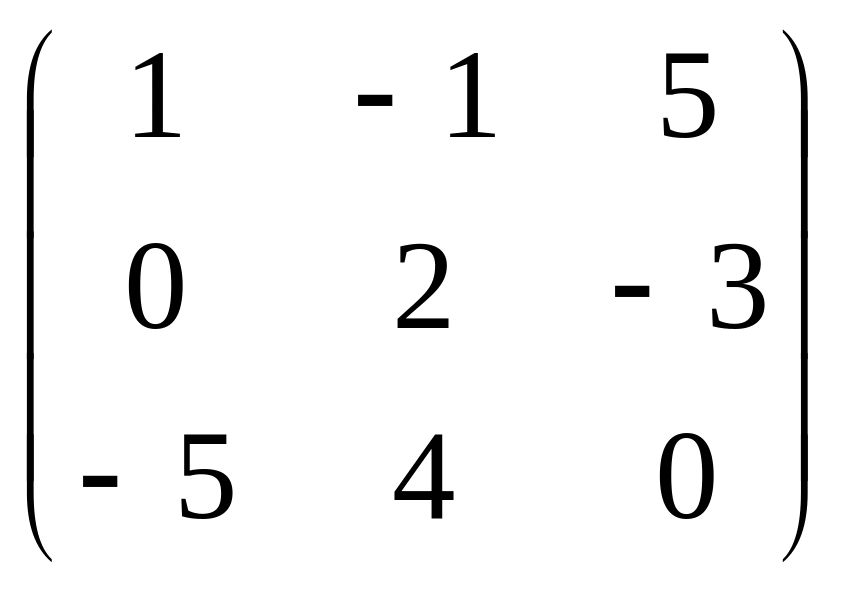
А =
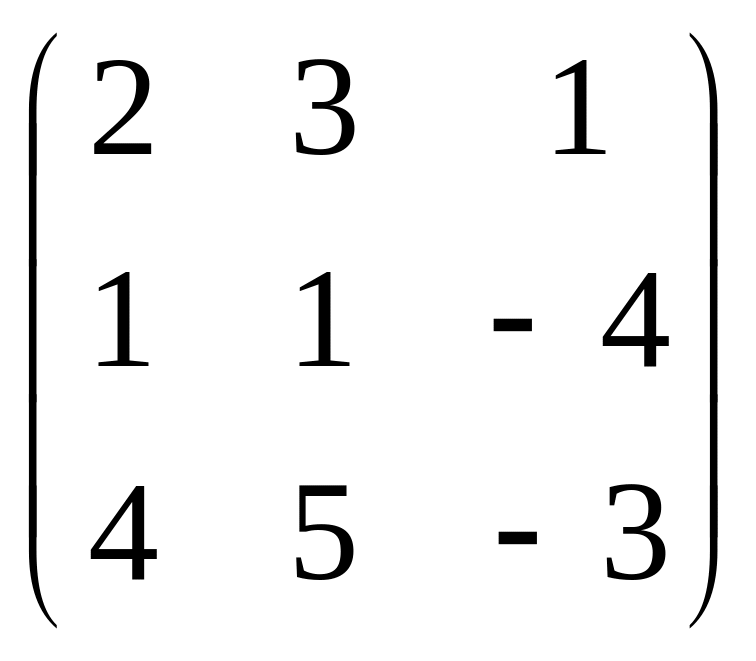 ;
В =
;
В =
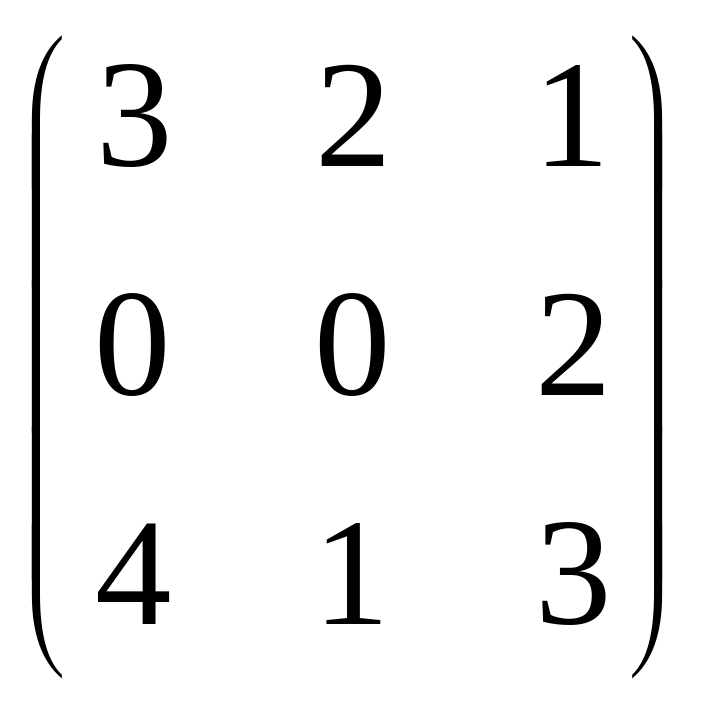
А =
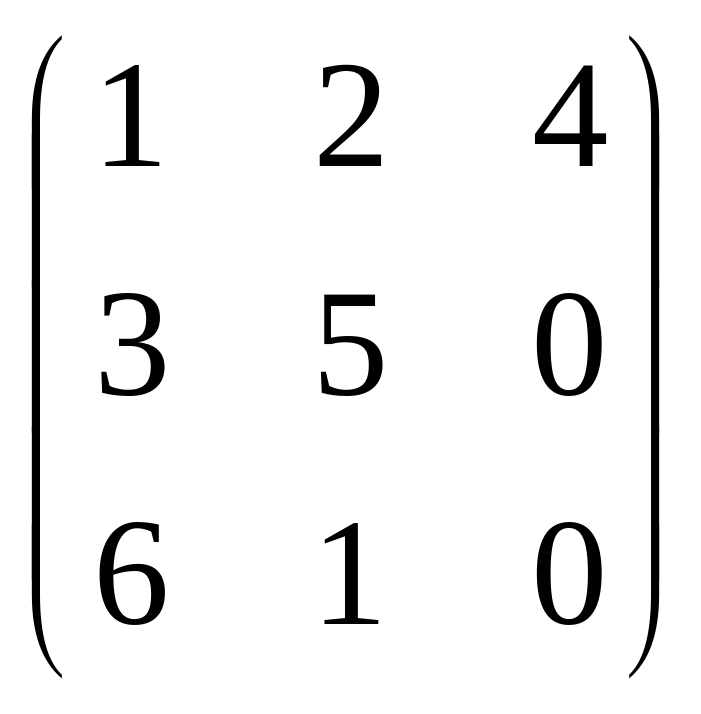 ;
В =
;
В =
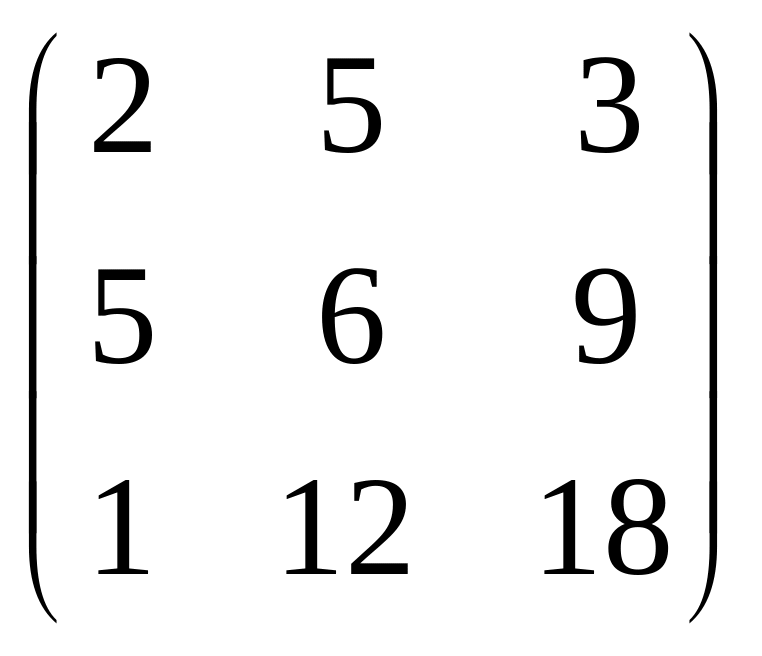
А =
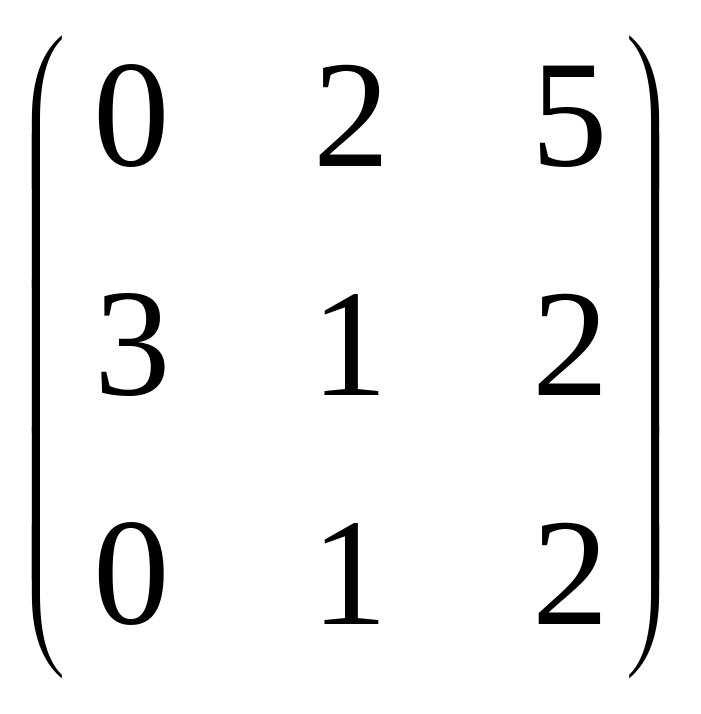 ;
В =
;
В =
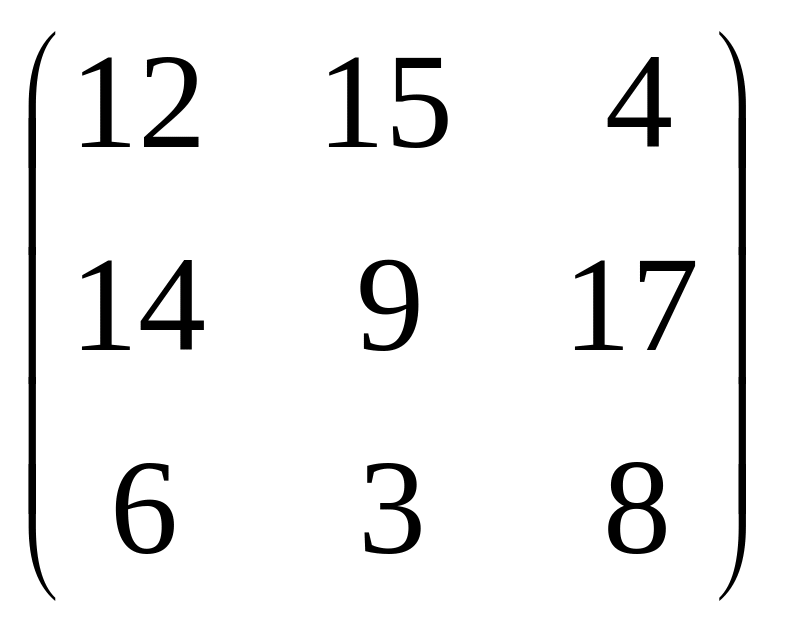
А =
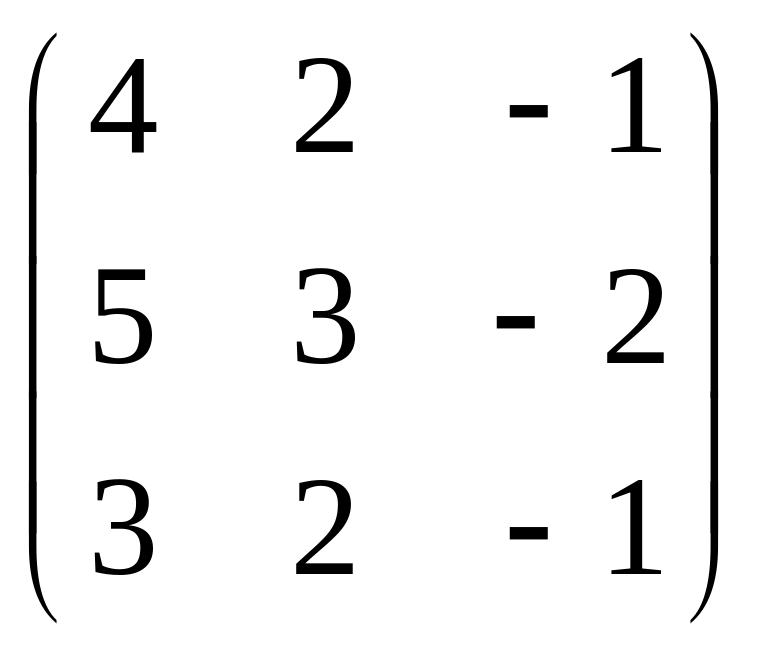 ;
В =
;
В =
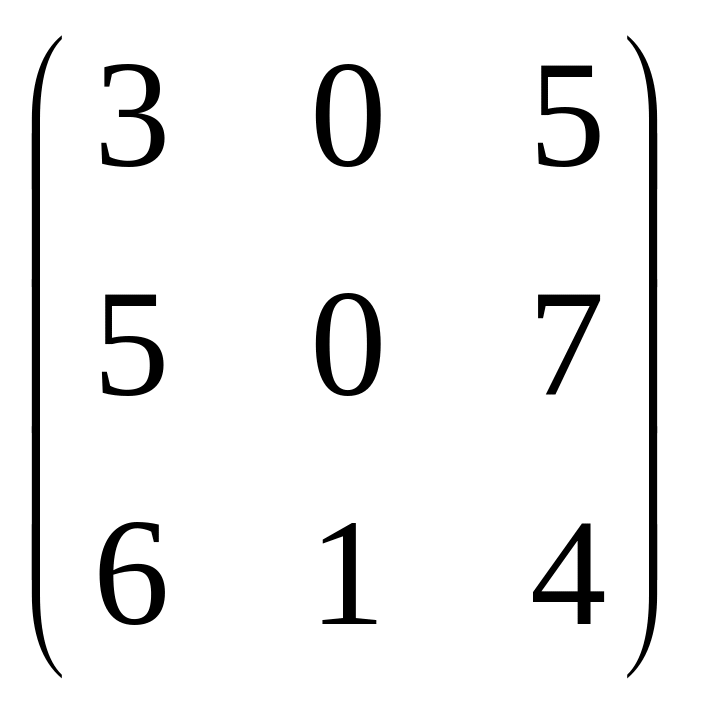
А =
 ;
В =
;
В =

А=
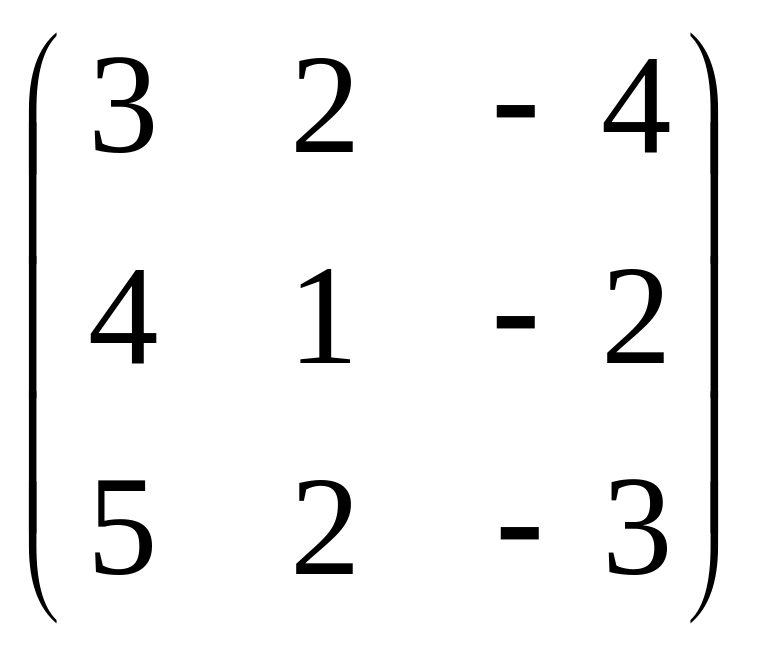 ;
В =
;
В =
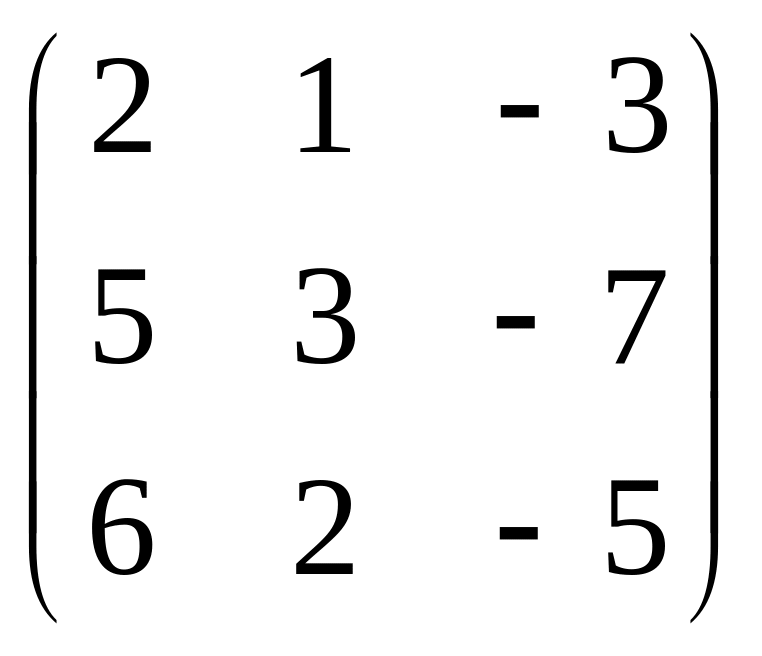
А=
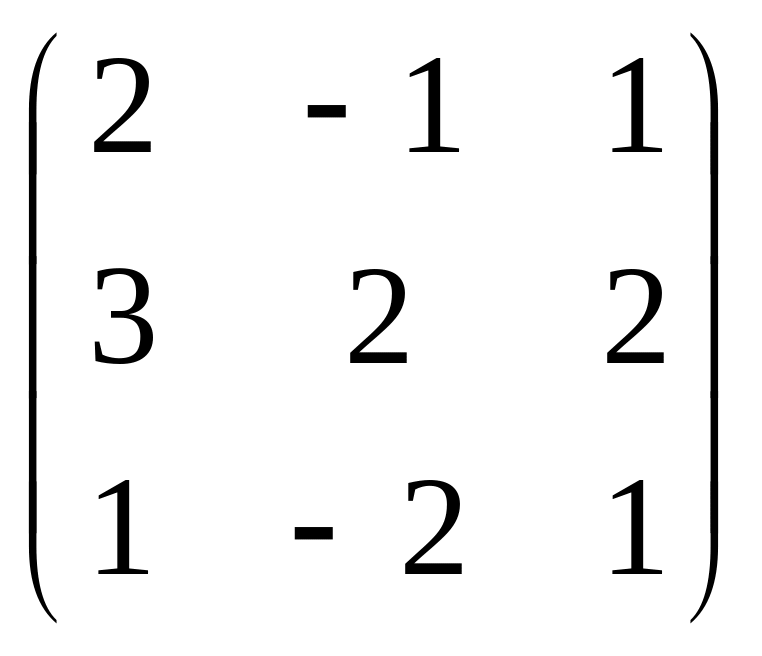 ;
В =
;
В =
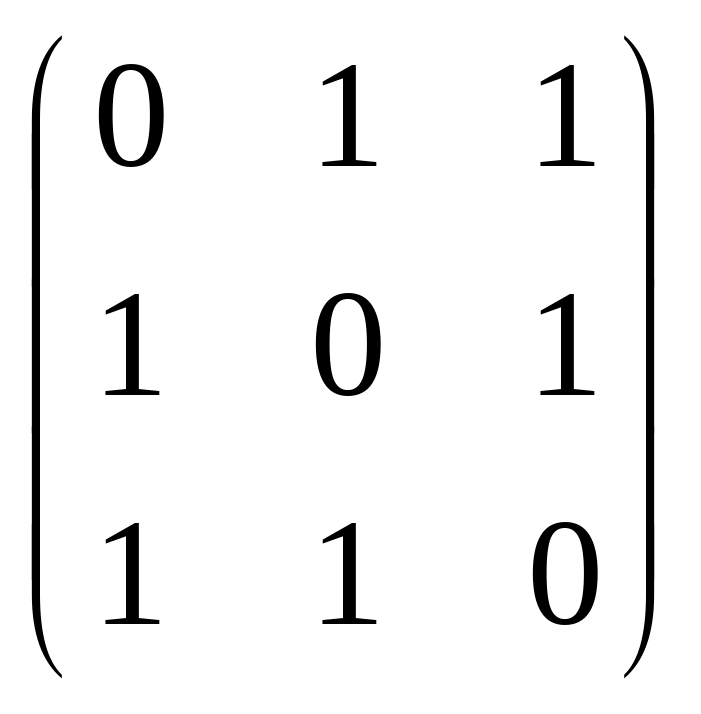
А=
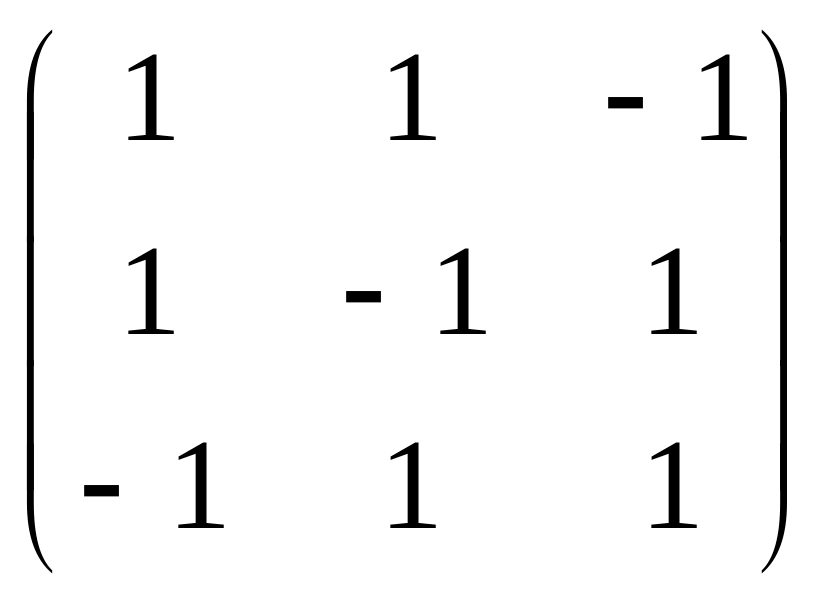 ;
В=
;
В=
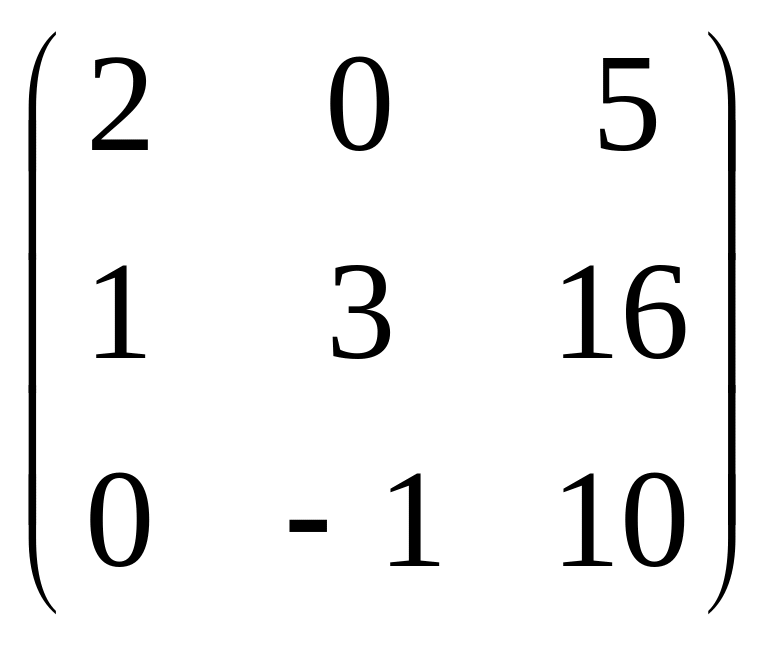
А=
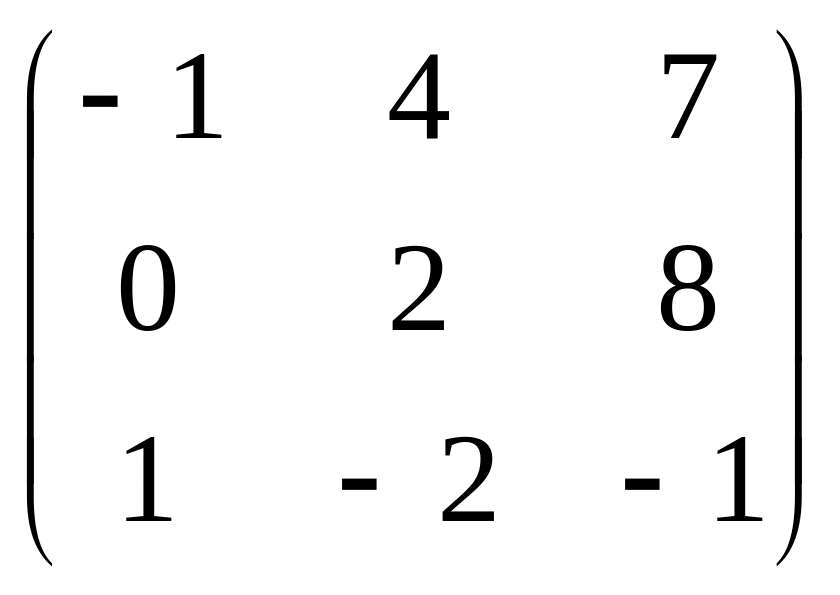 ;
В =
;
В =
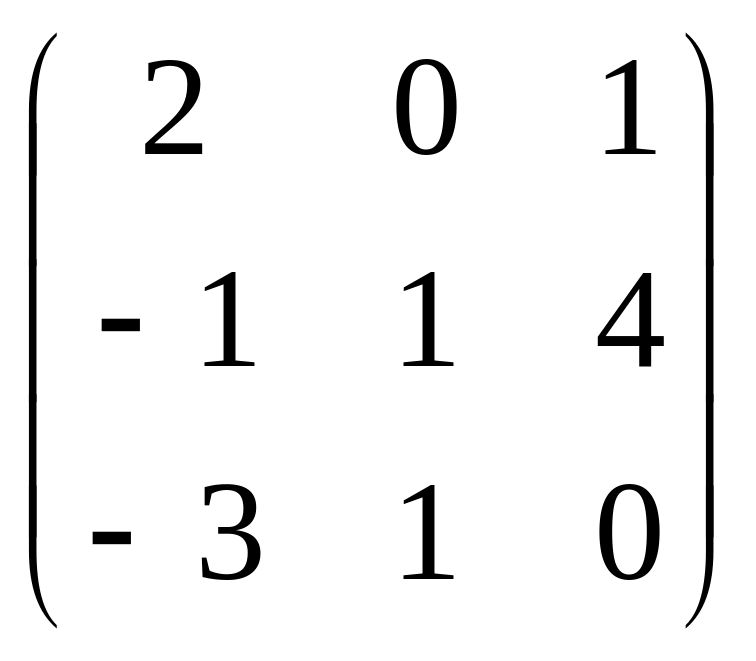
А =
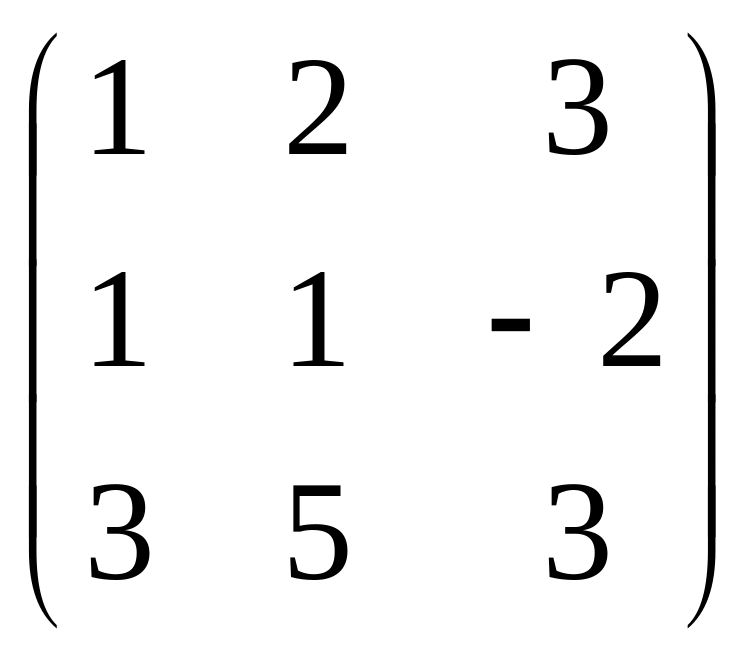 ;
В =
;
В =

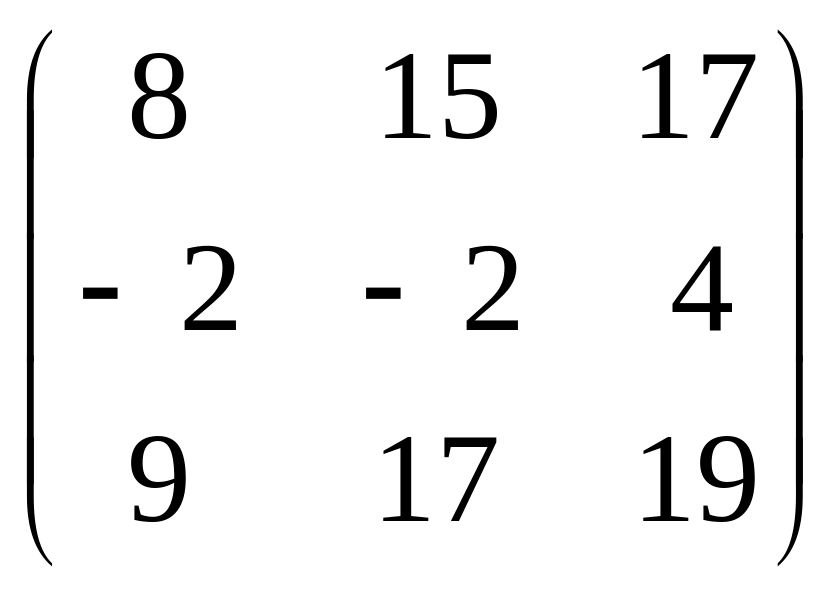
А=
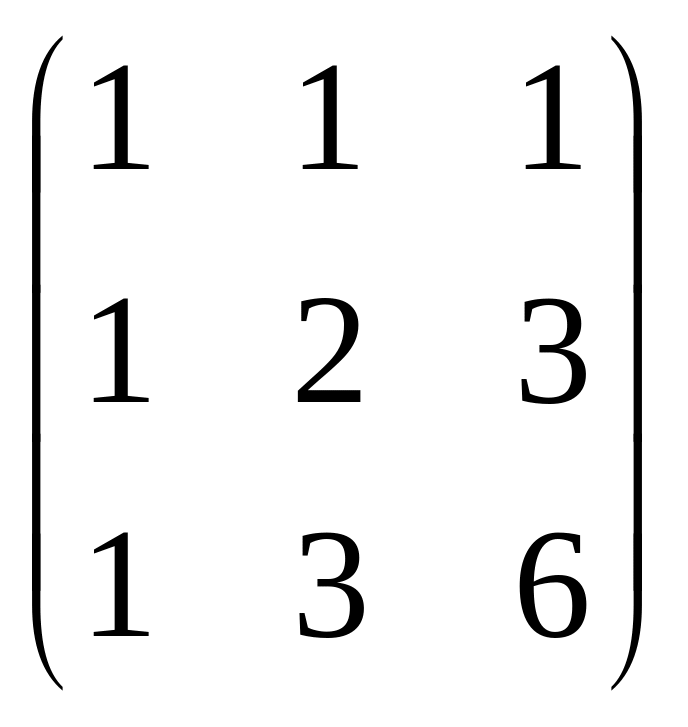 ;
В=
;
В=
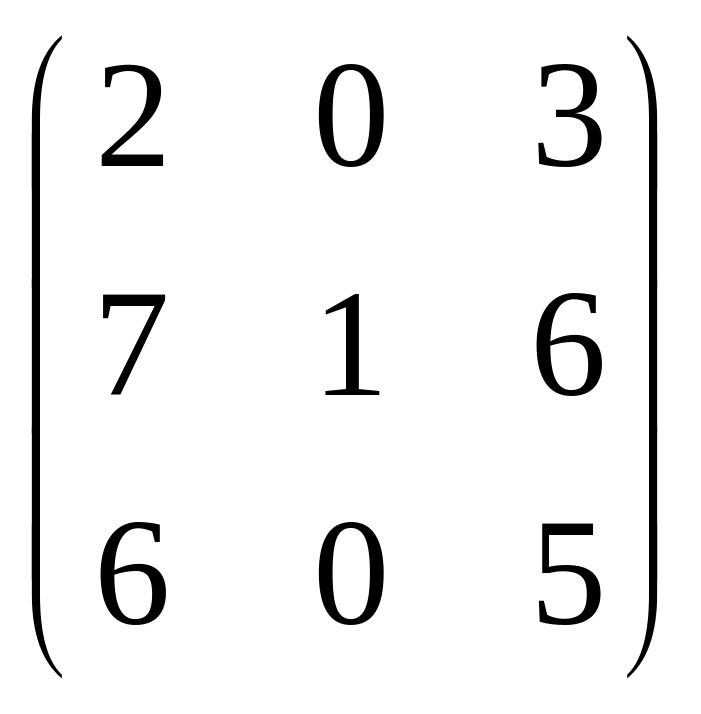
А=
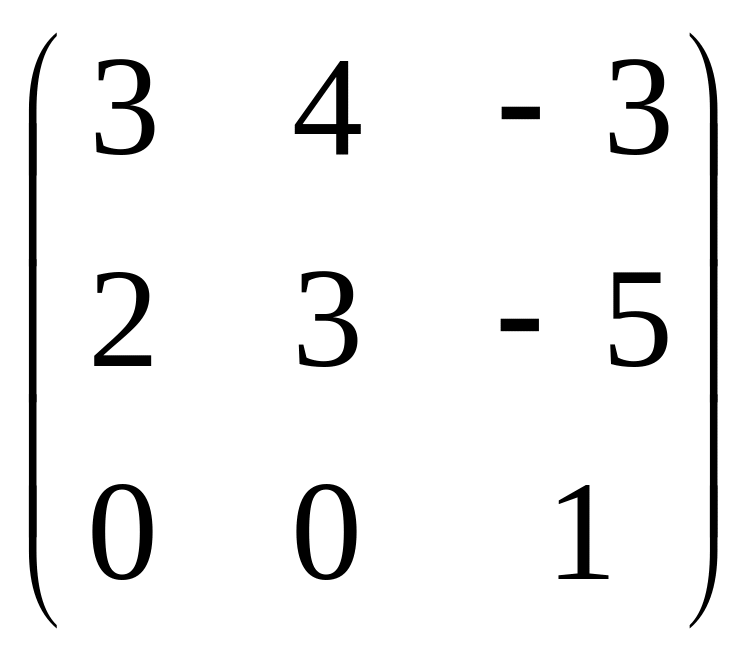 ;
В =
;
В =
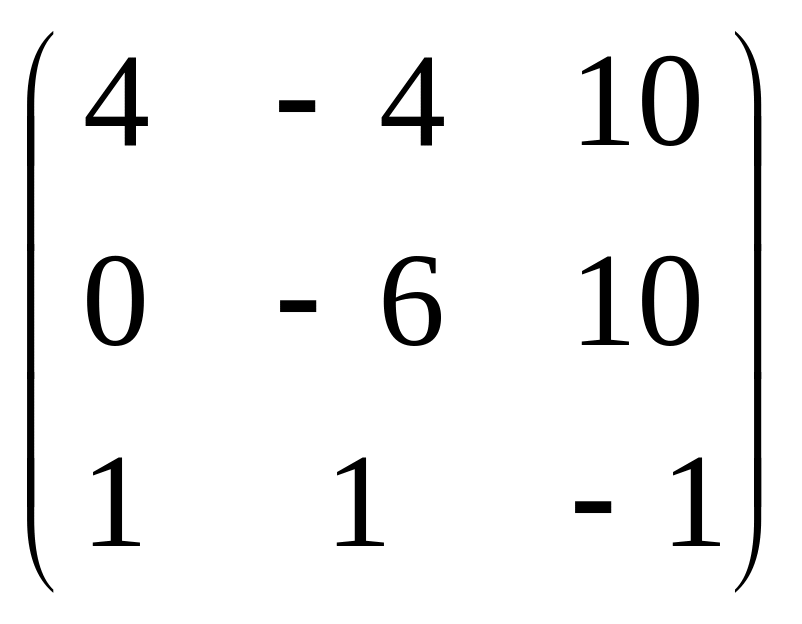
А =
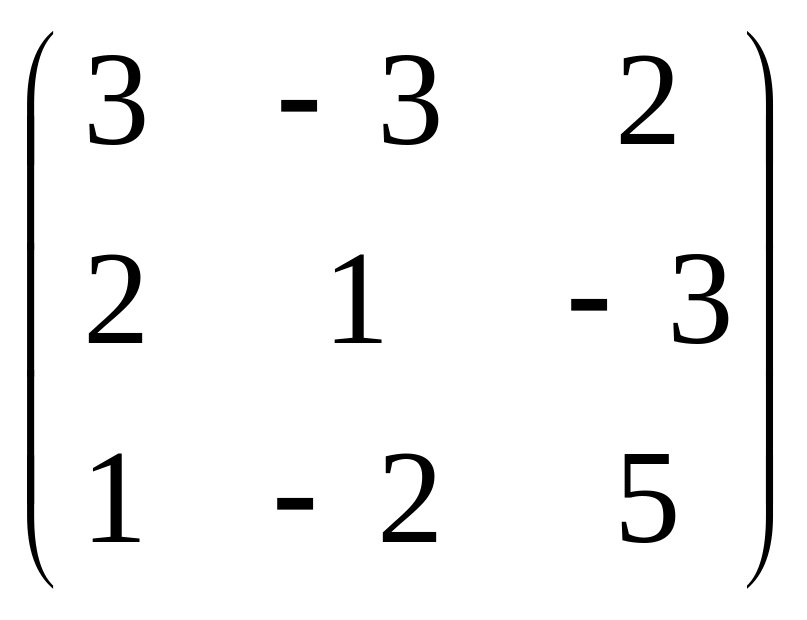 ;
В =
;
В =
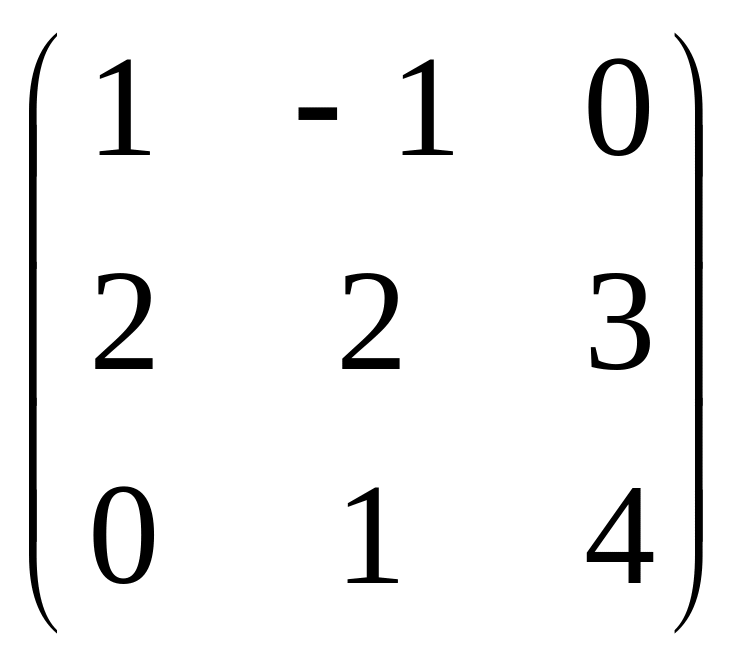
А=
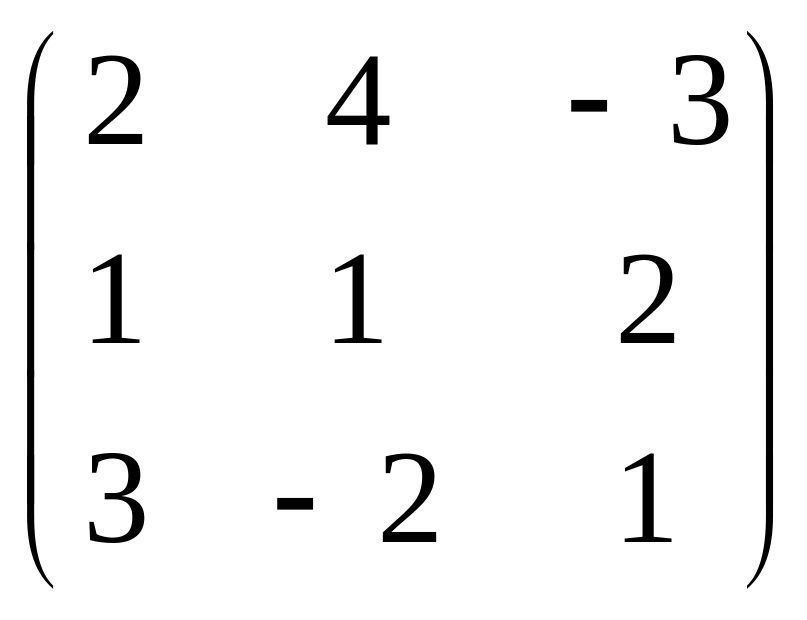 ;
В=
;
В=
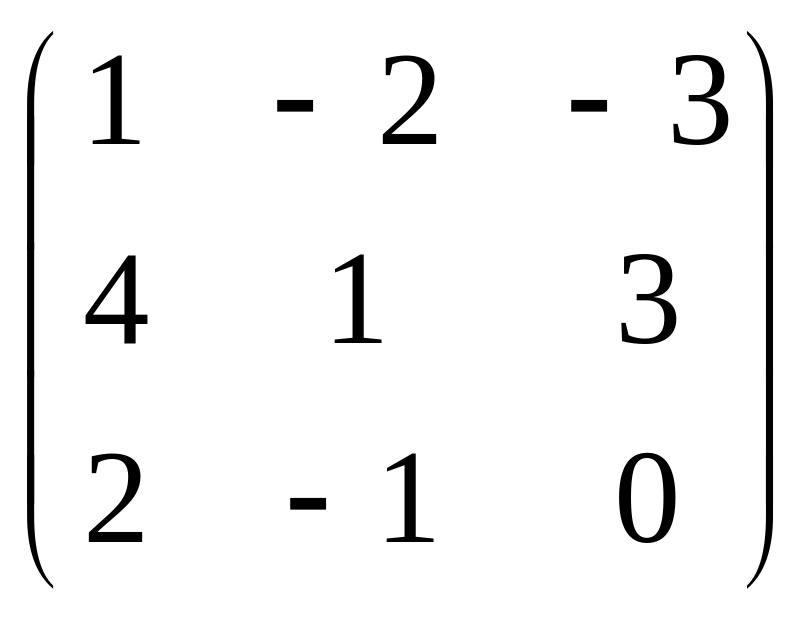
А=
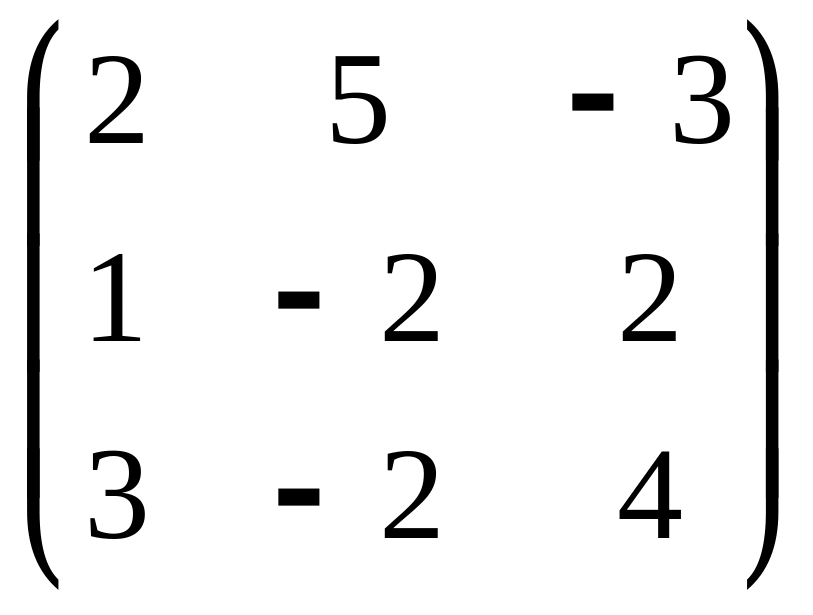 ;
В=
;
В=
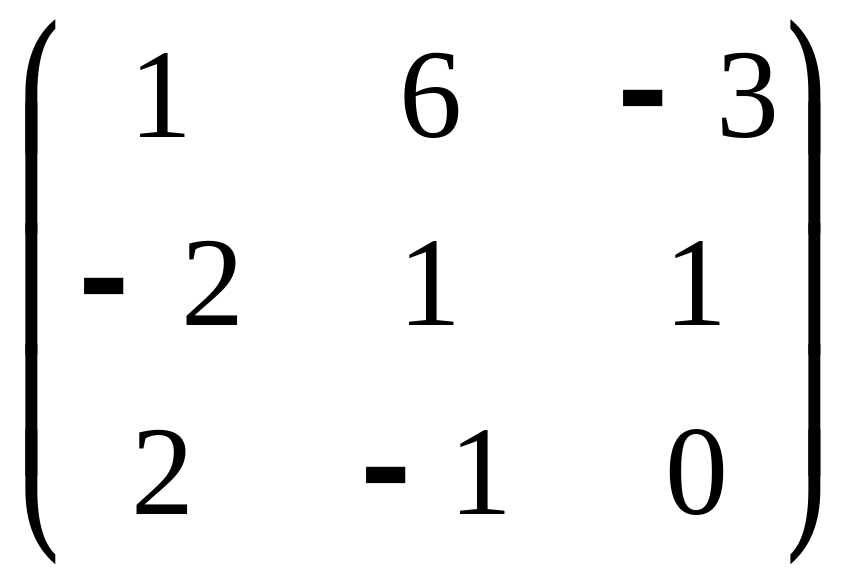
А=
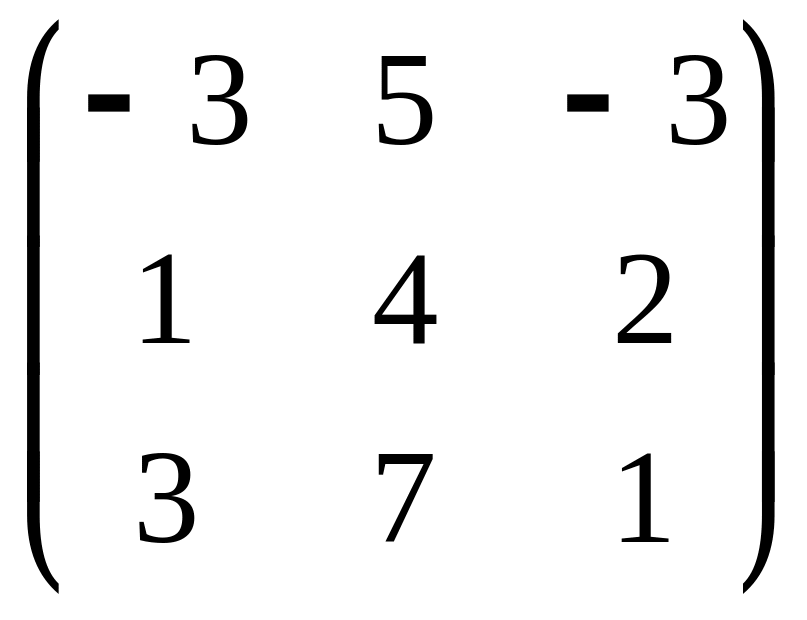 ;
В=
;
В=
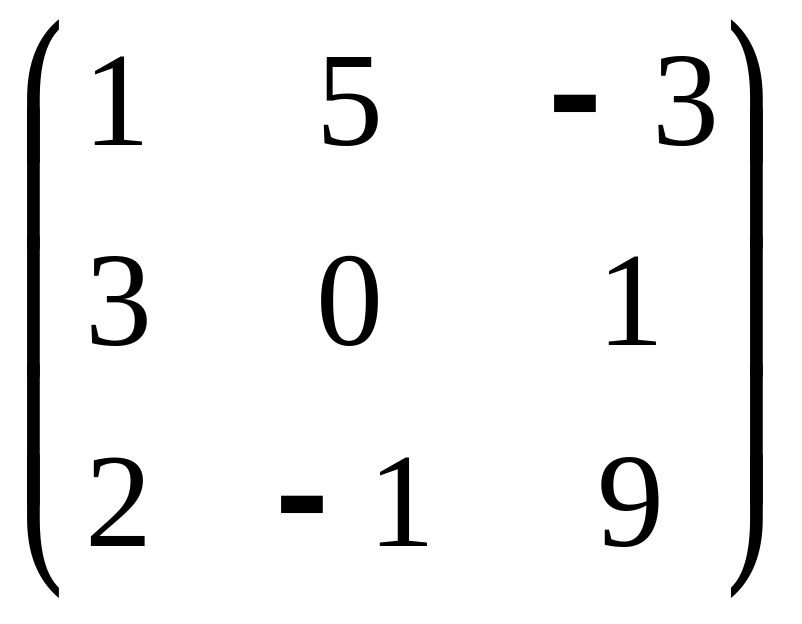
А=
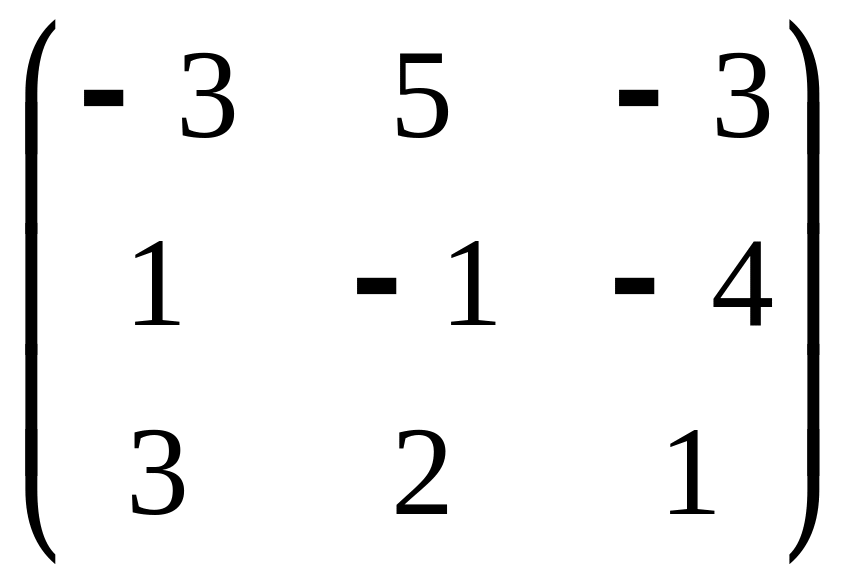 ;
В=
;
В=