Векторная алгебра

Пример 1. В пирамиде даны декартовы координаты точек вершин . Найти: 1) координаты векторов ; 2)определить длины рёбер ; 3)найти угол между рёбрами и ; 4) вычислить площадь грани ; 5) вычислить объём пирамиды .

Решение

1. найдём координаты векторов по формулам координат вектора, заданного двумя точками, получим

2. определим длины рёбер , по формуле

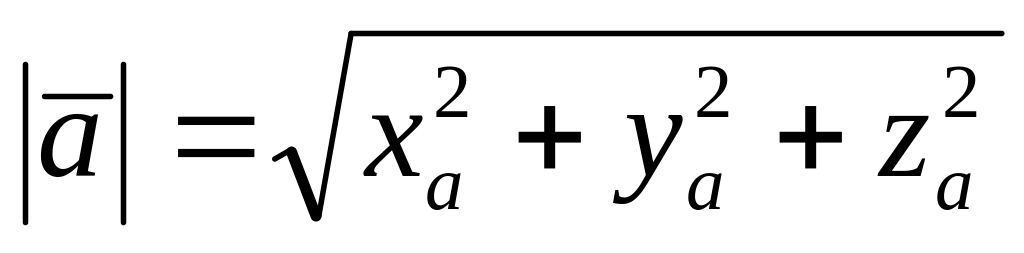
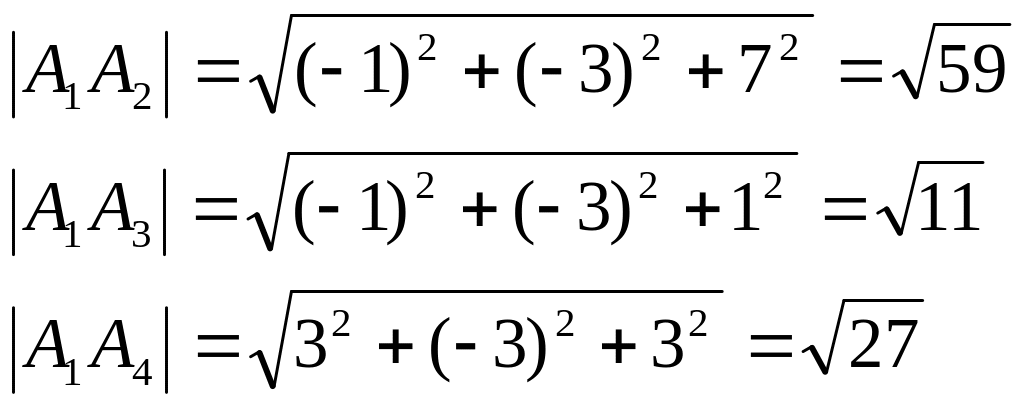
3. найдём угол между рёбрами и , используя формулу

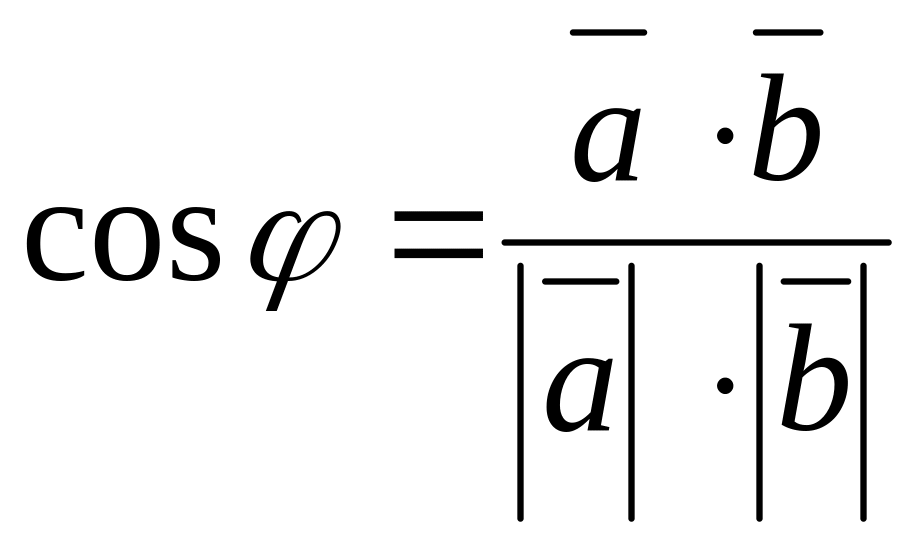
4. вычислим площадь грани по формуле 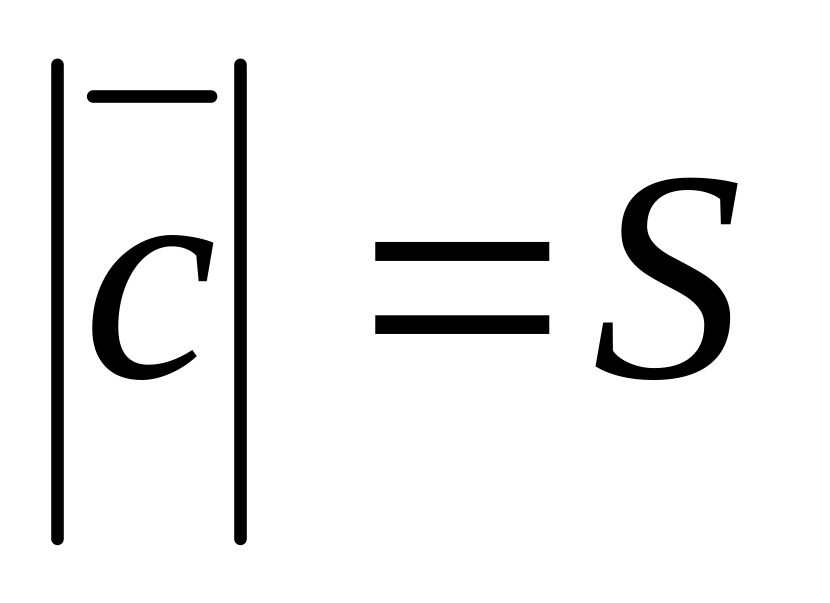- площади параллелограмма, построенного на векторах .

Вектор вычисляется по формуле :

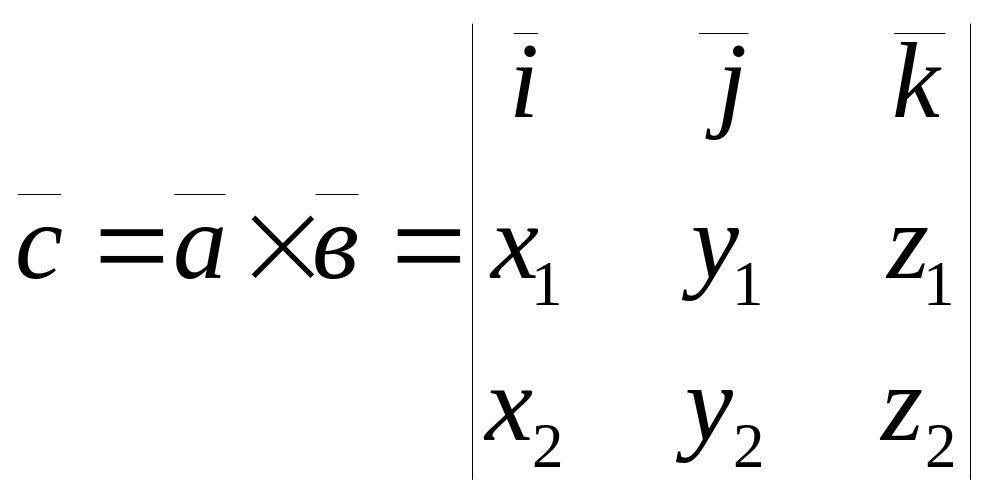5. вычислим объём пирамиды , используя смешанное произведение векторов по формуле

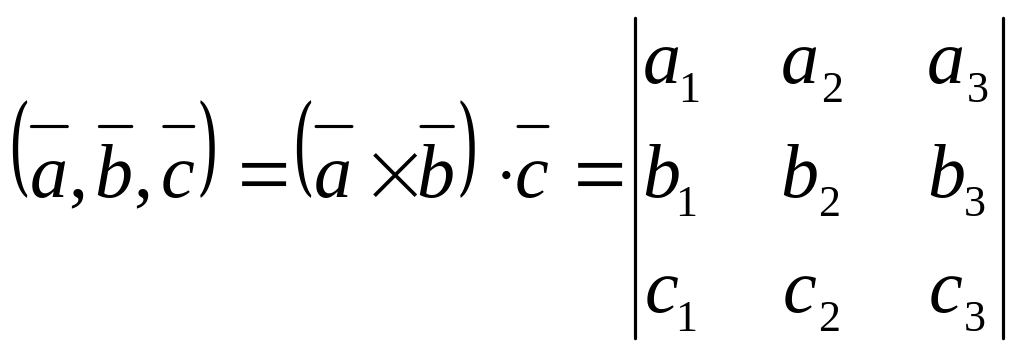
, откуда

объем пирамиды

Ответ: 1)

2) длины рёбер

3)угол между рёбрами и :

4)площадь грани :

5)объём пирамиды :

Пример 2. Даны векторы . Показать, что векторы образуют базис и найти координаты вектора в этом базисе.

Решение.

Проверим, образуют ли векторы базис, для этого используем формулу

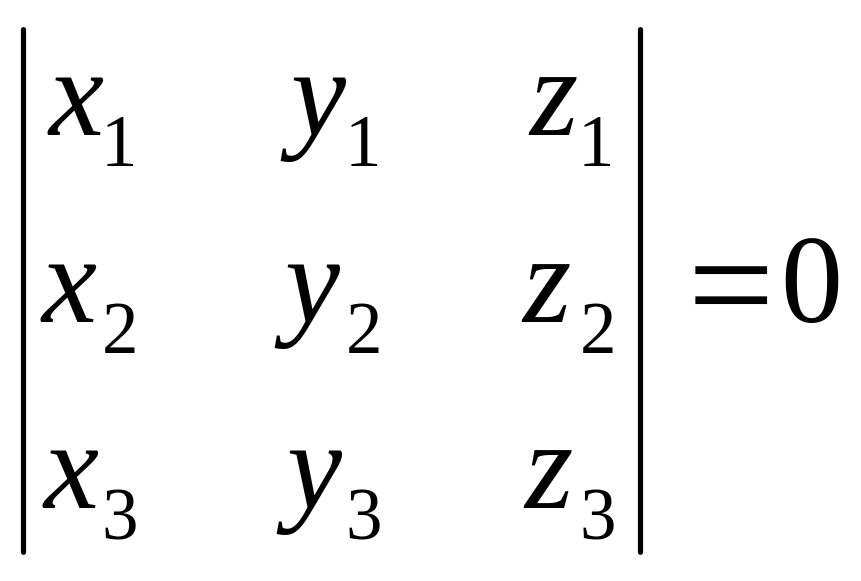
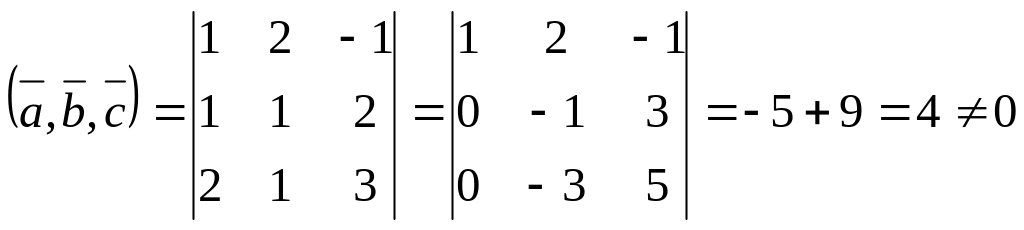- векторы образуют базис

т.е. .

Записав координаты векторов в столбцы, представим разложение вектора в виде: 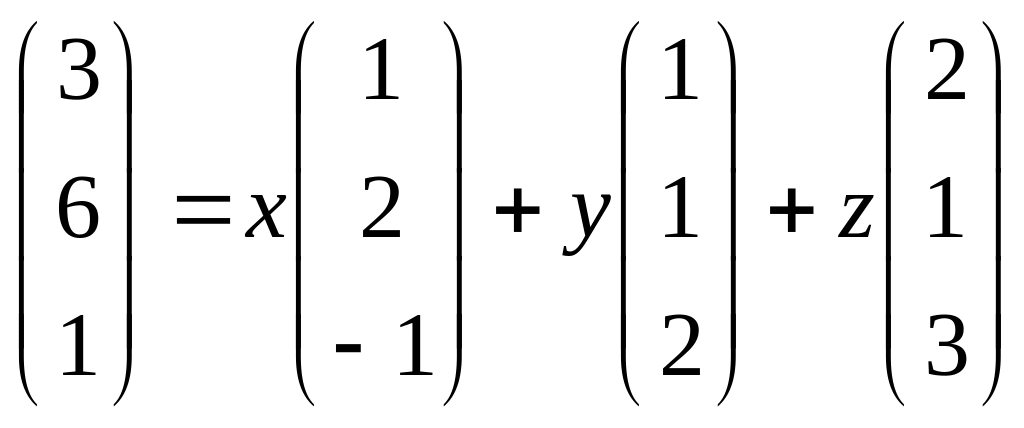. Получим систему трёх линейных уравнений с тремя неизвестными x,y,z. 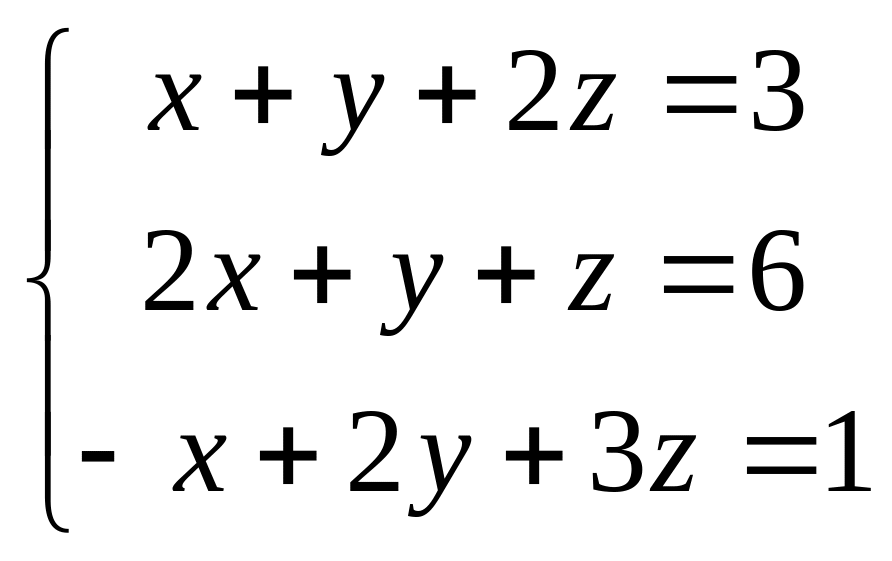. Найдем решение системы любым методом, например, методом Гаусса.

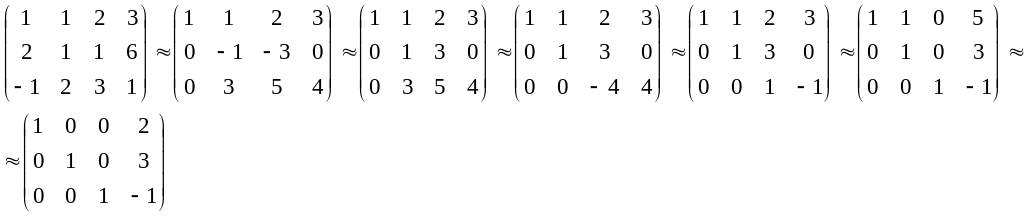
Получили x=2, y=3, z=-1, тогда .

Ответ:

Пример 3. Даны координаты трёх точек . Требуется: 1) записать векторы и в системе орт; 2) найти площадь треугольника построенного на векторах и .

Решение.

1. Для записи векторов и в системе орт воспользуемся формулой:

2. Для нахождения площади треугольника, построенного на векторах и , воспользуемся свойством векторного произведения векторов: - площади параллелограмма, построенного на векторах и площадь треугольника, построенного на векторах и равна

Вектор вычисляется как векторное произведение

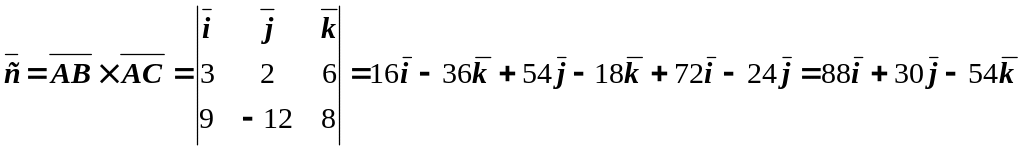
Ответ: 1)

2)

Линейная алгебра

Пример 1. Найти матрицу , если

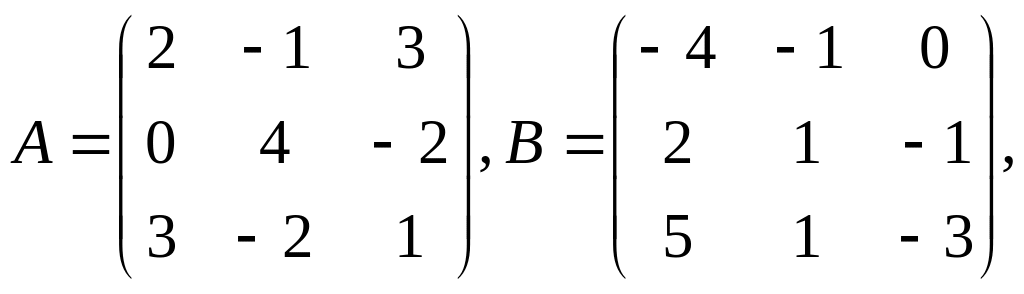
Решение.

Найдём произведение матриц, используя формулу (4):

Н айдём сумму матриц, используя формулу (2):

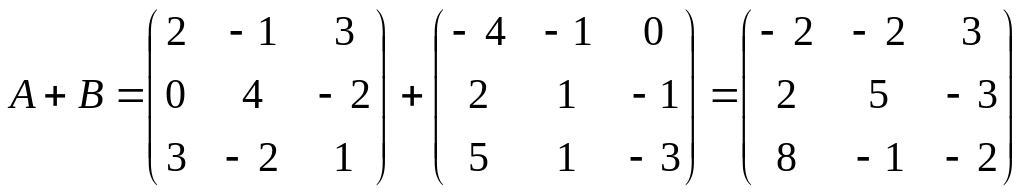
Найдём произведение матрицы на число, используя формулу (3):

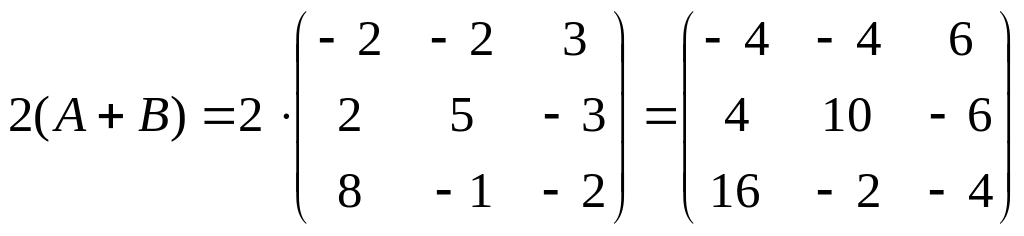
Теперь найдём разность матриц:

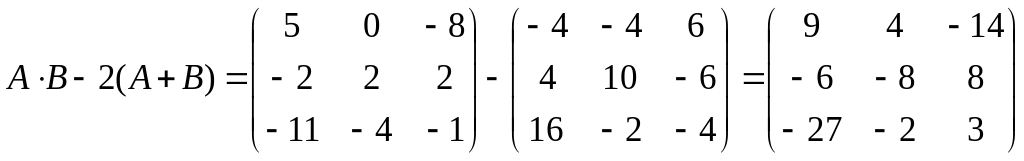
Ответ

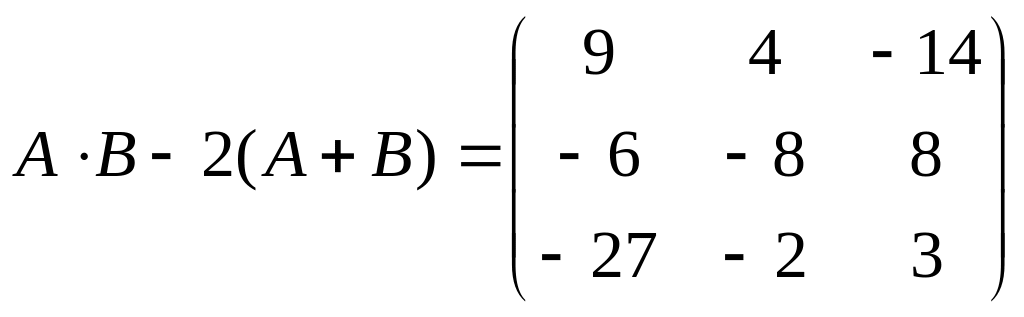
Пример 2. Найти определитель четвёртого порядка

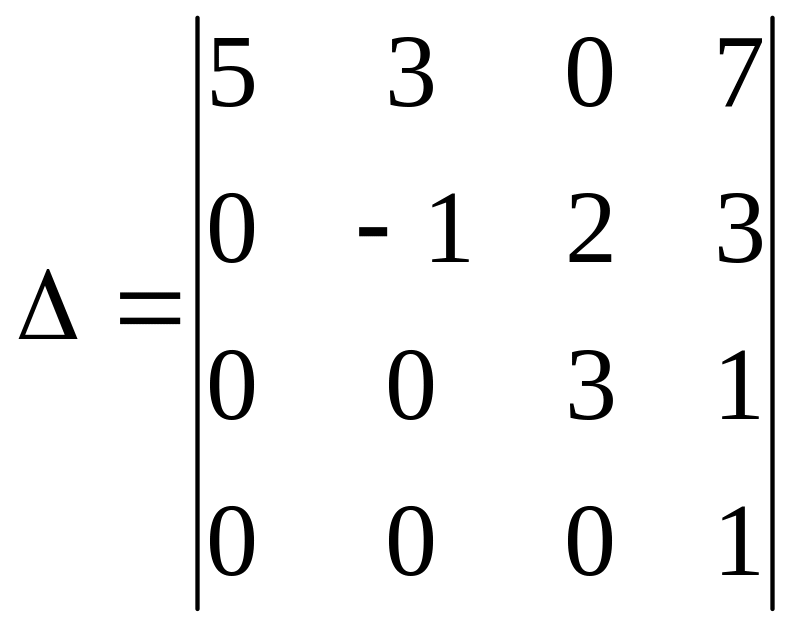
Решение.

Используем теорему Лапласа и сделаем разложение по 4-ой строке

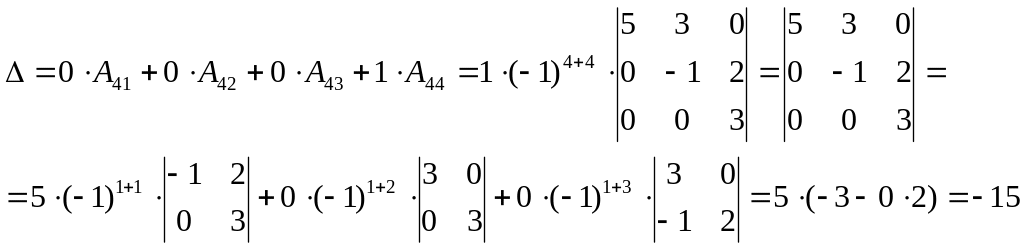
Ответ:

Пример 3. Вычислить определитель, используя свойства определителя

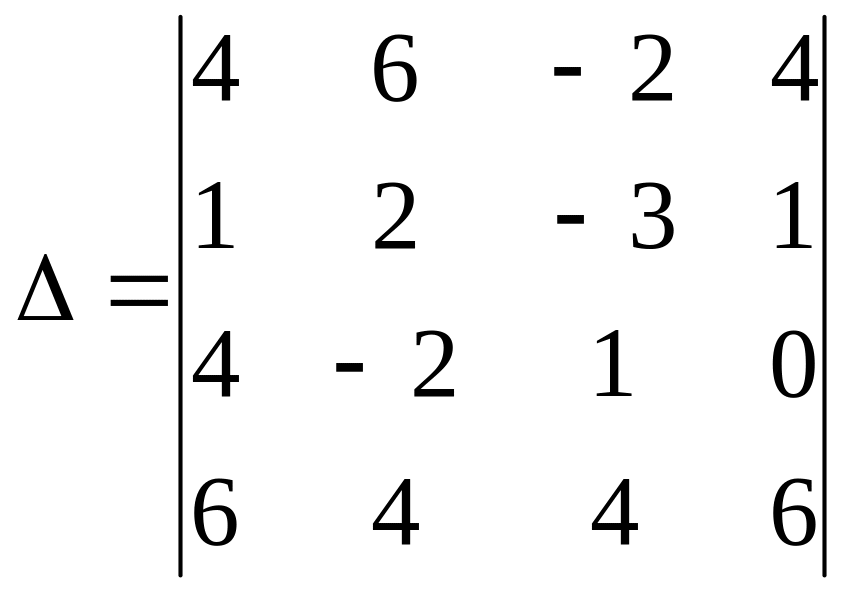
Решение.

Преобразуем определитель так, чтобы в 3-ей строке все элементы, кроме а₃₃=1, были нулями. Для этого оставим без изменения 3-й столбец и 4-ый столбец (т.к. элемент а₃₄=0). Чтобы на месте а₃₁=4 получить 0, надо элементы третьего столбца умножить на (-4) и сложить с соответствующими элементами 1-го столбца. Чтобы получить на месте а₃₂=-2 нуль, элементы 3-го столбца умножим на 2 и сложить со 2-ым столбцом:

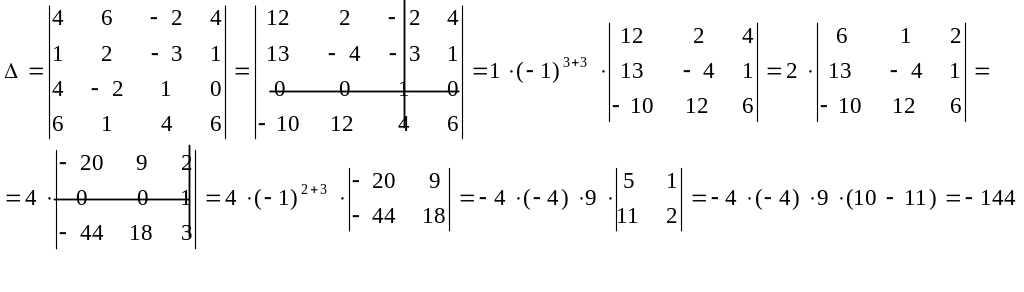
Ответ:

Пример 4. Найти обратную матрицу для матрицы

Решение:

1) Найдем определитель матрицы

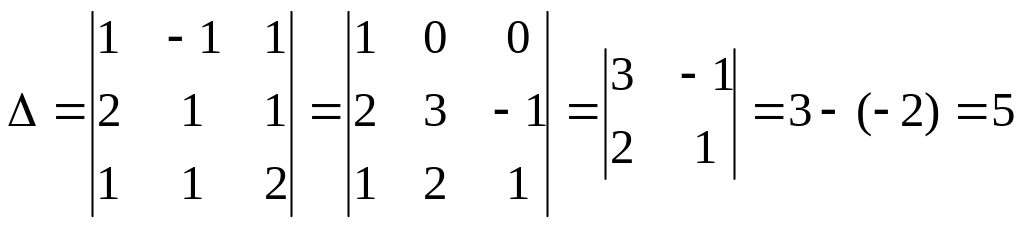
т.к. , то матрица А невырожденная, т.е. существует обратная матрица.

2) Найдем алгебраические дополнения

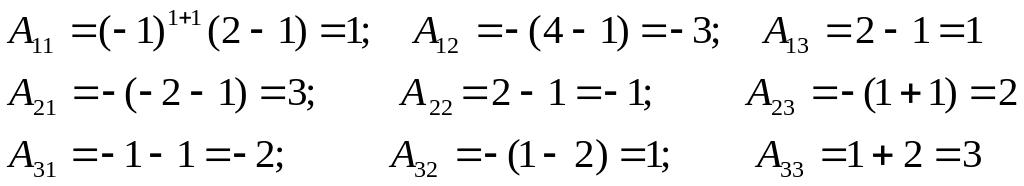
3) Составим обратную матрицу

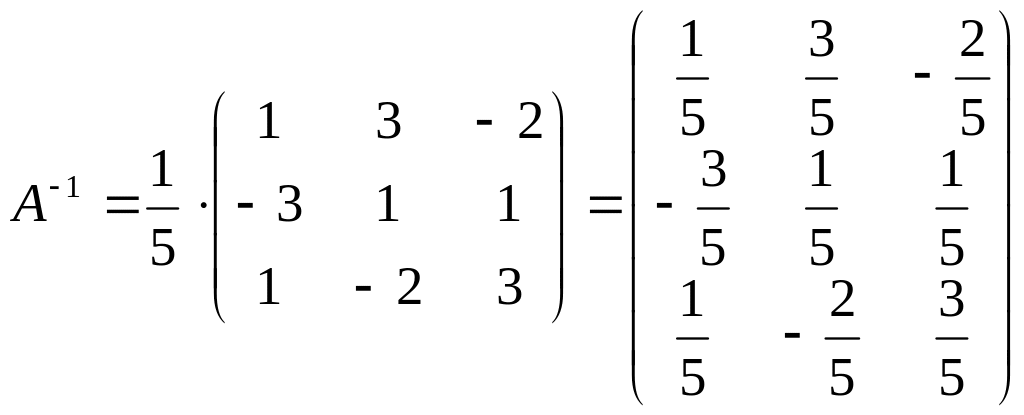
4) Проверим вычисления А^-1*А=А*А^-1=Е

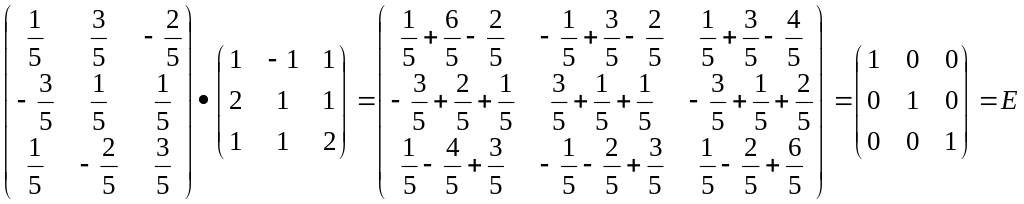
Ответ:

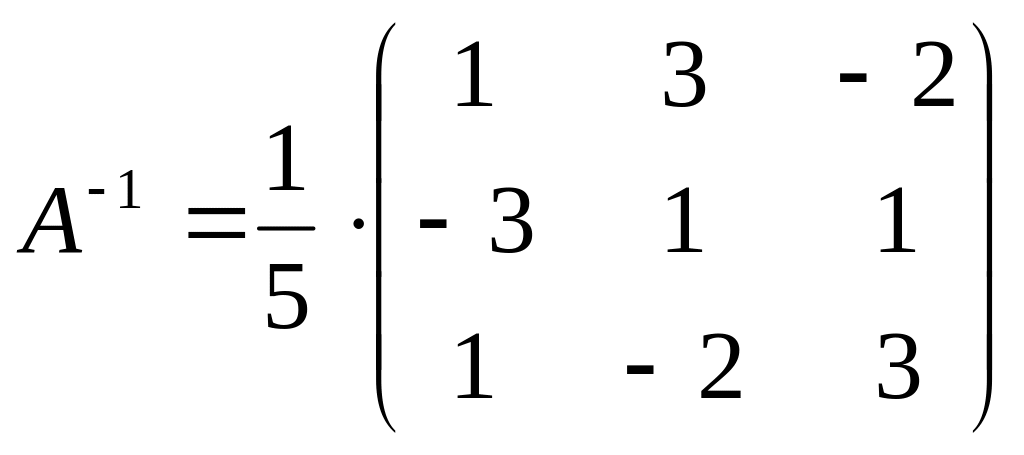
Пример 5. Найти решение системы уравнений методами: 1)Крамера; 2) обратной матрицы; 3) Гаусса.

1) Решение методом Крамера

Для решения заданной системы найдём определитель :

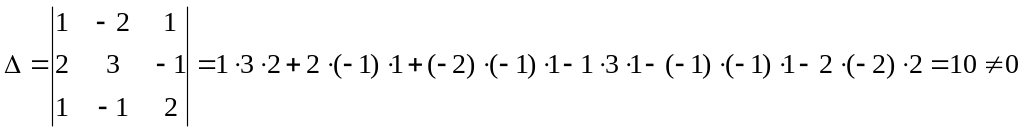
Значит, эта система имеет единственное решение найти которое можно методом Крамера, для этого найдём определители по формулам (15):

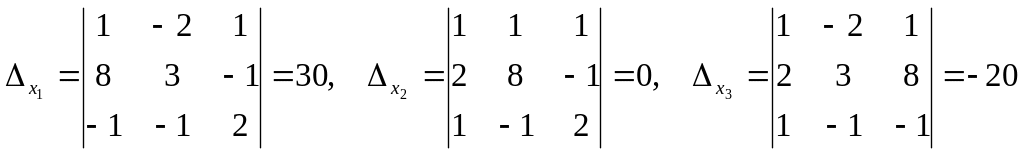
теперь найдём решения по формулам (16):

, т.е.

2) Решение методом обратной матрицы

Обозначим через А – матрицу коэффициентов при неизвестных; Х - вектор столбец неизвестных; Н – вектор столбец свободных членов:

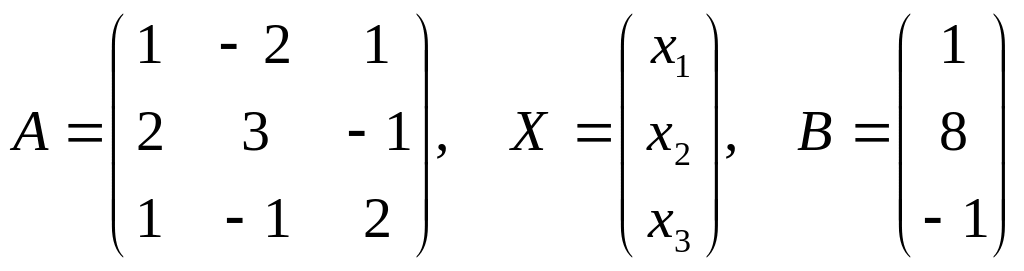
Для нахождения решения системы уравнений необходимо вычислить обратную матрицу .

Найдём сначала определитель системы.

- следовательно матрица А имеет обратную матрицу , найдём алгебраические дополнения по формуле (8):

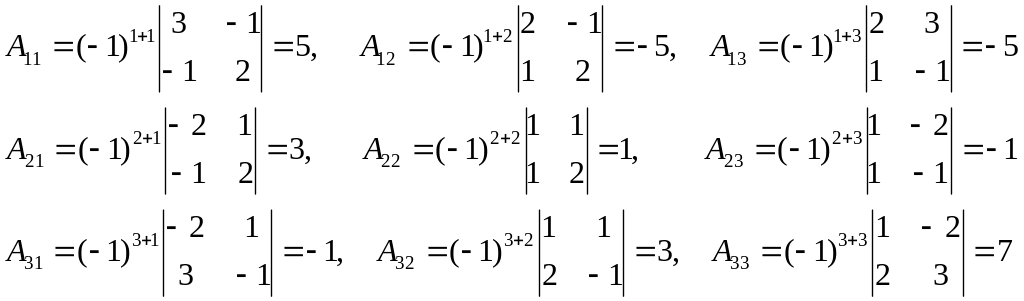
Составим обратную матрицу, используя формулу (9):

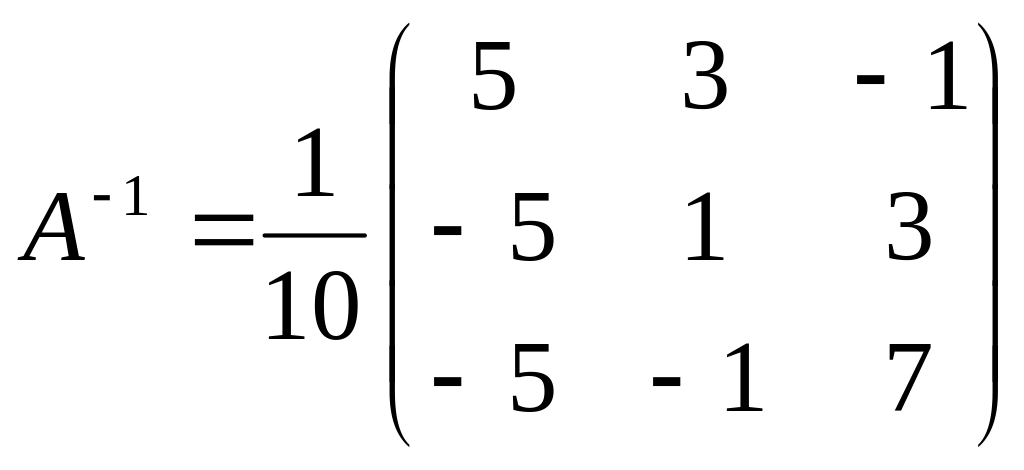
По формуле (13) находим решение данной системы уравнений в матричной форме:

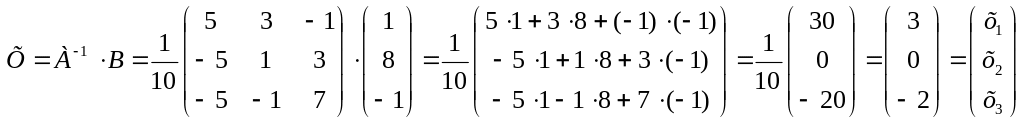
Отсюда

3) Решение методом Гаусса.

Рассмотрим исходную систему уравнений

Запишем расширенную матрицу системы

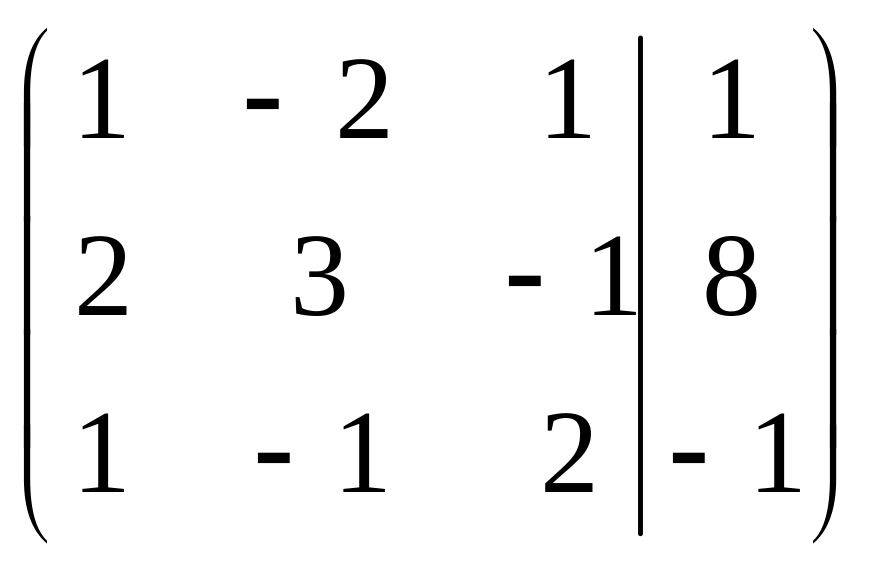
Используя элементарные преобразования над строками, приведём её к треугольному виду

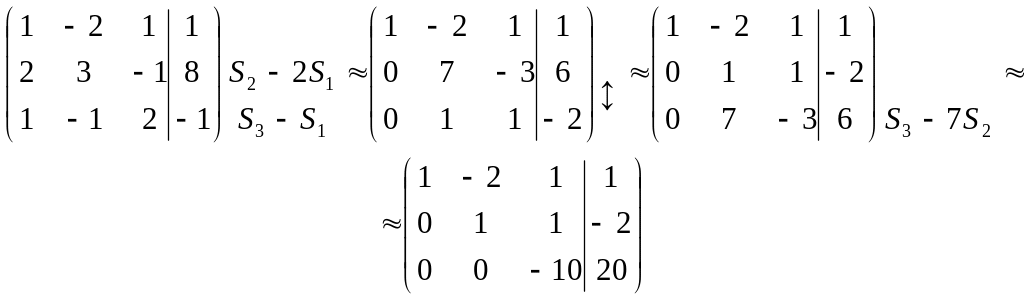
Получили матрицу треугольного вида, теперь запишем уравнение, соответствующее третьей строке матрицы:

запишем уравнение, соответствующее второй строке матрицы:

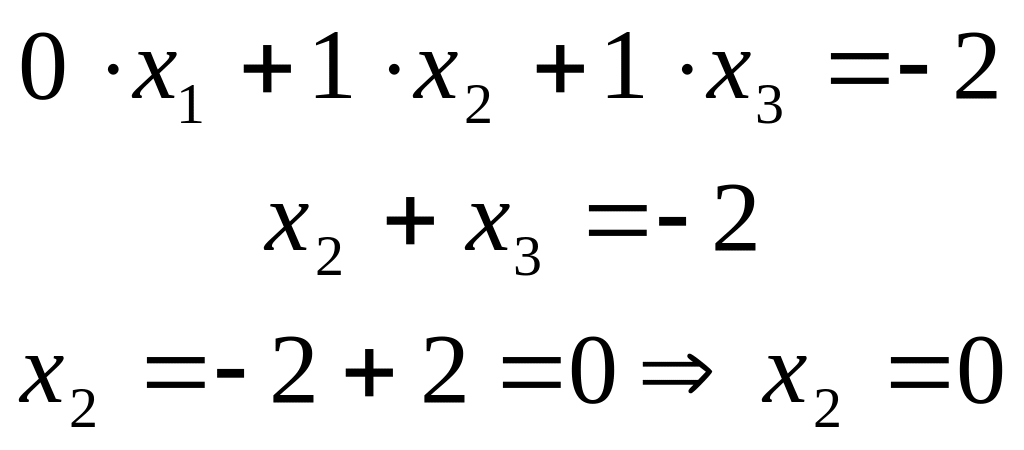
запишем уравнение, соответствующее первой строке матрицы:

таким образом получили:

Ответ: