74. Теорема Руше

Теорема вытекает из принципа ограниченности. (шпора 73)

Теорема Руше:

Пусть ф-ции f(z) и – анна-тичны на кусочно-гладком замкнутом контуре Г и внутри его, причём в точках этой кривой вытекает условие:

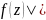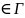| |< | , z тогда внутри Г сумма f(z)+ имеет столько же нулей, что и ф-ция f(z).

75. Теорема Гурвица

Теорема Гурвица:

Если { }- пос-ность ф-ций, анали-ских в некоторой области G, равномерно сходится в этой области к некоторой ф-ции f(z) ,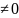

То для любой кусочно-гладкой замкнутой кривой 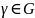вместе со своей внутренностью и не проходящей через нули ф-ции f(z),

можно указать такое число N=N( ), что при любом n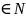 каждая из ф-ций будет иметь внутри одно и тоже число нулей, равное числу нулей ф-ции f(z), лежащей внутри этой кривой.

76. Целые функции

Опр.

Ф-ция f(z) – однозначна и аналитическая во всей компактной плоскости z наз. целой ф-цией

Согласно этому опред. целая ф-ция не имеет особых точек в конечной плоскости. Сле-но, она может иметь особую точку z= .

Пусть f(z) –целая функция. Тогда разложение

f(z)=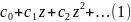

имеет место во всех точках комплекстной пло-сти Z.

Возможны следующие частные случаи

1)z= - устронимая особая точка ф-ции f(z).

Тогда разложение (1) примет вид

f(z)=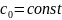

2) z= - полюс n-го порядка , тогда (1) примет вид

f(z)=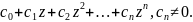

В этом случаи f(z)- целая рациональная ф-ция степени n.

3) z= - существенная особая точка, тогда (1) примет вид

f(z)= , где должно быть бесконечное мно-ство коэ-тов отличных от нуля. В этом случаи ф-цию f(z) называется целой трансцендентной ф-цией.

77. Разложение целой функции в произведение.

Можно показать, что каждой целой функции имеющей 0 существует разложения на множители аналогично разложению многочленов на множители. Чтобы подчеркнуть аналогию перепишем разложение многочлена на множители в форме несколько отличной отобщеупотребительной.

Пусть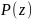 - многочлен, 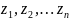- его нули отличные от начало координат, среди них могут быть и равные, что соответствует равным корням.

Пусть является нулём кратност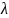и , если 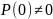, то .

Тогда многочлен можно представить в виде следующего произведения:

,

где .

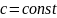Для сравнения возьмём целую функцию 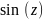имеющую простые нули: .

Если расположить нули отличные от начала координат в порядке неубывающих модулей, положив: , , , 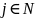то можно доказать формулу:

.

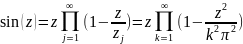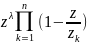Однако, в общем случае такой простой формулы не получается. Дело в том, что если – целая функция с нулями кратности и , то произведение может расходится.

Чтобы справится с этой трудностью, Вейерштрасс ввёл в произведение дополнительный множитель вида:

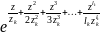, которые сами в нуль ни где не обращается, но обеспечивает сходимость произведения. Если подобрать соответствующим образам числа , то для получается формула Вейерштрасса:

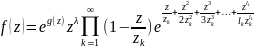
где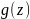 – некоторая целая функция, 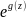– также целая функция, которая нигде не обращается в нуль.

78. Мероморфные функций.

Опр.ф-ция, которую можно представить в виде частного двух целых ф-ций наз мероморфной ф-цией

Теорема.

Если меро-ная ф-ция имеет лишь конечное число полюсов в конечной плоскости и точка бесконечность является для неё у.о.т. или полюсом, то эта ф-ция рациональная.