6. Взаимодействие тел, сила, масса. Второй закон Ньютона. Виды силовых взаимодействий. Силы упругости, трения, тяготения.

Взаимодействие между телами осуществляется полями. Тело массы М возбуждает в окружающем пространстве гравитационное поле, которое проявляется в виде действия на тело массы m силы (частный случай – молекулярные силы; наблюдается слипание образцов).

Cила – мера интенсивности взаимодействия тел, в результате которого они получают ускорения или деформируются. В СИ- Н

Масса – универсальная мера материи, мера инертности тела, мера гравитации. Измеряется в СИ – КГ.

2 закон Ньютона: вектор ускорения прямо пропорционален геометрической сумме векторов всех сил, действующих на м. т. и обратно пропорционален массе этого тела.

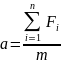
Силы, действующие между материальными точками (телами) данной системы, называют внутренними силами (f).

Силы, действующие на тела системы со стороны других тел, не входящих в данную систему, называют внешними силами (F).

Замкнутой системой называют систему, на которую действие внешних сил компенсировано

Сила упругости- это сила возникающая при упругой деформации тел..

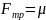mg

Сила притяжения двух м. т. прямо пропорциональна произведению масс

взаимодействующих м. т. и обратно пропорциональна квадрату расстояния между ними:

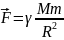
Второй закон Ньютона является законом поступательного движения в инерциальных системах отсчета, т. е.

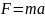
7. Третий закон Ньютона. Импульс. Изолированная система. Закон сохранения импульса.

Систему тел называет изолированной, если на тела системы не действуют силы.

Закон сохранения импульса: в замкнутой системе тел векторая сумма импульсов тел входящих в систему, есть величина постоянная.

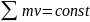
Импульсом тела называют произведением его массы на скорость.

3 закон Ньютона: силы, с которыми взаимодействуют тела, равны по величине и противоположны по направлению. Линия действия сил лежит на одной прямой, соединяющей центры масс этих тел.

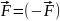
В замкнутой системе тел векторная сумма импульсов этих тел, входящих в систему, есть величина постоянная.

Измеряется в СИ – кг м/с

8. Неинерциальные системы отсчета. Силы инерции в поступательных и во вращательных неинерциальных системах отсчета.

Неинерциальными системами отсчета называют системы отсчета,

которые движутся относительно инерциальных систем отсчета, с ускорением.

1. Силы инерции действуют только в неинерциальных системах отсчета.

2. Силы инерции вызваны не взаимодействием тел, а ускоренным движением системы отсчета.

3. К силам инерции не применим третий закон Ньютона, так как нет взаимодействующих тел.

4. Если некоторая система тел (м. т.) находится в неинерциальной системе отсчета, то силы инерции являются внешними силами, следовательно, системы не являются замкнутыми и поэтому не выполняются законы сохранения.

5. В неинерциальных системах отсчета силы инерции действуют точно также, как и силы взаимодействия тел, например, космонавт, весьма реально ощущает силу инерции, прижимающую его к креслу корабля, после старта ракеты на активном участке полета.

6. Силы инерции прямо пропорциональны массе тел. Поэтому в поле сил инерции все тела движутся с одинаковыми ускорениями.

9. Центр масс. Теорема о движении центра масс.

Центр масс – это геометрическая точка, характеризующая распределение масс в теле.

Центр масс механической системы движется как материальная точка с массой, равной массе всей системы, к которой приложено.

10. Движение тела переменной массы. Уравнение Мещерского.

Пусть в t=0 ракета начинает движение в СИ связанной с Землей 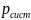=0

Через dt :

U – относительная скорость отделяющейся массы.

Масса ракеты : m≠dm

Скорость ракеты : d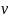

Масса отделившейся части : dm

Скорость отделившейся части :

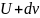
Изменение импульса системы :

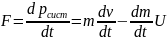
Уравнение Мещерского:

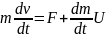
11. Движение в центральном поле сил. Законы Кеплера и закон всемирного тяготения.( дописать движение в центральном поле сил)

12. Консервативные и неконсервативные силы. Работа консервативных сил. Потенциальная энергия.

( работа консервативных сил)

13. Связь между силой и потенциальной энергией. Потенциальные энергии силы тяжести, силы упругости и силы гравитационного взаимодействия. ( силу тяжести)

14. Механическая работа и кинетическая энергия. Механическая энергия системы тел. Закон сохранения механической энергии.

15. Соударение двух тел. Абсолютно упругий и абсолютно неупругий удар.

16. Момент импульса и момент силы относительно неподвижного начала. Уравнение моментов.

17. Уравнение моментов. Закон сохранения момента импульса.

18. Момент импульса и момент силы относительно неподвижной оси. Уравнение динамики вращательного движения относительно неподвижной оси.

Если тело (или м. т. А) вращается относительно полюса 0

произвольным образом, то оно может повернуться вокруг оси, совпадающей

с направлением вектора момента силы относительно полюса, лежащего на

этой оси (рис. 5).

Проекция вектора момента силы на произвольную ось, проходящую

через полюс, равна проекции на эту ось векторного произведения радиус-

вектора r и вектора силы F относительно полюса 0, лежащего на этой оси:

Момент импульса тела относительно оси

Проекция момента импульса твердого тела на произвольную ось,

проходящую через полюс 0, равна проекции на эту ось векторного

произведения радиус-вектора и вектора импульса тела относительно того же

полюса 0, лежащего на этой оси, т. е.

Если у твердого тела ось симметрии совпадает с осью вращения, то векторы

моментов импульсов для м. т., лежащих по разные стороны от оси вращения при суммировании дают результирующий вектор момента импульса L , лежащий на оси вращения

направление которого определяется правилом правого винта и совпадает с направлением вектора угловой скорости, т. е.

 основным уравнением динамики для твёрдого тела, вращающегося вокруг неподвижной оси.

Здесь ε = — угловое ускорение вращающегося тела.