25. Гармонический осциллятор. Уравнение динамики гармонических колебаний. Примеры гармонических осцилляторов: пружинный, физический и математический маятники.

Гармонический осциллятор – колебательная система, совершающая гармонические  колебания, то есть показатели которой периодически повторяются во времени.

Уравнение динамики гармонического колебания:

Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.

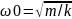
Физический маятник – это тело, совершающие под действием силы тяжести колебания вокруг горизонтальной оси, не проходящей через центр масс

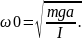. T0=2п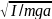

Математический маятник – частный случай физического. Тело, подвешенное на нити, можно считать МТ.

Возьмем физический и математический маятники. Меняя длину нити математического маятника l, добьемся, чтобы периоды колебаний совпадали. Такую длину l называют приведенной длиной физического маятника. Обозначим ее L.

2п

L=I/ma

26. Затухающие колебания. Коэффициент затухания, время релаксации. Логарифмический декремент затухания.

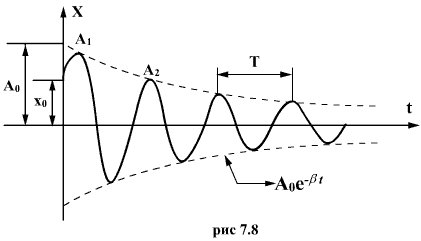
Затухающие колебания - колебания, амплитуда которых постепенно уменьшается, напр. колебания маятника, испытывающего сопротивление воздуха и трение в подвесе. 

Колебания называются затухающими, если убыль энергии физической системы не восполняется в процессе ее колебательного движения.

Коэффициент затухания - количественная характеристика сопротивления колеблющейся системы колебательному движению.

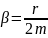
Временем релаксации называют промежуток времени, за который амплитуда затухающих колебаний уменьшается в е раз (е – основание натуральных логарифмов).

отсюда         

Логарифмическим декрементом затухания называют натуральный логарифм отношения амплитуды в данный момент времени к амплитуде колебания спустя период.

Логарифмический декремент затухания прямо пропорционален произведению коэффициента затухания и периоду затухающих колебаний.

27. Вынужденные колебания. Амплитуда и фаза вынужденных колебаний. Резонанс. Резонансные характеристики осциллятора (добротность,избирательность).

Вынужденные колебания — колебания, происходящие под воздействием внешних периодических сил.

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону:  .

Амплитуда вынужденных колебаний зависит от соотношения между круговой частотой вынуждающей силы и собственной частотой физической системы и от коэффициента затухания. Амплитуда колебаний неограниченно возрастает при ω= ω0.

Результирующая амплитуда

Амплитуда вынужденных колебаний зависит от соотношения между круговой частотой вынуждающей силы и собственной частотой физической системы и от коэффициента затухания.

Начальная фаза результирующего колебания :

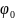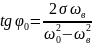
Сдвиг фаз между смещением пружинного маятника и вынуждающей силой зависит сложным образом от

коэффициента затухания, частоты вынуждающей силы и собственной частоты физической системы. Механическим резонансом называют явление резкого возрастания амплитуды колебаний, когда круговая частота вынужденных колебаний ωв совпадает с собственной круговой частотой физической системы. Явление резонанса очень широко используется в науке и технике. Например, для обнаружения весьма слабых колебаний. Поскольку амплитуда вынужденных колебаний зависит от вынуждающей частоты и имеет резонансный максимум при ωв = ωo, то поглощаемая энергия, наоборот, имеет резонансный минимум не пик, а «провал» или «яму».

Физическую величину, характеризующую потери энергии при затухающих колебаниях, называют добротностью. Чем больше добротность, тем медленнее затухают колебания осциллятора. Добротность определяет частотную избирательность резонансных систем.

Как известно, энергия прямо пропорциональна квадрату амплитуды, тогда формулу можно представить в следующем виде:

, где

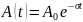
При малых колебаниях физической системы (малы сопротивление, потери энергии) добротность можно найти при Т→ Т0 по формуле:

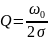
Избирательностью осциллятора называется его способность выделять из различных сигналов, отличающихся по частоте, сигнал принимаемой станции. Так как передаваемое сообщение имеет определенную полосу частот, другой не менее важной функцией приемника является прием сигнала высокой частоты со всеми его боковыми частотами, т. е. одновременный прием определенной полосы частот. При этом необходимо, чтобы соотношения между амплитудами составляющих спектра сигнала оставались без изменений.