21. Гидростатика. Закон Паскаля. Закон Архимеда. Основное уравнение гидростатики.

Гидростатика  - раздел гидромеханики, изучающая законы равновесия жидкости, которые находится в состоянии абсолютного или относительного покоя и равновесия тел, погруженных в жидкости при условии, что отсутствуют перемещения частиц жидкости друг относительно друга.

Основной задачей гидростатики является определение (описание) скалярного поля давления в жидкости, находящейся в покое. Это давление описывается уравнением:

 , где  - Векторное поле единичных массовых сил (сила, действующая на единицу массы жидкости);  - плотность (удельная масса) жидкости; p - давление.

Это соотношение справедливо как для несжимаемой (идеальной) жидкости, так и для сжимаемой (реальной) жидкости и газов.

Основное уравнение гидростатики где р1 – абсолютное давление, Па; рo – давление на свободную поверхность, Па; ρ – плотность, кг/м3; g – ускорение свободного падения, м/с2; h – глубина погружения, м.

Уравнение является фундаментальным и называется основным уравнением гидростатики и показывает, что гидростатическое давление в любой точке покоящейся капельной жидкости изменяется в зависимости только от вертикальной координаты этой точки.

Величина р1 называется абсолютным р(абс) гидростатическим давлением в точке 1. Оно равно абсолютному давлению на свободной поверхности ро плюс гидростатическое (или весовое) давление ρgh , обусловленное весом самой жидкости. Внешнее давление, оказанное на свободную поверхность замкнутого объема несжимаемой жидкости, передается жидкостью одинаково всем ее точкам по всем направлениям. Это закон Паскаля. На этом законе основан принцип работы гидравлических машин.

Закон Паскаля описывается формулой давления:

p=F/S,

где  p – это давление, F – приложенная сила, S– площадь сосуда.

Закон Архимеда: на тело, погружённое в жидкости (или газы), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда:

где   — плотность жидкости (газа),   — ускорение свободного падения, а   — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плаваетна поверхности или равномерно движется вверх или вниз, то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.

22. Стационарное движение идеальной жидкости. Уравнение Бернулли.

Идеальная жидкость — воображаемая несжимаемая жидкость, лишенная вязкости и теплопроводности. В идеальной жидкости отсутствует внутреннее трение, т. е. нет касательных напряжений между двумя соседними слоями, она непрерывна и не имеет структуры. Такая идеализация допустима во многих случаях течения, рассматриваемых в гидроаэродинамике, и дает хорошее описание реальных течений жидкостей и газов на достаточном удалении от омываемых твердых поверхностей.

В идеальной жидкости могут существовать только силы нормального давления, которые можно вычислить с помощью уравнения состояния Р=f(r, T).

Работа, совершаемая силами давления при перемещении некоторой массы жидкости:

A=A1-A2=

Эта работа ровна приращению   полной энергии выделенной части жидкости.

Изменение полной энергии

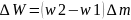
W1,W2-полные энергии приходящейся на единицу массы жидкости до и после перемещения соответственно

Вдоль одной и той же линии тока, если течение идеальной жидкости стационарно, величина     постоянна:   ­– уравнение Бернулли.

   складывается из потенциальной и кинетической энергии –  . Учитывая это мы, можем переписать уравнение Бернулли в таком виде  .